Производная степенной функции.

Формула производной степенной функции имеет вид 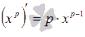, где показатель степени p – любое действительное число.

Следует рассмотреть два случая: при положительных x и отрицательных x.

Сначала будем полагать . В этом случае . Выполним логарифмирование равенства по основанию e и применим свойство логарифма:

Пришли к неявно заданной функции. Находим ее производную:

Пример.

Найти производные функций .

Решение.

Первую и третью функцию приведем к табличному виду , используя свойства степени, и применим формулу производной степенной функции:

Производная показательной функции.

Вывод формулы производной приведем на основе определения:

Пришли к неопределенности. Для ее раскрытия введем новую переменную 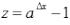, причем

при 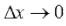. Тогда . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.

Выполним подстановку в исходный предел:

Если вспомнить второй замечательный предел, то придем к формуле производной показательной функции:

Пример.

Найти производные показательных функций .

Решение.

Воспользуемся доказанной выше формулой производной показательной функции из таблицы и свойствами логарифма.