1. Что понимается под нечеткой логикой?

2. Определение нечеткого множества. Способы задания нечеткого множества.

3.Основные способы задания функций принадлежности.

4.Понятие лингвистической переменной. Примеры

5.Основные операции над нечеткими множествами и способы их определении.

6.Что понимается под S- нормой и Т- нормой. Примеры заданий этих функций

7. Что понимается под нечетким алгоритмом? Структура реализации нечеткого алгоритма.

8. Механизм нечеткого вывода. (Механизм логического вывода)

9. Что понимается под дефаззификацией? Назовите основные методы дефаззификации?

10. Метод нечеткого вывода «максимума – минимума»

11. Метод нечеткого вывода «максимума – произведения»

12. Принципы нечеткого управления. Структурная схема системы нечеткого управления.

13. Процедура синтеза нечеткого регулятора (НР).

14. Нечеткий регулятор Такаги – Сугено. В чем его отличие от нечеткого регулятора Мамдани?

15. Блок – схемы систем управления с использованием нечетких регулирующих систем.

16. Методы реализации нечетких алгоритмов в системах управления.

1. Что понимается под нечеткой логикой?

Принцип несовместимости Лотфи Заде: «Чем сложнее система, тем менее мы способны дать точные и имеющие практические суждения о ее поведении. Для систем, сложность которых превосходит некоторый пороговый уровень, точность и практический смысл становится исключающее друг друга характеристиками».

Лингвистическая переменная – ключевое понятие нечеткой системы.

Суть подхода нечеткой логики:

1. Использование лингвистических переменных вместо обычных числовых, либо в дополнение к ним.

2. Простые отношения между переменными описывается с помощью нечетких высказываний

3. Сложные отношения описываются нечеткими алгоритмами.

2. Определение нечеткого множества. Способы задания нечеткого множества.

Нечеткие множества (лингвистические переменные) – термин был введен Л.Заде:

х– объектная переменная

А – множество взрослых людей

μ(х)= {1, х≥18

{0, х< 18

Заданное таким образом множество пар А= {(х, μ(х)) | х є Х} называется нечетким (размытым) множеством.

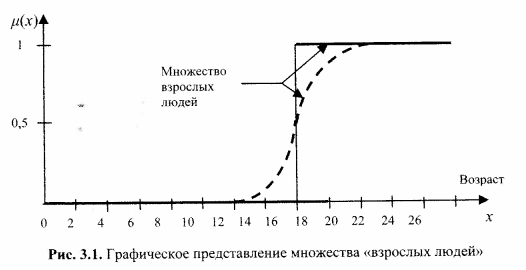
А= (х(μ(х));хєХ)

А= (16,02)

А= (20,08)

х	14	16	18	20	22
μ(х)	0	0,2	0,5	0,8	1

Процесс перехода от четкого, измеренного значения к его нечеткой интерпретации называется фазификация (fuzzy).

Ф-ии принадлежности μ(х) может рассматриваться как субъективная вероятность или коэф-т уверенности эксперимента в том, что элемент принадлежит к множеству.

Ключевым элементом нечеткой логики является лингвистическая переменная. Конкретное значение лингв. переменной подвергается субъективной оценки эксперта.

3.Основные способы задания функций принадлежности.

Задать нечеткое множество соответствующее определенному темпу лингв. переменной – это задать область определения числовой переменной х, ф-ии принадлежности μ(х) по множеству.

- табличный

- графический

- аналитически

4.Понятие лингвистической переменной. Примеры.

Переменные, значениями которых являются термы (слова, фразы, предложения), выраженные на естественном языке, называют лингвистическим переменным.

Рассмотрим в качестве примера лингвистическую переменную «Яркость». Будем полагать, что различные значения физической переменной х (яркость, в кд/м²) м.б. охарактеризованы набором из 5 нечетких подмножеств (значений лингвистической переменной): «Очень темно», «Темно», «Светло», «Очень светло».

На рисунке показаны ф-ии принадлежности для каждого из этих подмножест.

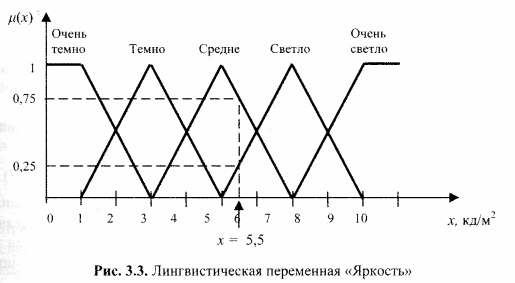
Допустим, что фактическое значение яркости равно 5,5 кд/м² . Тогда, в соответствии с рис., это значение относится одновременно к двум термам (подмножествам) – «Среднее» и «Светло» - со степенями принадлежности μ_средне(5,5)=0,75 и μ_светло(5,5)=0,25 соответственно.

5.Основные операции над нечеткими множествами и способы их определении.

Операции над нечеткими множествами:

1)Эквивалентность: μ_А(х)=μ_В(х) (рис.3.4 а)

2)Включение – нечеткое множество А содержится в нечетком множестве В: μ_А(х)≤μ_В(х)

3)Объединение (дизъюнкция, ИЛИ) : μ_AUB=max(μ_А(х);μ_В(х)) (рис.3.4 б)

4)Пересечение (И): μ_A∩B=min(μ_А(х);μ_В(х)) (рис.3.4 в)

5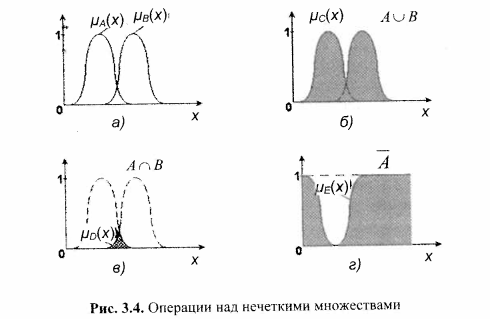 ) Дополнение: ¬А=1 – μ(х) (рис.3.4 г)

6)Алгебраические произведение (реализации):

1.μ_А*В = μ_А(х) * μ_В(х) – умножение

2.μ_А=В = μ_А(х)+μ_В(х) – μ_А(х)* μ_В(х) – сложение

7)Концентрации: μ_{con A}= μ²(х) –термин «очень»

8)Растяжение: DIL(A)=A^0,5

μ _{DIL A}(x)= - операция «довольно»

U – S – норма – операция объединения

∩ - Т – норма – операция пересечения

9)Нечеткие алгоритмы – понятие ввел Л.Заде.