16.Выпуклость кривой. Точка перегиба

Говорят, что кривая обращена в точке выпуклостью кверху (книзу), если существует окрестность такая, что для всех точек этой окрестности касательная к кривой в точке (т. е. в точке, имеющей абсциссу ) расположена выше (ниже) самой кривой (на рис. 55 в точке кривая обращена выпуклостью книзу, в точке - кверху). Вместо слов «выпукла кверху (книзу)» употребляются слова «вогнута книзу (кверху)». Говорят, что точка есть точка перегиба кривой , если при переходе через точка кривой (имеющая абсциссу ) переходит с одной стороны касательной на другую (на рис. 55 точка - точка перегиба). Иначе говоря, существует достаточно малое такое, что для всех кривая находится с одной стороны касательной в , а для всех - с другой.

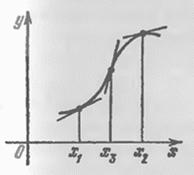
Рис. 55

Для функции

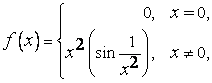
ось пересекает и касается графика функции в точке и не есть точка перегиба.

Теорема 1. Если функция имеет в точке вторую непрерывную производную и , то кривая обращена в выпуклостью книзу (кверху.) Доказательство. Разлагаем в окрестности по формуле Тейлора

,

.

Запишем уравнение касательной к нашей кривой в точке, имеющей абсциссу :

.

Тогда превышение кривой над касательной к ней в точке равно

.

Таким образом, остаток равен величине превышения кривой над касательной к ней в точке . В силу непрерывности , если , то и для , принадлежащих достаточно малой окрестности точки , а потому, очевидно, и для любого отличного от значения , принадлежащего к указанной окрестности.

Значит, график функции лежит выше касательной, и кривая обращена в точке выпуклостью книзу.

Аналогично, если , то для любого отличного от значения , принадлежащего к некоторой окрестности точки , т. е. график функции лежит ниже касательной и кривая обращена в выпуклостью кверху.

Следствие. Если есть точка перегиба кривой и в ней существует вторая производная , то последняя необходимо равна нулю .

Этим пользуются на практике: при нахождении точек перегиба дважды дифференцируемой кривой , ищут их среди корней уравнения .

Достаточное условие для существования точки перегиба у кривой дается следующей теоремой.

Теорема 2. Если функция такова, что производная непрерывна в , а и , то кривая имеет в точке точку перегиба.

Доказательство. В этом случае

,

.

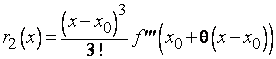В силу непрерывности в и того факта, что , следует, что сохраняет знак в некоторой окрестности точки ; он один и тот же справа и слева от точки . С другой стороны, множитель меняет знак при переходе через , а вместе с ним и величина (равная превышению точки кривой над касательной в ) меняет знак при переходе через . Это доказывает теорему.

Сформулируем более общую теорему:

Теорема 3. Пусть функция обладает следующими свойствами:

,

непрерывна в окрестности и .

Тогда, если - нечетное число, то кривая обращена выпуклостью вверх или вниз в зависимости от того, будет ли или , а если - четное, то есть точка перегиба кривой.

Доказательство основано на том, что при указанных условиях имеет место разложение по формуле Тейлора

.

В заключение заметим, что говорят также, что кривая имеет точку перегиба в точке , где производная равна или . По определению кривая называется выпуклой кверху (книзу) на отрезке , если любая дуга этой кривой с концами в точках с абсциссами , расположена не ниже (не выше) стягивающей ее хорды (рис. 56 и 57). Замечание. Если дифференцируема на , то приведенное определение выпуклости на отрезке эквивалентно следующему: кривая называется выпуклой кверху (книзу) на отрезке , если она выпукла кверху (книзу) в каждой точке интервала .

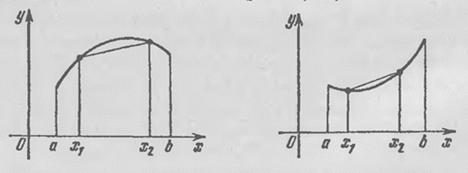
Рис. 56 Рис. 57

Теорема 4. Пусть функция непрерывна на и имеет вторую производную на . Для того чтобы кривая была выпуклой кверху (книзу) на , необходитмо и достаточно, чтобы выполнялось неравенство для всех .

Пример, что бы было понятно. Функция имеет непрерывную первую производную и вторую производную на . Поэтому хорда , стягивающая дугу кривой на , ниже синусоиды (рис. 58). Так как уравнение хорды , то мы получили неравенство

, часто употребляемое в математическом анализе.

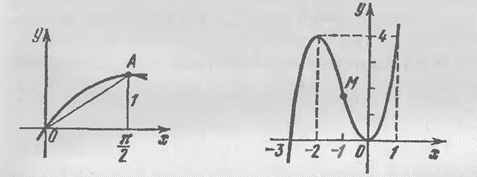
Рис. 58 Рис.59

2. при при . Так как , то в точке - перегиб. Далее при , при . Значит, график функции (рис. 59) выпуклый кверху на и выпуклый книзу на ; - точка минимума, - точка максимума.