- •Понятие функции. Основные свойства функций. Основные элементарные функции. Сложная функция. Обратная функция.
- •1)Область определения функции и область значений функции.
- •Понятие сложной функции
- •Обратная функция
- •Предел функции (определение, основные теоремы, свойства пределов).
- •Свойства пределов функции
- •Функции, непрерывные на отрезке. Основные теоремы о непрерывных функциях.
- •Первый замечательный предел
- •Второй замечательный предел
- •Дифференциал функции. Приближённые вычисления с помощью дифференциала.
- •Дифференциал функции. Опр. Дифференциал функции называется главная линейная относительно часть приращения функции, равная произведению производной на приращение независимой переменной .
- •Приближенные вычисления с помощью дифференциала.
- •Производная сложной и обратной функций.
- •Производная обратной функций.
- •Монотонность функции. Критерии возрастания и убывания функции на интервале.
- •Локальный экстремум. Достаточные критерии локальных экстремумов.
- •16.Выпуклость кривой. Точка перегиба
Приближенные вычисления с помощью дифференциала.
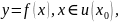 найти:
найти:
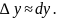
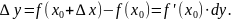
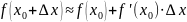
Формула для вычисления приближённого значения.
Производная сложной и обратной функций.
Производная сложной ф-ции.
Пусть
переменная
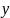 есть функция от переменной
есть функция от переменной
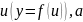 переменная
переменная
 в свою очередь есть функция от независимой
переменной
в свою очередь есть функция от независимой
переменной
 ,т.е. задана сложная
функция
,т.е. задана сложная
функция
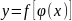 .
.
Теорема.
Если
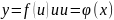 -
дифференцируемые функции от своих
аргументов, то производная сложной
функции существует и равна производной
данной функции существует по промежуточному
аргументу и умноженной на производную
самого промежуточного аргумента по
независимой переменной
,т.е.
-
дифференцируемые функции от своих
аргументов, то производная сложной
функции существует и равна производной
данной функции существует по промежуточному
аргументу и умноженной на производную
самого промежуточного аргумента по
независимой переменной
,т.е.
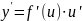 .
.
Дадим независимой переменной
приращение
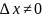 .
Тогда функции
.
Тогда функции
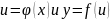 соответственно получат приглашение
соответственно получат приглашение
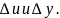
Предположим,
что
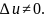 Тогда в силу дифференцируемости функции
Тогда в силу дифференцируемости функции
 можно записать
можно записать
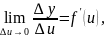
Где

На
основании теоремы о связи бесконечно
малых с пределами функций
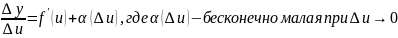 ,
откуда
,
откуда
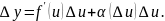
Это
равенство будет справедливо и при
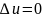 ,
если полагать, что
,
если полагать, что
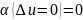 (т.е.
доопределит таким образом функцию
(т.е.
доопределит таким образом функцию
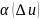 при
при

Разделив обе части равенства:
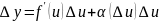 на
на
 .
.
Т.к. по условию функция
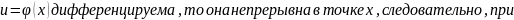
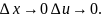
Поэтому,
переходя к пределу при
в равенстве
 получим
получим
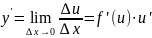 .
.
Замечание.
Если ограничиться случаями , что при
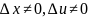 ,
доказательство теоремы можно провести
проще, исходя из очевидного равенства
,
доказательство теоремы можно провести
проще, исходя из очевидного равенства
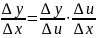 и переходя в нём к пределу при
и переходя в нём к пределу при
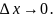 ч.т.д.
ч.т.д.
Производная обратной функций.
Пусть
 -
дифференцируемая и строго монотонная
функция на некотором промежутке X.
Если переменную
рассматривать как аргумент, а переменную
как ф-цию, то новая функция
-
дифференцируемая и строго монотонная
функция на некотором промежутке X.
Если переменную
рассматривать как аргумент, а переменную
как ф-цию, то новая функция
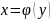
Является
обратной к данной и, как можно показать,
непрерывной на соответствующем промежутке
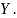
Теорема.
Для дифференцируемой ф-ции с производной
, не равной нулю, производная обратной
ы-ции равна обратной величине производной
данной ф-ции , т.е.
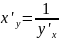 .
.
Док-ство:
По условию
,дифференцируема и
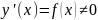 .
.
Пусть
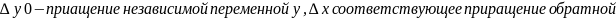
 .
.
Переходя к пределу в равенстве
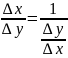 при
при
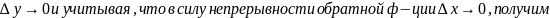
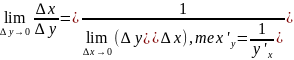 .
Ч.т.д.
.
Ч.т.д.
Монотонность функции. Критерии возрастания и убывания функции на интервале.
Возрастающие и убывающие функции объединяют общим понятием: монотонные функции.
Монотонная функция – это функция, меняющаяся в одном и том же направлении.
Функция возрастает, если большему значению аргумента соответствует большее значение функции. Говоря иначе, если при возрастании значения x значение y тоже возрастает, то это возрастающая функция.
Функция убывает, если большему значению аргумента соответствует меньшее значение функции. Говоря иначе, если при возрастании значения x значение y убывает, то это убывающая функция.
Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.
Функция постоянна (немонотонна), если она не убывает и не возрастает.
 Функция
f (x) называется возрастающей на
промежутке D, если для любых чисел x1 и
x2 из промежутка D таких, что x1 < x2,
выполняется неравенство f (x1) < f (x2).
Функция
f (x) называется возрастающей на
промежутке D, если для любых чисел x1 и
x2 из промежутка D таких, что x1 < x2,
выполняется неравенство f (x1) < f (x2).
Функция f (x) называется убывающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенство f (x1) > f (x2).
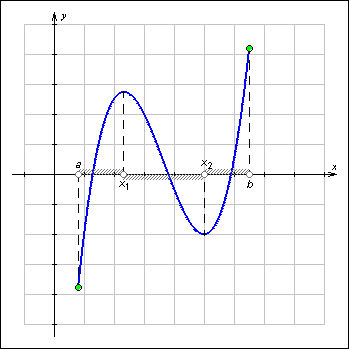
На показанном на рисунке графике функция y = f (x),………………….возрастает на каждом из промежутков [a; x1) и (x2; b] и убывает на промежутке (x1; x2). Обратите внимание, что функция возрастает на каждом из промежутков [a; x1) и (x2; b], но не на объединении промежутков
Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.
Заметим, что если f – монотонная функция на промежутке D (f (x)), то уравнение f (x) = const не может иметь более одного корня на этом промежутке.
Действительно, если x1 < x2 – корни этого уравнения на промежутке D (f(x)), то f (x1) = f (x2) = 0, что противоречит условию монотонности.
Перечислим свойства монотонных функций (предполагается, что все функции определены на некотором промежутке D).
Сумма нескольких возрастающих функций является возрастающей функцией.
Произведение неотрицательных возрастающих функций есть возрастающая функция.
Если функция f возрастает, то функции cf (c > 0) и f + c также возрастают, а функция cf (c < 0) убывает. Здесь c – некоторая константа.
Если функция f возрастает и сохраняет знак, то функция 1/f убывает.
Если функция f возрастает и неотрицательна, то ……… где…….. , также возрастает.
Если функция f возрастает и n – нечетное число, то f n также возрастает.
Композиция g (f (x)) возрастающих функций f и g также возрастает.
Аналогичные утверждения можно сформулировать и для убывающей функции.
Рисунок 1.3.5.1.Промежутки
возрастания и убывания функции