34. Основные правила дифференцирования.

Определение. Главная линейная относительно х часть малого приращения функцииназывается дифференциалом функции и обозначается dy.Если малое приращение функции можно представить в виде  , где   -б.м. функция более высокого порядка,чем х при   ( ), тогда .Основные правила дифференцирования:

1.      d(с)=0. 2.      d(u+w-v)= du+dw-dv.

3.      d(uv)=du·v+u·dv. 4.d(сu)=сd(u)

5.       .

6.      y=f(z),   ,   .

38.Дифференциал функции. Геометрический смысл дифференциала.

Определение. Главная линейная относительно х часть малого приращения функции называется дифференциалом функции и обозначается dy.

Если малое приращение функции можно представить в виде  , где   - б.м. функция более высокого порядка, чем х при   ( ), тогда .

Геометрический смысл дифференциала

Д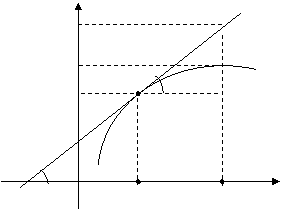 ана дифференцируемая функция y=f(x). Возьмем произвольную точку x₀ и проведем в этой точке касательную к графику. Дадим аргументу приращение 

Y                            B

         

     f(x₀+x)

 f(x₀)              A                    D

 

 

0       x₀            x₀+x        Х

Рассмотрим ABD:

,

,

,

.

Дифференциал функции в точке равен приращению ординаты касательной, проведенной к графику функции в данной точке.

40.Возрастание и убывание функций. Точки экстремума.

Определение. Числоваяфункция y=f(x) называется монотонно возрастающей (убывающей) на множестве А D(f), если большему значению аргумента соответствует большее (меньшее) значение функции:

x₁, x₂А D(f): x₁>x₂ f(x₁)>f(x₂)    ( f(x₁)<f(x₂) ).Из определения следует, что если функция возрастает (убывает), то

Приращение функции и приращение аргумента возрастающей (убывающей) функции имеют одинаковые (противоположные) знаки.

Теорема1. Если дифференцируемая функция возрастает (убывает) на некотором интервале, то в каждой точке этого интервала производная этой функции неотрицательна (неположительна).

Теорема2. Если производная функции на некотором интервале неотрицательна (неположительна), то на этом интервале функция возрастает (убывает).

41.Необходимое условие существования экстремума.

 Если дифференцируемая функция у=ƒ(х) имеет экстремум в точке х₀, то ее производная в этой точке равна нулю: ƒ'(х₀)=0.Пусть, для определенности, x₀ — точка максимума. Значит, в окрестности точки х₀ выполняется неравенство ƒ(х₀)>ƒ(х₀+∆х). Но тогда ,если ∆х>0, и ∆у/∆х>0, если ∆х<0.

П о условию теоремы производная существует. Переходя к пределу, при ∆х→0, получим ƒ'(x₀)≥0, если ∆х<0, и f'(х₀)≤0, если ∆х>0. Поэтому ƒ'(х₀)=0. Аналогично доказывается утверждение теоремы, если х₀ — точка минимума функции ƒ(х).

42.Критические точки. Достаточные условия существования экстремума.

 Непрерывная функция может иметь экстремум лишь в точках, где производная функции равна нулю или не существует. Такие точки называются кри тическими.

 Достаточные условия существования экстремума.Если непрерывная функция у=ƒ(х) дифференцируема в некоторой d -окрестности критической точки х₀ и при переходе через нее (слева направо) производная ƒ'(х) меняет знак с плюса на минус, то х₀ есть точка максимума; с минуса на плюс, то х₀ — точка минимума.