36.Дифференцирование логарифмических, показательных и степенных функций.

                             ,   ,                                         

37.Дифференцирование обратных функций и функций заданных параметрически.

Если дифференцируемая функция y=f(x),a<x<b имеет однозначную непрерывную обратную функцию x=g(x) и , то

39. Формула Тейлора.

Пусть функция ƒ(х) есть многочлен Р_n(х) степени n:ƒ(х)=Р_n(х)=а₀+а₁х+а₂х²+...+а_nхⁿ.Преобразуем этот многочлен также в многочлен степени n относительно разности х-х₀, где х₀ — произвольное число, т. е. представим Р_n(х) в видеР_n(х)=А₀+A₁(x-х₀)+А₂(х-х₀)²+...+А_n(х-х₀)ⁿ   (.1)Для нахождения коэффициентов А₀, А₁ ,..., А_n продифференцируем n раз равенство (1):

Р'_n(х)=А₁+2А₂(х-x₀)+3A₃(x-x₀)²+...+nA_n(x-x₀)^n-1,

Р_n''(х)=2А₂+2•3А₃(х-х₀)+...+n(n-1)А_n(х-х₀)^n-2,        

Р_n"'(х)=2•3А₃+2•3•4А₄(х-х₀)+...+n(n-1)(n-2)А_n(х-х₀)^n-3,

- - - - - - - - - - - - - - - - - -

Р_n⁽ⁿ⁾(х)=n(n-1)( n-2)...2•1А_n

Подставляя х=х₀ в полученные равенства и равенство (.1), имеем:

Подставляя найденные значения A₀,A₁,...,An в равенство (.1), получим разложение многочлена n-й степени Р_n(х) по степеням (х-х0):

54.  Формула Тейлора для функции нескольких переменных.

Пусть функция f(x)  задана в области R и имеет в R все частные производные до порядка m+1 включительно. Пусть   и    -- две точки области  , такие что весь отрезок между ними целиком лежит в R . Тогда для некоторой точки   этого отрезка имеет место равенство

  При m=1 получается линейное приближение функции f :

При m=2 получается квадратичное приближение функции f :

53. Касательная плоскость и нормаль к поверхности.

Нормалью к поверхности в некоторой ее точке называется прямая, направляющий вектор которой является нормальным к поверхности в этой точке и которая проходит через эту точку.Канонические уравнения нормали можно представить в виде

Касательной плоскостью к поверхности в некоторой точке называется плоскость, которая проходит через эту точку перпендикулярно нормали к поверхности в этой точке.уравнение касательной плоскости имеет вид:

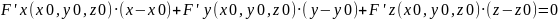
Если точка поверхности является особой, то в этой точке нормальный к поверхности вектор может не существовать, и, следовательно, поверхность может не иметь нормали и касательной плоскости.