11. Определение направляющего вектора. Общее и каноническое уравнения прямой на плоскости.

Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой.

Канонические уравнения прямой, проходящей через данные точки   и   имеют вид

.

Общее уравнение прямой имеет вид:  , где   – некоторые числа. При этом коэффициенты   одновременно не равны нулю, так как уравнение теряет смысл.

11. Общее и каноническое уравнения прямой и плоскости в пространстве.

  Канонические уравнения прямой

общее уравнение прямой

  	A1x + B1y + C1z + D1 = 0 A2x + B2y + C2z + D2 = 0

общее уравнение плоскости

Ax + By + Cz + D = 0

каноническое уравнение плоскости

Аx+By+Cz+D=0, где D = -Ax0-By0-Cz0.

11. Определение эллипса, гиперболы и параболы. Классификация кривых второго порядка.

Кривые второго порядка

Определение 11.1. Кривыми второго порядка на плоскости называются линии пересечения кругового конуса с плоскостями, не проходящими через его вершину.

Если такая плоскость пересекает все образующие одной полости конуса, то в сечении получается эллипс, при пересечении образующих обеих полостей - гипербола, а если секущая плоскость параллельна какой-либо образующей, то сечением конуса является парабола.

Замечание. Все кривые второго порядка задаются уравнениями второй степени от двух переменных.

Эллипс

Определение 11.2. Эллипсом называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F1 и F2 этой плоскости, называемых фокусами, есть величина постоянная.

Гипербола

Определение 11.5. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний до двух фиксированных точек F1 и F2 этой плоскости, называемых фокусами, есть величина постоянная.

Парабола

Определение 11.8. Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фокусом параболы, а прямая - ее директрисой.

11. Определения и примеры векторного пространства, векторов, линейной комбинации векторов.

Определения и примеры векторного пространства, векторов, линейной комбинации векторов.

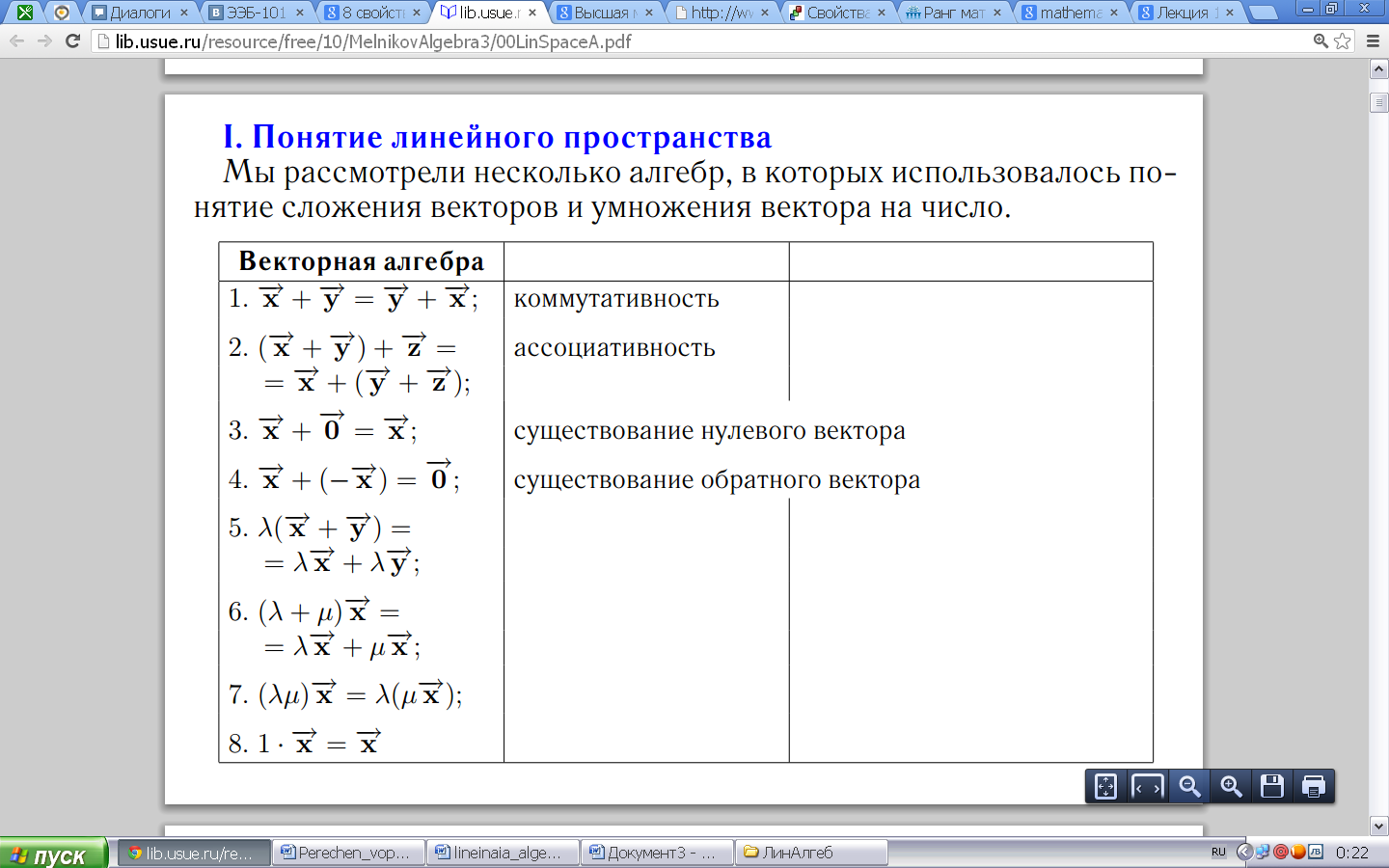
Непустое множ-во, в кот-ом опред-ны 2 операции: сложение и умножение на число, относит-но кот-х выпол-ны 8 аксиом назыв-ся линейн.вектор. прост-вом. пример: n-мерные векторы образ-т векторное простр-во, обозначаемое Rⁿ

Векторы а1, а2…а_m простр-ва Rⁿ наз-ся лин.независ-ми, если урав-е

Имеет единст.нулевое решение λ₁=0,… ,λ_k=0

Например, система двух векторов  1 = (1, 0) и  2 = (0, 2) является линейно независимой;

Векторы а1, а2…а_m простр-ва Rⁿ наз-ся лин.завис-ми, если найдутся числа λ_1,…, λ_k не равные нулю, для кот-ых выполнено равенство

свойства линейно зависимой системы векторов.

1. Система, состоящая из одного ненулевого вектора, линейно независима.

2. Система, содержащая нулевой вектор, всегда линейно зависима.

3. Система, содержащая более одного вектора, линейно зависима тогда и только тогда, когда среди ее векторов содержится по крайней мере один вектор, который линейно выражается через остальные.

Линейной комбинацией векторов (12.6) называется вектор вида

где λ1, λ2, ..., λk — любые действительные числа.

Например, пусть даны три вектора:  1 = (1, 2, 0),  2 = (2, 1, 1) и  3 = (-1, 1, -2). Их линейной комбинацией с коэффициентами соответственно 2, 3 и 4 является вектор   = (4, 11, -5).

В случае равенства (12.7) говорят также, что вектор   линейно выражается через векторы (12.6) или разлагается по этим векторам.