7. Повторные независимые испытания. Формула Бернулли. Теорема Пуассона.
Схема Бернулли. Если вероятность наступления события А в каждом испытании не меняется в зависимости от исходов других, то такие испытания называются независимыми относительно события А. Если независимые повторные испытания проводятся при одном и том же комплексе условий, то вероятность наступления события А в каждом испытании одна и та же.
Формула (теорема) Бернулли.
Если вероятность
Р наступления события А в каждом испытании
постоянна, то вероятность Рmn
того, что событие А наступит m
раз в n независимых
испытаниях, равна
=
где q=1-p
Число m0 наступления события А в n независимых испытаниях называется наивероятнейшим, если вероятность его осуществления Pm0,n по крайней мере не меньше вероятностей Pm,n других событий при любом m:
Решим первое неравенство системы, используя формулы Бернулли и числа сочетаний, запишем:
Преобразовав
которое, получим
и
Окончательно
получаем:
Теорема Пуассона.
Если вероятность р наступления события А в каждом испытании стремится к нулю при неограниченном увеличении числа n испытаний, причем произведение np стремится к постоянному числу λ, то вероятность Рmn того, что событие А появится m раз в n независимых испытаниях, удовлетворяет предельному равенству:
Формула Пуассона.
Если вероятность р постоянна и мала, число испытаний n велико и число λ=np <10, то из предельного равенства вытекает приближенная формула Пуассона:
8. Локальная и интегральная теоремы Муавра-Лапласа.
Локальная теорема Муавра – Лапласа.
Если вероятность
р наступления события А
в каждом испыта-нии постоянна и отлична
от 0 и 1, то вероятность Рmn
того, что событие А произойдет
m раз в n
независимых испытаниях при достаточно
большом числе n,
приближенно равна:
где - ф-ция Гаусса и
Приближенные значения вероятности Рmn, задаваемые ло-кальной формулой, на практике используются как точные при условии npq > 20.
1. Функция f(x) является четной, т.е. f(-x) = f(х).
2. Функция f(x) – монотонно убывающая при положительных значениях х, причем при х → ∞ f(x) → 0 (практически можно считать, что уже при х > 4 f(x) ≈ 0.
Интегральная теорема Муавра—Лапласа.
Используется при
решении интервальных задач, например
Если вероятность р наступления события А в каждом испыта-нии постоянна и отлична от 0 и 1, то вероятность того, что число m наступления события А в n независимых испытаниях заклю-чено в пределах от а до b (включительно), при достаточно боль-шом числе n приближенно равна:
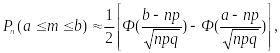
Где
-
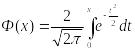ф-ция Лапласа( интеграл вероятостей)
При выполнении условия npq > 20 интегральная формула дает, как правило, удовлетворительную для практики погреш-ность вычисления вероятностей.
Значения функции Лапласа приведены в табл. II приложений.
1. Функция Ф(x) является нечетной, т.е. Ф(-x) = - Ф(х).
2. Функция Ф(x) – монотонно возрастающая, причем при х → ∞ Ф(x) → 1, практически можно считать, что уже при х > 4 Ф(x) ≈ 1.
Следствия.
Если вероятность р наступления события А в каждом испыта-нии постоянна и отлична от 0 и 1, то при достаточно большом числе n независимых испытаний вероятность того, что:
а) число m наступлений события А отличается от произведения nр не более, чем на величину ε > 0 (по абсолютной величине):
б) частость m /n события А заключена в пределах от α до β(включительно)
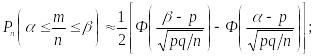
в) частость m /n события А отличается от его вероятности р не более, чем на величину Δ > 0 (по абсолютной величине):
