- •Определение слу. Метод Гаусса решения слу.
- •Определение матрицы, операций над матрицами. Свойства операций над матрицами.
- •3. Определение определителя. Основные свойства определителя (равноправие строк и столбцов, линейность, кососимметричность определителя).
- •Решение слу при помощи обратной матрицы. Теорема Крамера о решении слу.
- •Линейная модель межотраслевого баланса (модель Леонтьева).
- •Определения комплексного числа, операций над комплексными числами. Формула Муавра и формулы для нахождения корней из комплексного числа.
- •9. Определение свободного вектора и операций над ним.
- •Определение направляющего вектора. Общее и каноническое уравнения прямой на плоскости.
- •Общее и каноническое уравнения прямой и плоскости в пространстве.
- •Определение эллипса, гиперболы и параболы. Классификация кривых второго порядка.
- •Определения и примеры векторного пространства, векторов, линейной комбинации векторов.
- •Определение линейной зависимости и независимости системы векторов. Формулировка основных свойств линейно независимой системы векторов.
- •Собственные вектора и собственные значения
- •Теорема о связи характеристического многочлена и собственных значениях линейного оператора.
- •Линейная модель обмена.
- •Определение и примеры скалярного произведения векторов векторного пространства.
- •Свойства скалярного произведения.
- •Ортонормированная система векторов. Процесс ортогонализации.
- •Определения квадратичной формы, матрицы квадратичной формы, канонического вида квадратичной формы.
- •28. Метод Лагранжа приведения квадратичной формы к каноническому виду.
Определение слу. Метод Гаусса решения слу.
Определение. Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:
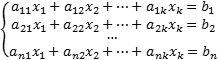
Смысл метода Гаусса заключается в том, чтобы преобразовать исходную систему уравнений и получить равносильную разрешенную или равносильную несовместную систему.
Итак, метод Гаусса состоит из следующих шагов:
Рассмотрим первое уравнение. Выберем первый ненулевой коэффициент и разделим все уравнение на него. Получим уравнение, в которое некоторая переменная xi входит с коэффициентом 1;
Вычтем это уравнение из всех остальных, умножая его на такие числа, чтобы коэффициенты при переменной xi в остальных уравнениях обнулились. Получим систему, разрешенную относительно переменной xi, и равносильную исходной;
Если возникают тривиальные уравнения (редко, но бывает; например, 0 = 0), вычеркиваем их из системы. В результате уравнений становится на одно меньше;
Повторяем предыдущие шаги не более n раз, где n — число уравнений в системе. Каждый раз выбираем для «обработки» новую переменную. Если возникают противоречивые уравнения (например, 0 = 8), система несовместна.
В результате через несколько шагов получим либо разрешенную систему (возможно, со свободными переменными), либо несовместную. Разрешенные системы распадаются на два случая:
Число переменных равно числу уравнений. Значит, система определена;
Число переменных больше числа уравнений. Собираем все свободные переменные справа — получаем формулы для разрешенных переменных. Эти формулы так и записываются в ответ.
Определение матрицы, операций над матрицами. Свойства операций над матрицами.
Матрицей размера m на n называется совокупность mn вещественных (комплексных) чисел или элементов другой структуры (многочлены, функции и т.д.), записанных в виде прямоугольной таблицы, которая состоит из m строк и n столбцов и взятая в круглые или прямоугольные или в двойные прямые скобки.
Операции над матрицами и иx свойства:
Сумма двух матриц A и B
A+B=B+A; (перестановочность или коммутативность операции сложения)
(A+B)+C = A+(B+C); (ассоциативность или сочетательное свойство)
A+O = O+A =A;
A+(-A)=(-A)+A=O.
Разность матриц A и B
Произведение матрицы A на число
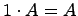
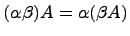
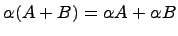 (Распределительное
свойство относительно сложения матриц);
(Распределительное
свойство относительно сложения матриц); (Распределительное
свойство относительно сложения чисел);
(Распределительное
свойство относительно сложения чисел);-A=(-1)A.
Произведение матриц A и B
(AB)C=A(BC); (Свойство ассоциативности)
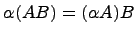 (Свойство
ассоциативности)
(Свойство
ассоциативности)A(B+C)=AB+AC, (A+B)C=AC+BC (Свойство дистрибутивности)
Транспонирование матриц A и B
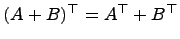
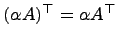 для
любого действительного числа
для
любого действительного числа
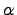 ;
;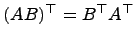
 для
любых матриц A и B, для которых имеют
смысл левые части равенств.
для
любых матриц A и B, для которых имеют
смысл левые части равенств.
3. Определение определителя. Основные свойства определителя (равноправие строк и столбцов, линейность, кососимметричность определителя).
Определитель – это некоторое число поставленное в соответствие квадратной матрице .
![]()
Для неквадратных матриц понятие определителя не вводится.
Свойства:
1)
Определитель — кососимметричная полилинейная
функция строк (столбцов) матрицы.
Полилинейность означает, что определитель
линеен по всем строкам (столбцам):![]() где
где ![]() и т. д. —
строчки матрицы,
и т. д. —
строчки матрицы, ![]() —
определитель такой матрицы.
—
определитель такой матрицы.
2) При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.
3) Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.
4) Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.
5) Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).
6) Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
7) Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.
8) Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.
9) Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
4. Определение алгебраического дополнения. Теорема о разложении определителя по строке. Теорема об определителе произведения двух матриц.
Алгебраическим
дополнением элемента ![]() матрицы
матрицы ![]() называется
число
называется
число
![]() ,
,
где ![]() — дополнительный
минор, определитель матрицы,
получающейся из исходной матрицы
путем
вычёркивания i -й
строки и j -го
столбца.
— дополнительный
минор, определитель матрицы,
получающейся из исходной матрицы
путем
вычёркивания i -й
строки и j -го
столбца.
Теорема Лапласа:
Пусть ![]() —
квадратная матрица размера
—
квадратная матрица размера ![]() .
Пусть также задан некоторый номер
строки
.
Пусть также задан некоторый номер
строки ![]() либо
номер столбца
либо
номер столбца ![]() матрицы
матрицы ![]() .
Тогда определитель
может
быть вычислен по следующим формулам:
.
Тогда определитель
может
быть вычислен по следующим формулам:
Разложение по -й строке:
Разложение по -му столбцу:
|
где ![]() —
алгебраическое дополнение к минору,
расположенному в строке с номером
и
столбце с номером
.
также
называют алгебраическим дополнением
к элементу
.
—
алгебраическое дополнение к минору,
расположенному в строке с номером
и
столбце с номером
.
также
называют алгебраическим дополнением
к элементу
.
Утверждение
является частным случаем теоремы
Лапласа. Достаточно в ней положить ![]() равным
1 и выбрать
-ую
строку, тогда минорами, расположенными
в этой строке будут сами элементы.
равным
1 и выбрать
-ую
строку, тогда минорами, расположенными
в этой строке будут сами элементы.
Теорема:
Определитель произведения двух квадратных матриц А и В одного и того же порядка равен произведению их определителей:
det(A*B)=detA*detB
5. Определение обратной матрицы. Свойства обратной матрицы. Критерий обратимости матриц.
Матрица
A
называется обратимой, если существует
такая матрица B,
что AB=BA=E.
Матрица B
называется обратной к A и обозначается
 .
.
Замечание
Если
матрица А обратима, то из равенства
 следует, что А квадратная матрица.
следует, что А квадратная матрица.
Свойства.
Пусть матрица А обратима, тогда
уществует единственная матрица обратная к А
 и
и
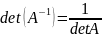
Если
 ,
то
,
то
 также обратима и
также обратима и
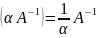
также обратима и
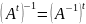
Пусть матрица B так же обратима. Тогда матрица ABобратима и

Критерий обратимости.
Матрица
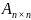 обратима
тогда и только тогда, когда
.
Более того справедлива формула
обратима
тогда и только тогда, когда
.
Более того справедлива формула