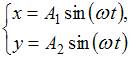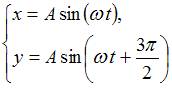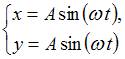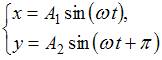- •Задание n 7 Тема: Сложение гармонических колебаний
- •Задание n 15 Тема: Работа. Энергия
- •Задание n 16 Тема: Элементы специальной теории относительности
- •Задание n 6 Тема: Уравнения Максвелла
- •Задание n 7 Тема: Законы постоянного тока
- •Задание n 10 Тема: Магнитостатика
- •Задание n 17 Тема: Законы сохранения в механике
- •Задание n 2 Тема: Второе начало термодинамики. Энтропия
- •Задание n 7 Тема: Законы постоянного тока
- •Задание n 8 Тема: Явление электромагнитной индукции
- •Задание n 1 Тема: Средняя энергия молекул
- •Задание n 2 Тема: Первое начало термодинамики. Работа при изопроцессах
- •Задание n 3 Тема: Второе начало термодинамики. Энтропия
- •Задание n 4 Тема: Распределения Максвелла и Больцмана
- •Задание n 8 Тема: Электрические и магнитные свойства вещества
- •Задание n 9 Тема: Уравнения Максвелла
- •Задание n 10 Тема: Явление электромагнитной индукции
- •Задание n 11 Тема: Элементы специальной теории относительности
- •Задание n 12 Тема: Динамика вращательного движения
- •Задание n 13 Тема: Законы сохранения в механике
- •Задание n 14 Тема: Кинематика поступательного и вращательного движения
- •Задание n 15 Тема: Работа. Энергия
- •Задание n 16 Тема: Динамика поступательного движения
- •Задание n 1 Тема: Свободные и вынужденные колебания
- •Задание n 2 Тема: Сложение гармонических колебаний
- •Задание n 3 Тема: Средняя энергия молекул
- •Задание n 13 Тема: Работа. Энергия
- •Задание n 17 Тема: Кинематика поступательного и вращательного движения
- •Задание n 18 Тема: Элементы специальной теории относительности
- •Задание n 1 Тема: Свободные и вынужденные колебания
- •Задание n 2 Тема: Сложение гармонических колебаний
- •Задание n 3 Тема: Распределения Максвелла и Больцмана
- •Задание n 8 Тема: Уравнения Максвелла
- •Задание n 9 Тема: Явление электромагнитной индукции
- •Задание n 10 Тема: Электрические и магнитные свойства вещества
- •Задание n 11 Тема: Законы постоянного тока
- •Задание n 14 Тема: Кинематика поступательного и вращательного движения
- •Задание n 18 Тема: Динамика вращательного движения
- •Варианты ответов:
- •II начало т-д. Циклы. Энтропия
- •120 См. Угловая скорость вращения шарика равна ...
ЗАДАНИЕ
N 1 сообщить
об ошибке
Тема:
Эффект Комптона. Световое
давление
Давление ![]() света
на поверхность, имеющую коэффициент
отражения
света
на поверхность, имеющую коэффициент
отражения ![]() ,
при энергетической
освещенности
,
при энергетической
освещенности 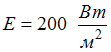 составляет ______ мкПа.
составляет ______ мкПа.
|
1
| |
Решение:
Давление
света определяется по формуле ![]() ,
где
,
где ![]() энергетическая
освещенность поверхности, то есть
энергия, падающая на единицу площади
поверхности в единицу времени;
энергетическая
освещенность поверхности, то есть
энергия, падающая на единицу площади
поверхности в единицу времени; ![]() скорость
света;
скорость
света; ![]() коэффициент
отражения. Давление света
коэффициент
отражения. Давление света 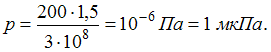

![]() ЗАДАНИЕ
N 2 сообщить
об ошибке
Тема:
Интерференция и дифракция света
На
узкую щель шириной
ЗАДАНИЕ
N 2 сообщить
об ошибке
Тема:
Интерференция и дифракция света
На
узкую щель шириной ![]() падает
нормально плоская световая волна с
длиной волны
падает
нормально плоская световая волна с
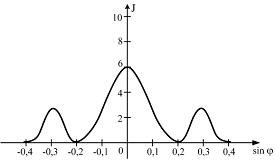
длиной волны ![]() На
рисунке схематически представлена
зависимость интенсивности света от
синуса угла дифракции:
На
рисунке схематически представлена
зависимость интенсивности света от
синуса угла дифракции:
 Если
расстояние от щели до экрана составляет
Если
расстояние от щели до экрана составляет ![]() ,
то ширина центрального максимума (в
,
то ширина центрального максимума (в ![]() )
равна …
(Учесть, что
)
равна …
(Учесть, что ![]() .)
.)
|
20
| |
Решение:
Ширина
центрального максимума равна расстоянию
между минимумами первого порядка.
Условие минимумов для дифракции на щели
имеет вид ![]() ,
где
–
ширина щели,
,
где
–
ширина щели, ![]() –
угол дифракции,
–
угол дифракции, ![]() –
порядок минимума,
–
порядок минимума, ![]() –
длина световой волны. Из рисунка для
минимума первого порядка
–
длина световой волны. Из рисунка для
минимума первого порядка ![]() .
Тогда с учетом того, что
,
получаем
.
Тогда с учетом того, что
,
получаем ![]() .
.
ЗАДАНИЕ
N 3 сообщить
об ошибке
Тема:
Тепловое излучение. Фотоэффект
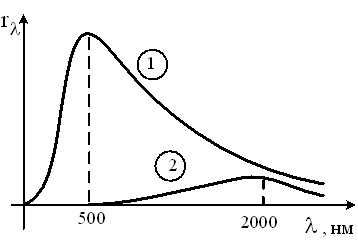
На
рисунке представлены кривые зависимости
спектральной плотности энергетической
светимости абсолютно черного тела от
длины волны при разных температурах.
Отношение энергетических светимостей ![]() при
этих температурах равно …
при
этих температурах равно …
|
|
|
256 |
|
|
|
16 |
|
|
|
|
|
|
|
|
Решение:
Распределение
энергии в спектре излучения абсолютно
черного тела в зависимости от частоты
излучения и температуры объясняется
законами Стефана – Больцмана и Вина.
Энергетическая светимость ![]() абсолютно
черного тела связана со спектральной
плотностью энергетической светимости
соотношением
абсолютно
черного тела связана со спектральной
плотностью энергетической светимости
соотношением 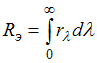 .
В соответствии с законом Стефана
− Больцмана
.
В соответствии с законом Стефана
− Больцмана ![]() ,
где
,
где ![]() постоянная
Стефана – Больцмана. Согласно закону
смещения Вина,
постоянная
Стефана – Больцмана. Согласно закону
смещения Вина, ![]() ,
где
,
где ![]() длина
волны, на которую приходится максимум
спектральной плотности энергетической
светимости;
длина
волны, на которую приходится максимум
спектральной плотности энергетической
светимости; ![]() постоянная
Вина. Отсюда
постоянная
Вина. Отсюда 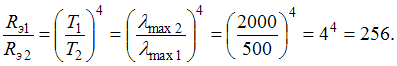
ЗАДАНИЕ
N 4 сообщить
об ошибке
Тема:
Поляризация и дисперсия света
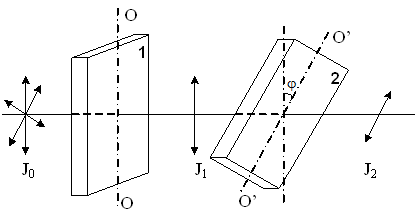
На
пути естественного света помещены две
пластинки турмалина. После прохождения
пластинки 1 свет
полностью поляризован. Если J1 и J2 –
интенсивности света, прошедшего пластинки
соответственно 1 и 2,
и ![]() ,
тогда угол между направлениями OO и O’O’
равен …
,
тогда угол между направлениями OO и O’O’
равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Интенсивность ![]() света,
прошедшего через вторую пластинку
турмалина (анализатор), меняется в
зависимости от угла
между
направлениями OO и O’O’ оптических осей
пластин турмалина по закону Малюса:
света,
прошедшего через вторую пластинку
турмалина (анализатор), меняется в
зависимости от угла
между
направлениями OO и O’O’ оптических осей
пластин турмалина по закону Малюса: ![]() ,
где
,
где ![]() –
интенсивность плоскополяризованного
света, прошедшего через первую
пластинку1 (поляризатор).
Отсюда
–
интенсивность плоскополяризованного
света, прошедшего через первую
пластинку1 (поляризатор).
Отсюда 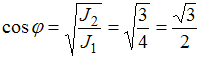 ,
а угол
,
а угол ![]() .
.
ЗАДАНИЕ N 5 сообщить об ошибке Тема: Второе начало термодинамики. Энтропия В ходе необратимого процесса при поступлении в неизолированную термодинамическую систему тепла для приращения энтропии верным будет соотношение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ
N 6 сообщить
об ошибке
Тема:
Средняя энергия молекул
Средняя
кинетическая энергия молекул газа при
температуре ![]() зависит
от их конфигурации и структуры, что
связано с возможностью различных видов
движения атомов в молекуле и самой
молекулы. При условии, что имеет место
поступательное, вращательное движение
молекулы как целого и колебательное
движение атомов в молекуле, средняя
кинетическая энергия молекулы кислорода
(
зависит
от их конфигурации и структуры, что
связано с возможностью различных видов
движения атомов в молекуле и самой
молекулы. При условии, что имеет место
поступательное, вращательное движение
молекулы как целого и колебательное
движение атомов в молекуле, средняя
кинетическая энергия молекулы кислорода
(![]() )
равна …
)
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Для
статистической системы в состоянии
термодинамического равновесия на каждую
поступательную и вращательную степени
свободы приходится в среднем кинетическая
энергия, равная ![]() ,
а на каждую колебательную степень
–
,
а на каждую колебательную степень
– ![]() Средняя
кинетическая энергия молекулы равна:
Средняя
кинетическая энергия молекулы равна: ![]() .
Здесь
.
Здесь ![]() –
сумма числа поступательных, числа
вращательных и удвоенного числа
колебательных степеней свободы
молекулы:
–
сумма числа поступательных, числа
вращательных и удвоенного числа
колебательных степеней свободы
молекулы: ![]() ,
где
,
где ![]() –
число степеней свободы поступательного
движения, равное 3;
–
число степеней свободы поступательного
движения, равное 3; ![]() –
число степеней свободы вращательного
движения, которое может быть равно 0, 2,
3;
–
число степеней свободы вращательного
движения, которое может быть равно 0, 2,
3; ![]() –
число степеней свободы колебательного
движения, минимальное количество которых
равно 1.
Для молекулярного кислорода
(двухатомной молекулы)
–
число степеней свободы колебательного
движения, минимальное количество которых
равно 1.
Для молекулярного кислорода
(двухатомной молекулы) ![]() ,
, ![]() и
и ![]() .
Следовательно,
.
Следовательно, ![]() .
Тогда средняя энергия молекулы
кислорода(
) равна:
.
Тогда средняя энергия молекулы
кислорода(
) равна: ![]() .
.
ЗАДАНИЕ
N 7 сообщить
об ошибке
Тема:
Распределения Максвелла и Больцмана
На
рисунке представлен график функции
распределения молекул идеального газа
по скоростям (распределение Максвелла),
где ![]() –
доля молекул, скорости которых заключены
в интервале скоростей от
–
доля молекул, скорости которых заключены
в интервале скоростей от ![]() до
до ![]() в
расчете на единицу этого интервала.
в
расчете на единицу этого интервала.
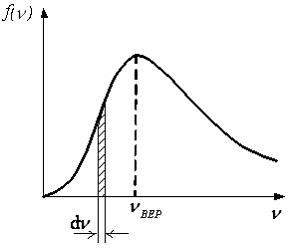 Для
этой функции неверными являются
утверждения, что …
Для
этой функции неверными являются
утверждения, что …
|
|
|
при понижении температуры величина максимума функции уменьшается |
|
|
|
при понижении температуры площадь под кривой уменьшается |
|
|
|
с ростом температуры наиболее вероятная скорость молекул увеличивается |
|
|
|
положение максимума кривой зависит не только от температуры, но и от природы газа |

ЗАДАНИЕ
N 8 сообщить
об ошибке
Тема:
Первое начало термодинамики. Работа
при изопроцессах
При
изотермическом расширении 0,5 моля газа
при температуре 200 К объем
увеличился в ![]() раз
(
раз
(![]() ).
Работа газа (в Дж)
равна …
).
Работа газа (в Дж)
равна …
|
831
| |
Решение:
При
изотермическом расширении газа работа
находится по формуле: 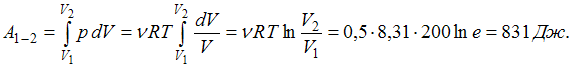
ЗАДАНИЕ
N 9 сообщить
об ошибке
Тема:
Волны. Уравнение волны
На
рисунке представлена мгновенная
фотография электрической составляющей
электромагнитной волны, переходящей
из среды 1 в
среду 2 перпендикулярно
границе раздела АВ.
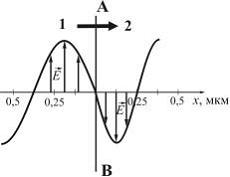 Относительный
показатель преломления
Относительный
показатель преломления ![]() двух
сред равен …
двух
сред равен …
|
|
|
1,50 |
|
|
|
1,33 |
|
|
|
0,67 |
|
|
|
0,84 |
Решение:
Относительный
показатель преломления двух сред равен
отношению их абсолютных показателей
преломления: ![]() ,
где
,
где ![]() и
и ![]() –
абсолютные показатели преломления
среды 1 и среды
–
абсолютные показатели преломления
среды 1 и среды ![]() ,
равные отношению скорости
,
равные отношению скорости ![]() электромагнитной
волны в вакууме к фазовым скоростям
электромагнитной
волны в вакууме к фазовым скоростям ![]() и
и ![]() в
этих средах. Следовательно,
в
этих средах. Следовательно, ![]() .
Скорость волны
.
Скорость волны ![]() ,
где
–
частота;
,
где
–
частота; ![]() длина
волны, которую можно определить, используя
рисунок. Тогда при условии
длина
волны, которую можно определить, используя
рисунок. Тогда при условии![]() (при
переходе электромагнитной волны из
среды 1 в среду 2 частота не меняется)
относительный показатель преломления
равен:
(при
переходе электромагнитной волны из
среды 1 в среду 2 частота не меняется)
относительный показатель преломления
равен: 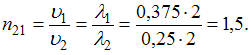
ЗАДАНИЕ
N 10 сообщить
об ошибке
Тема:
Сложение гармонических колебаний
Сопротивление,
катушка индуктивности и конденсатор
соединены последовательно и включены
в цепь переменного тока, изменяющегося
по закону![]() (А).
На рисунке схематически представлена
фазовая диаграмма падений напряжения
на указанных элементах. Амплитудные
значения напряжений соответственно
равны: на сопротивлении
(А).
На рисунке схематически представлена
фазовая диаграмма падений напряжения
на указанных элементах. Амплитудные
значения напряжений соответственно
равны: на сопротивлении ![]() ;
на катушке индуктивности
;
на катушке индуктивности ![]() ;
на конденсаторе
;
на конденсаторе ![]()
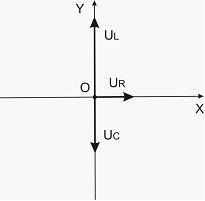 Установите
соответствие между сопротивлением и
его численным значением.
1. Полное
сопротивление
2. Активное
сопротивление
3. Реактивное
сопротивление
Установите
соответствие между сопротивлением и
его численным значением.
1. Полное
сопротивление
2. Активное
сопротивление
3. Реактивное
сопротивление
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
Решение:
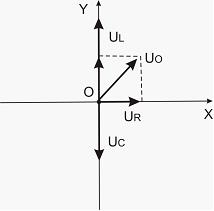 Для
решения используется метод векторных
диаграмм. Длина вектора равна амплитудному
значению напряжения, а угол, который
вектор составляет с осью ОХ, равен
разности фаз колебаний напряжения на
соответствующем элементе и силы тока
в цепи. Амплитудное значение полного
напряжения равно
Для
решения используется метод векторных
диаграмм. Длина вектора равна амплитудному
значению напряжения, а угол, который
вектор составляет с осью ОХ, равен
разности фаз колебаний напряжения на
соответствующем элементе и силы тока
в цепи. Амплитудное значение полного
напряжения равно ![]() .
Величина
.
Величина ![]() Полное
сопротивление цепи связано с амплитудными
значениями тока и напряжения законом
Ома:
Полное
сопротивление цепи связано с амплитудными
значениями тока и напряжения законом
Ома:  .
Амплитудное значение силы тока, как это
следует из закона его изменения, равно
.
Амплитудное значение силы тока, как это
следует из закона его изменения, равно ![]() .
Тогда
.
Тогда  Активное
сопротивление
Активное
сопротивление 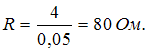 Полное
сопротивление цепи равно:
Полное
сопротивление цепи равно: ![]() ,
где
,
где ![]() реактивное
сопротивление;
реактивное
сопротивление; ![]() индуктивное
и емкостное сопротивления соответственно.
Отсюда
индуктивное
и емкостное сопротивления соответственно.
Отсюда ![]()
ЗАДАНИЕ N 11 сообщить об ошибке Тема: Свободные и вынужденные колебания В колебательном контуре за один период колебаний в тепло переходит 4,0 % энергии. Добротность контура равна …
|
157
| |
Решение:
По
определению добротность равна 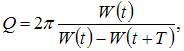 где
где ![]() и
и ![]() –
энергия контура в некоторый момент
времени и спустя период соответственно.
Следовательно,
–
энергия контура в некоторый момент
времени и спустя период соответственно.
Следовательно, 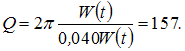
ЗАДАНИЕ
N 12 сообщить
об ошибке
Тема:
Энергия волны. Перенос энергии
волной
Плоская
электромагнитная волна распространяется
в диэлектрике с проницаемостью ![]() .
Если амплитудное значение электрического
вектора волны
.
Если амплитудное значение электрического
вектора волны ![]() ,
то интенсивность волны равна …
(Электрическая
постоянная равна
,
то интенсивность волны равна …
(Электрическая
постоянная равна ![]() .
Полученный
ответ умножьте на
.
Полученный
ответ умножьте на ![]() и
округлите до целого числа.)
и
округлите до целого числа.)
|
8
| |
Решение:
Интенсивностью
волны называется скалярная величина,
равная модулю среднего значения вектора
плотности потока энергии (вектора Умова
– Пойнтинга) ![]() ,
где
,
где ![]() –
скорость волны,
–
скорость волны, ![]() –
объемная плотность ее энергии. Среднее
значение объемной плотности энергии
электромагнитной волны определяется
выражением
–
объемная плотность ее энергии. Среднее
значение объемной плотности энергии
электромагнитной волны определяется
выражением ![]() ,
а скорость волны в среде
,
а скорость волны в среде ![]() ,
где
,
где ![]() –
абсолютный показатель преломления
среды, причем
–
абсолютный показатель преломления
среды, причем ![]() .
Для неферромагнитных сред
.
Для неферромагнитных сред ![]() .
Таким образом, выражение для интенсивности
электромагнитной волны можно представить
в виде
.
Таким образом, выражение для интенсивности
электромагнитной волны можно представить
в виде 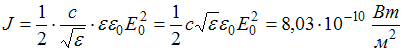 .
.
ЗАДАНИЕ
N 13 сообщить
об ошибке
Тема:
Спектр атома водорода. Правило отбора
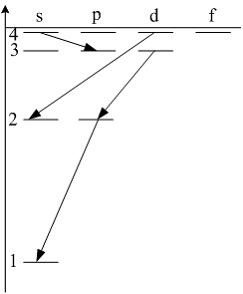
Закон
сохранения момента импульса накладывает
ограничения на возможные переходы
электрона в атоме с одного уровня на
другой (правило отбора). В энергетическом
спектре атома водорода (см. рис.)
запрещенным является переход …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 14 сообщить об ошибке Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга В опыте Дэвиссона и Джермера исследовалась дифракция прошедших ускоряющее напряжение электронов на монокристалле никеля. Если ускоряющее напряжение увеличить в 8 раз, то длина волны де Бройля электрона _____ раз(-а).
|
|
|
уменьшится
в |
|
|
|
увеличится в 8 |
|
|
|
уменьшится в 4 |
|
|
|
увеличится
в |
ЗАДАНИЕ
N 15 сообщить
об ошибке
Тема:
Уравнение Шредингера (конкретные
ситуации)
Момент
импульса электрона в атоме и его
пространственные ориентации могут быть
условно изображены векторной схемой,
на которой длина вектора пропорциональна
модулю орбитального момента
импульса ![]() электрона. На
рисунке приведены возможные ориентации
вектора
.
электрона. На
рисунке приведены возможные ориентации
вектора
.
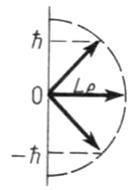 Значение
орбитального квантового числа и
минимальное значение главного квантового
числа для указанного состояния
соответственно равны …
Значение
орбитального квантового числа и
минимальное значение главного квантового
числа для указанного состояния
соответственно равны …
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
, |
ЗАДАНИЕ
N 16 сообщить
об ошибке
Тема:
Уравнения Шредингера (общие свойства)
Верным
для уравнения Шредингера 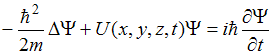 является
утверждение, что оно …
является
утверждение, что оно …
|
|
|
является нестационарным |
|
|
|
соответствует одномерному случаю |
|
|
|
является стационарным |
|
|
|
описывает состояние микрочастицы в одномерном бесконечно глубоком прямоугольном потенциальном ящике |
Решение:
Уравнение
называют
нестационарным (временным) уравнением
Шредингера, так как функция ![]() является
функцией не только пространственных
координат, но и времени, и оно содержит
производную от функции
является
функцией не только пространственных
координат, но и времени, и оно содержит
производную от функции ![]() по
времени.
по
времени.
ЗАДАНИЕ
N 17 сообщить
об ошибке
Тема:
Электростатическое поле в
вакууме
Электростатическое
поле создано бесконечной равномерно
заряженной плоскостью (![]() – поверхностная
плотность зарядов).
– поверхностная
плотность зарядов).
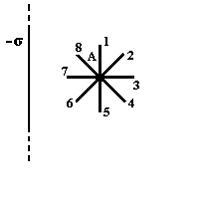 Градиент
потенциала поля в точке А ориентирован
в направлении …
Градиент
потенциала поля в точке А ориентирован
в направлении …
|
3 |
ЗАДАНИЕ
N 18 сообщить
об ошибке
Тема:
Явление электромагнитной индукции
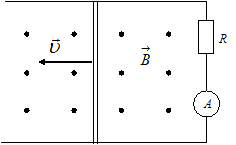
По
параллельным металлическим проводникам,
расположенным в однородном магнитном
поле, с постоянной скоростью перемещается
проводящая перемычка, длиной ![]() (см.
рис.). Если сопротивлением перемычки и
направляющих можно пренебречь, то
зависимость индукционного тока от
времени можно представить графиком …
(см.
рис.). Если сопротивлением перемычки и
направляющих можно пренебречь, то
зависимость индукционного тока от
времени можно представить графиком …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 19 сообщить об ошибке Тема: Электрические и магнитные свойства вещества Диамагнетиком является вещество с магнитной проницаемостью …
|
|
|
|
|
|
|
=1,00036 |
|
|
|
=2600 |
|
|
|
=1 |
ЗАДАНИЕ
N 20 сообщить
об ошибке
Тема:
Магнитостатика
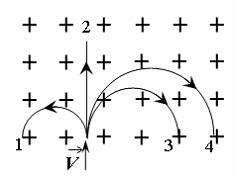
На
рисунке показаны траектории заряженных
частиц, с одинаковой скоростью влетающих
в однородное магнитное поле, перпендикулярное
плоскости рисунка. При этом для зарядов
и удельных зарядов частиц верным является
утверждение …
|
|
|
|
|
|
|
,
, |
|
|
|
|
|
|
|
|
Решение:
На
заряженную частицу, движущуюся в
магнитном поле, действует сила Лоренца.
В том случае, когда скорость
частицы ![]() перпендикулярна
линиям магнитной индукции, направление
силы Лоренца удобно находить по правилу
левой руки. Тогда из рисунка следует,
что
,
,
,
.
В данном случае траектории заряженных
частиц – дуги окружностей с различающимися
радиусами. Поскольку радиус окружности
обратно пропорционален удельному заряду
частицы,
перпендикулярна
линиям магнитной индукции, направление
силы Лоренца удобно находить по правилу
левой руки. Тогда из рисунка следует,
что
,
,
,
.
В данном случае траектории заряженных
частиц – дуги окружностей с различающимися
радиусами. Поскольку радиус окружности
обратно пропорционален удельному заряду
частицы, 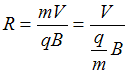 ,
то из рисунка следует, что
.
,
то из рисунка следует, что
.
ЗАДАНИЕ
N 21 сообщить
об ошибке
Тема:
Законы постоянного тока
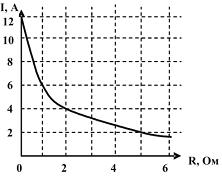
На
рисунке представлены результаты
экспериментального исследования
зависимости силы тока в цепи от значения
сопротивления, подключенного к источнику
постоянного тока. ЭДС источника и его
внутреннее сопротивление соответственно
равны …
|
|
|
12 В, 1 Ом |
|
|
|
9 В, 0,5 Ом |
|
|
|
24 В, 3 Ом |
|
|
|
18 В, 2 Ом |
ЗАДАНИЕ
N 22 сообщить
об ошибке
Тема:
Уравнения Максвелла
Полная
система уравнений Максвелла для
электромагнитного поля в интегральной
форме имеет вид:
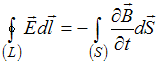 ,
,
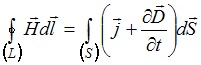 ,
,
 ,
,
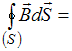 0.
Система
распадается на две группы независимых
уравнений:
0.
Система
распадается на две группы независимых
уравнений:
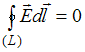 ,
,
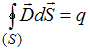 ;
;
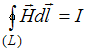 ,
0 –
при
условии, что …
,
0 –
при
условии, что …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
Решение:
Из
сопоставления второй системы с первой
следует, что  и
и 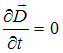 ,
то есть магнитное и электрическое поля
стационарны:
и
(а
следовательно, и
,
то есть магнитное и электрическое поля
стационарны:
и
(а
следовательно, и ![]() ).
В этом случае электрическое и магнитное
поля независимы друг от друга.
).
В этом случае электрическое и магнитное
поля независимы друг от друга.
ЗАДАНИЕ
N 23 сообщить
об ошибке
Тема:
Работа. Энергия
Для
того чтобы раскрутить стержень массы ![]() и
длины
и
длины ![]() (см.
рисунок) вокруг вертикальной оси,
проходящей перпендикулярно стержню
через его середину, до угловой скорости
(см.
рисунок) вокруг вертикальной оси,
проходящей перпендикулярно стержню
через его середину, до угловой скорости ![]() ,
необходимо совершить работу
,
необходимо совершить работу ![]() .
.
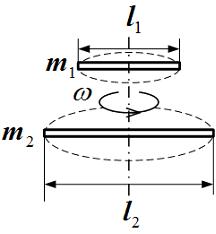 Для
того чтобы раскрутить до той же угловой
скорости стержень массы
Для
того чтобы раскрутить до той же угловой
скорости стержень массы ![]() и
длины
и
длины ![]() ,
необходимо совершить работу в _____
раз(-а) бόльшую,
чем
.
,
необходимо совершить работу в _____
раз(-а) бόльшую,
чем
.
|
8
| |
Решение:
Совершенная
работа равна кинетической энергии
вращательного движения стержня  ,
где момент инерции стержня
,
где момент инерции стержня ![]() пропорционален
массе и квадрату длины,
пропорционален
массе и квадрату длины, ![]() (момент
инерции стержня массы
(момент
инерции стержня массы ![]() и
длины
относительно
оси, проходящей перпендикулярно ему
через середину стержня, равен
и
длины
относительно
оси, проходящей перпендикулярно ему
через середину стержня, равен ![]() ).
Следовательно, работа по раскручиванию
до такой же угловой скорости
стержня
вдвое бόльшей
массы и в два раза длиннее будет в 8 раз
больше:
).
Следовательно, работа по раскручиванию
до такой же угловой скорости
стержня
вдвое бόльшей
массы и в два раза длиннее будет в 8 раз
больше: ![]() .
.
ЗАДАНИЕ
N 24 сообщить
об ошибке
Тема:
Динамика поступательного движения
Тело
массой ![]() движется
равномерно по вогнутому мосту со
скоростью
движется
равномерно по вогнутому мосту со
скоростью ![]() .
В нижней точке сила давления тела
на мост вдвое превосходит силу тяжести.
Радиус кривизны моста (в
.
В нижней точке сила давления тела
на мост вдвое превосходит силу тяжести.
Радиус кривизны моста (в ![]() )
равен …
)
равен …
|
10 |
ЗАДАНИЕ
N 25 сообщить
об ошибке
Тема:
Элементы специальной теории
относительности
Космический
корабль летит со скоростью ![]() (
скорость
света в вакууме) в системе отсчета,
связанной с некоторой планетой. Один
из космонавтов медленно поворачивает
метровый стержень из положения 1,
перпендикулярного направлению движения
корабля, в положение 2, параллельное
направлению движения. Длина этого
стержня с точки зрения другого космонавта
…
(
скорость
света в вакууме) в системе отсчета,
связанной с некоторой планетой. Один
из космонавтов медленно поворачивает
метровый стержень из положения 1,
перпендикулярного направлению движения
корабля, в положение 2, параллельное
направлению движения. Длина этого
стержня с точки зрения другого космонавта
…
|
|
|
равна 1,0 м при любой его ориентации |
|
|
|
изменяется от 1,0 м в положении 1 до 1,67 м в положении 2 |
|
|
|
изменяется от 1,0 м в положении 1 до 0,6 м в положении 2 |
|
|
|
изменяется от 0,6 м в положении 1 до 1,0 м в положении 2 |
Решение:
Движение
макроскопических тел со скоростями,
соизмеримыми со скоростью света в
вакууме, изучается релятивистской
механикой. Одним из следствий преобразований
Лоренца является так называемое Лоренцево
сокращение длины, состоящее в том, что
линейные размеры тела сокращаются в
направлении движения: 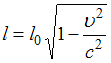 .
Здесь
.
Здесь ![]() –
длина тела в системе отсчета, относительно
которой тело неподвижно;
–
длина тела в системе отсчета, относительно
которой тело движется со скоростью
.
При этом поперечные размеры тела не
изменяются. Поскольку с точки зрения
другого космонавта стержень покоится
и в положении 1, и в положении 2, то длина
стержня равна 1,0 м при
любой его ориентации.
–
длина тела в системе отсчета, относительно
которой тело неподвижно;
–
длина тела в системе отсчета, относительно
которой тело движется со скоростью
.
При этом поперечные размеры тела не
изменяются. Поскольку с точки зрения
другого космонавта стержень покоится
и в положении 1, и в положении 2, то длина
стержня равна 1,0 м при
любой его ориентации.
ЗАДАНИЕ
N 26 сообщить
об ошибке
Тема:
Динамика вращательного движения
Величина
момента импульса тела изменяется с
течением времени по закону ![]() (в
единицах СИ). Если в момент времени
(в
единицах СИ). Если в момент времени ![]() угловое
ускорение составляет
угловое
ускорение составляет ![]() ,
то момент инерции тела (в
,
то момент инерции тела (в ![]() )
равен …
)
равен …
|
|
|
5 |
|
|
|
6 |
|
|
|
0,2 |
|
|
|
0,5 |
Решение:
Cкорость
изменения величины момента импульса
относительно неподвижной оси равна
величине суммарного момента внешних
сил относительно этой оси, то есть
![]() где
где ![]() –
величина момента импульса,
–
величина момента импульса, ![]() –
величина момента силы. Вычислив
производную от функции, характеризующей
зависимость величины момента импульса
от времени, получим величину момента
силы
–
величина момента силы. Вычислив
производную от функции, характеризующей
зависимость величины момента импульса
от времени, получим величину момента
силы ![]() . Используя
основной закон динамики вращательного
движения твердого тела вокруг неподвижной
оси, можем определить его момент инерции:
. Используя
основной закон динамики вращательного
движения твердого тела вокруг неподвижной
оси, можем определить его момент инерции:
![]() .
.
ЗАДАНИЕ
N 27 сообщить
об ошибке
Тема:
Кинематика поступательного и вращательного
движения
Тело
движется с постоянной по величине
скоростью по траектории, изображенной
на рисунке:
 Для
величин полного ускорения а тела
в точках А и В справедливо соотношение …
Для
величин полного ускорения а тела
в точках А и В справедливо соотношение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
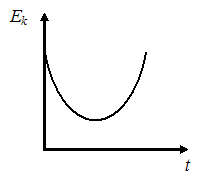
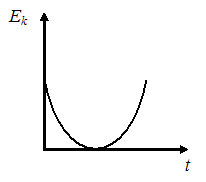
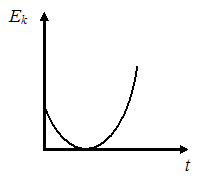
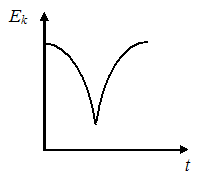
ЗАДАНИЕ N 28 сообщить об ошибке Тема: Законы сохранения в механике График зависимости кинетической энергии от времени для тела, брошенного с поверхности земли под некоторым углом к горизонту, имеет вид, показанный на рисунке …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Кинетическая
энергия тела 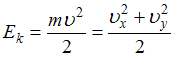 ,
где
,
где ![]() и
и ![]() –
проекции скорости тела на оси OX и OY
соответственно. Для тела, брошенного
под углом α к
горизонту,
–
проекции скорости тела на оси OX и OY
соответственно. Для тела, брошенного
под углом α к
горизонту, ![]() ,
, ![]() .
Тогда
.
Тогда 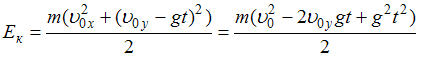 .
Это уравнение параболы со смещенной
вершиной, ветви которой направлены
вверх, причем
.
Это уравнение параболы со смещенной
вершиной, ветви которой направлены
вверх, причем ![]() .
Поэтому график зависимости кинетической
энергии тела, брошенного с поверхности
земли под некоторым углом к горизонту,
от времени имеет вид:
.
Поэтому график зависимости кинетической
энергии тела, брошенного с поверхности
земли под некоторым углом к горизонту,
от времени имеет вид:
Физика i-exam вариант 1
ЗАДАНИЕ N 1 Тема: Электростатическое поле в вакууме
Электростатическое
поле создано положительно заряженной
сферой.
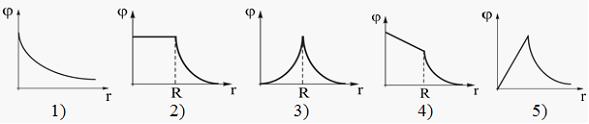 Правильно
отражает зависимость потенциала от
расстояния рисунок …
Правильно
отражает зависимость потенциала от
расстояния рисунок …
|
2 |
ЗАДАНИЕ N 2 Тема: Законы постоянного тока
На рисунке
представлена зависимость плотности
тока j,
протекающего в проводниках 1 и 2, от
напряженности электрического
поля Е:
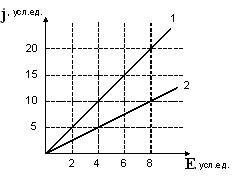 Отношение
удельных сопротивлений r1/r2 этих
проводников равно …
Отношение
удельных сопротивлений r1/r2 этих
проводников равно …
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
4 |
ЗАДАНИЕ N 3 Тема: Магнитостатика
Два
заряда ![]() и
и ![]() движутся
параллельно в одну сторону на
расстоянии r друг
от друга, как показано на рисунке:
движутся
параллельно в одну сторону на
расстоянии r друг
от друга, как показано на рисунке:
 Магнитная
составляющая силы, действующей на второй
заряд со стороны первого заряда, имеет
направление …
Магнитная
составляющая силы, действующей на второй
заряд со стороны первого заряда, имеет
направление …
|
|
|
4 |
|
|
|
2 |
|
|
|
3 |
|
|
|
1 |
Решение:
Индукция
магнитного поля свободно движущегося
заряда равна 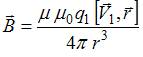 ,
где
,
где ![]() заряд
частицы,
заряд
частицы, ![]() скорость
частицы,
скорость
частицы, ![]() радиус-вектор,
характеризующий положение
заряда
радиус-вектор,
характеризующий положение
заряда ![]() относительно
заряда
относительно
заряда ![]() .
Используя определение векторного
произведения, находим, что вектор
.
Используя определение векторного
произведения, находим, что вектор ![]() в
месте нахождения заряда
направлен
«от нас». Сила Лоренца
в
месте нахождения заряда
направлен
«от нас». Сила Лоренца ![]() по
правилу левой руки имеет направление
4.
по
правилу левой руки имеет направление
4.

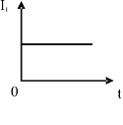
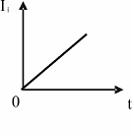
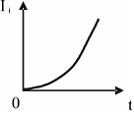
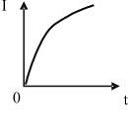
ЗАДАНИЕ N 4 Тема: Явление электромагнитной индукции
На рисунке
показана зависимость силы тока от
времени в электрической цепи с
индуктивностью 1 мГн:
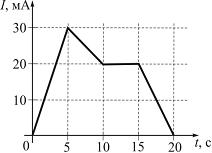 Модуль
среднего значения ЭДС самоиндукции в
интервале от 0 до 5 с (в мкВ)
равен …
Модуль
среднего значения ЭДС самоиндукции в
интервале от 0 до 5 с (в мкВ)
равен …
|
|
|
6 |
|
|
|
30 |
|
|
|
0 |
|
|
|
15 |
ЗАДАНИЕ N 5 Тема: Уравнения Максвелла
Утверждение «Переменное электрическое поле, наряду с электрическим током, является источником магнитного поля» раскрывает физический смысл уравнения …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 6 Тема: Электрические и магнитные свойства вещества
На рисунке
представлены графики, отражающие
характер зависимости величины
намагниченности I вещества
(по модулю) от напряженности магнитного
поля Н:
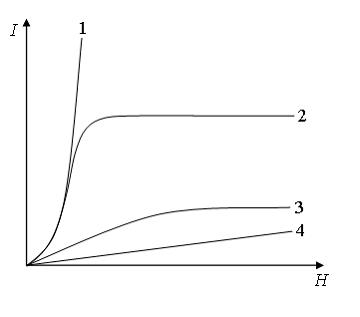 Парамагнетикам
соответствует кривая …
Парамагнетикам
соответствует кривая …
|
|
|
3 |
|
|
|
1 |
|
|
|
2 |
|
|
|
4 |
Решение:
К
парамагнетикам относятся вещества,
атомы (молекулы) которых обладают
собственным магнитным моментом. Однако
вследствие теплового движения молекул
их магнитные моменты ориентированы
беспорядочно в отсутствие внешнего
магнитного поля, и намагниченность
вещества в этих условиях равна нулю.
При внесении парамагнетика во внешнее
магнитное поле устанавливается
преимущественная ориентация магнитных
моментов атомов (молекул) в направлении
поля. Таким образом, парамагнетик
намагничивается, создавая собственное
магнитное поле, совпадающее по направлению
с внешним полем и усиливающее его.
Диамагнитный эффект наблюдается и в
парамагнетиках, но он значительно слабее
парамагнитного и поэтому остается
незаметным. Магнитная восприимчивость
парамагнетиков положительна, значительно
меньше единицы и составляет величину ![]() .
В слабом магнитном поле намагниченность
пропорциональна напряженности внешнего
поля. В очень сильном магнитном поле (и
при достаточно низкой температуре)
магнитные моменты всех молекул
располагаются практически параллельно
полю. При этом намагниченность
парамагнетика достигает максимального
значения (но существенно меньшего по
сравнению с ферромагнетиками).
Парамагнетикам соответствует кривая
3.
.
В слабом магнитном поле намагниченность
пропорциональна напряженности внешнего
поля. В очень сильном магнитном поле (и
при достаточно низкой температуре)
магнитные моменты всех молекул
располагаются практически параллельно
полю. При этом намагниченность
парамагнетика достигает максимального
значения (но существенно меньшего по
сравнению с ферромагнетиками).
Парамагнетикам соответствует кривая
3.
Задание n 7 Тема: Сложение гармонических колебаний
Складываются
два взаимно перпендикулярных колебания.
Установите соответствие между номером
соответствующей траектории и законами
колебаний точки ![]() вдоль
осей координат
вдоль
осей координат ![]()
![]()
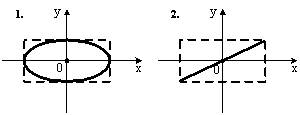
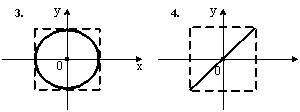
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
|
|
|
|
Решение:
При
одинаковой частоте складываемых
колебаний уравнение траектории точки
имеет вид: 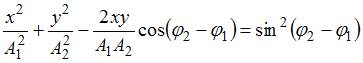 ,
где
,
где ![]() –
разность фаз колебаний. Если разность
фаз
–
разность фаз колебаний. Если разность
фаз ![]() ,
то уравнение преобразуется к виду
,
то уравнение преобразуется к виду 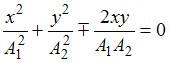 ,
или
,
или 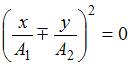 ,
что соответствует уравнению прямой:
,
что соответствует уравнению прямой: 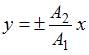 .
Если
.
Если ![]() ,
то
,
то 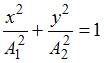 ,
что является уравнением эллипса, причем
если амплитуды равны
,
что является уравнением эллипса, причем
если амплитуды равны ![]() ,
то это будет уравнение окружности.
Если
складываются колебания с циклическими
частотами
,
то это будет уравнение окружности.
Если
складываются колебания с циклическими
частотами ![]() и
и ![]() ,
где
,
где ![]() и
и ![]() целые
числа, точка
описывает
более сложную кривую, которую называют
фигурой Лиссажу. Форма кривой Лиссажу
зависит от соотношения амплитуд, частот
и начальных фаз складываемых колебаний.
целые
числа, точка
описывает
более сложную кривую, которую называют
фигурой Лиссажу. Форма кривой Лиссажу
зависит от соотношения амплитуд, частот
и начальных фаз складываемых колебаний.
ЗАДАНИЕ N 8 Тема: Свободные и вынужденные колебания
На рисунках
изображены зависимости от времени
координаты и ускорения материальной
точки, колеблющейся по гармоническому
закону.
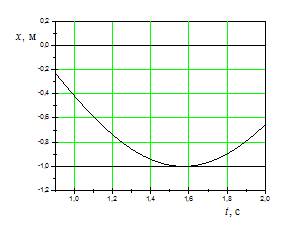
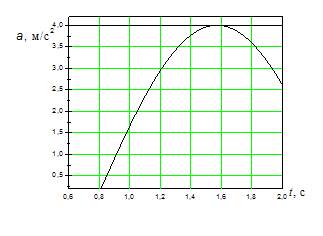 Циклическая
частота колебаний точки равна …
Циклическая
частота колебаний точки равна …
|
2 |
Решение:
Амплитудное
значение ускорения определяется по
формуле ![]() ,
где
,
где ![]() амплитуда
координаты (максимальное смещение
материальной точки),
амплитуда
координаты (максимальное смещение
материальной точки), ![]() циклическая
частота. Используя графики,
находим:
циклическая
частота. Используя графики,
находим: ![]()
![]() ,
, ![]()
![]() Следовательно,
Следовательно, ![]()
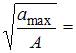
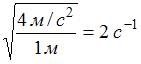 .
.
ЗАДАНИЕ N 9 Тема: Второе начало термодинамики. Энтропия
Если КПД цикла Карно равен 60%, то температура нагревателя больше температуры холодильника в ______ раз(а).
|
|
|
2,5 |
|
|
|
3 |
|
|
|
2 |
|
|
|
1,7 |
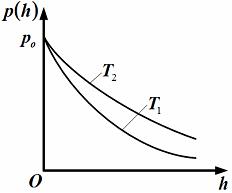
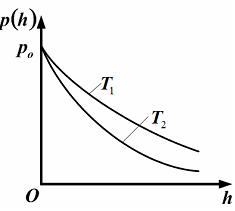
ЗАДАНИЕ N 10 Тема: Распределения Максвелла и Больцмана
Зависимость
давления от высоты для изотермической
атмосферы описывается барометрической
формулой 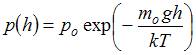 .
Для этой зависимости справедливы
следующие утверждения …
.
Для этой зависимости справедливы
следующие утверждения …
|
|
|
зависимость
давления |
|
|
|
зависимость определяется не только температурой газа, но и массой его молекул |
|
|
|
зависимость
давления
одного
и того же газа при двух разных
температурах
представлена
на рисунке:
|
|
|
|
с
понижением температуры давление газа
на высоте |
Решение:
Из
барометрической формулы следует, что
зависимость давления от высоты
определяется как температурой газа,
так и массой его молекул. Для одного и
того же газа с повышением температуры
зависимость
становится
все более слабо выраженной, так что
молекулы оказываются распределенными
по высоте почти равномерно. При понижении
температуры давление на высотах, отличных
от нуля, убывает, обращаясь в нуль при ![]() .
При этом давление
.
При этом давление ![]() определяется
весом всего газа и не меняется при
изменении температуры. Для разных газов
при одинаковой температуре давление
газа с более тяжелыми молекулами убывает
с высотой быстрее, чем для газа с легкими
молекулами.
определяется
весом всего газа и не меняется при
изменении температуры. Для разных газов
при одинаковой температуре давление
газа с более тяжелыми молекулами убывает
с высотой быстрее, чем для газа с легкими
молекулами.
ЗАДАНИЕ N 11 Тема: Средняя энергия молекул
Молярная
теплоемкость идеального газа при
постоянном давлении равна ![]() где
где ![]() –
универсальная газовая постоянная. Число
вращательных степеней свободы молекулы
равно …
–
универсальная газовая постоянная. Число
вращательных степеней свободы молекулы
равно …
|
|
|
2 |
|
|
|
3 |
|
|
|
1 |
|
|
|
0 |
ЗАДАНИЕ N 12 Тема: Первое начало термодинамики. Работа при изопроцессах
На рисунке
представлена диаграмма циклического
процесса идеального одноатомного
газа:
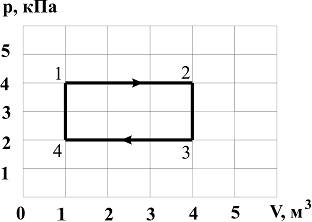 За
цикл газ получает количество теплоты
(в
За
цикл газ получает количество теплоты
(в ![]() ),
равное …
),
равное …
|
33 |
ЗАДАНИЕ N 13 Тема: Динамика поступательного движения
Тело
массой ![]() движется
равномерно по вогнутому мосту со
скоростью
движется
равномерно по вогнутому мосту со
скоростью ![]() .
В нижней точке сила давления тела на
мост вдвое превосходит силу тяжести.
Радиус кривизны моста (в
.
В нижней точке сила давления тела на
мост вдвое превосходит силу тяжести.
Радиус кривизны моста (в ![]() )
равен …
)
равен …
|
10 |
ЗАДАНИЕ N 14 Тема: Динамика вращательного движения
Диск может
вращаться вокруг оси, перпендикулярной
плоскости диска и проходящей через его
центр. К нему прикладывают одну из сил
(![]() ,
, ![]() ,
, ![]() или
или ![]() ),
лежащих в плоскости диска и равных по
модулю.
),
лежащих в плоскости диска и равных по
модулю.
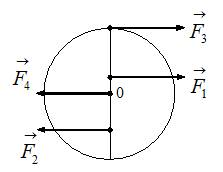 Верным
для угловых ускорений диска является
соотношение …
Верным
для угловых ускорений диска является
соотношение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Согласно
основному уравнению динамики вращательного
движения твердого тела относительно
неподвижной оси угловое ускорение
равно: 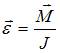 .
Отсюда следует, что угловое ускорение
прямо пропорционально моменту приложенной
к диску силы, который, в свою очередь,
прямо пропорционален величине плеча
силы (при условии равенства модулей
сил). Таким образом,
,
,
так как плечо силы
равно
нулю, и поэтому момент силы
равен
нулю.
.
Отсюда следует, что угловое ускорение
прямо пропорционально моменту приложенной
к диску силы, который, в свою очередь,
прямо пропорционален величине плеча
силы (при условии равенства модулей
сил). Таким образом,
,
,
так как плечо силы
равно
нулю, и поэтому момент силы
равен
нулю.















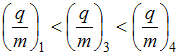


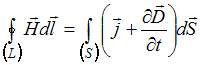
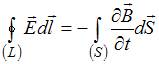
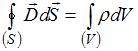
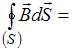 0.
0.