№4.Непрерывность функции в точке. Свойства и теоремы.

Непрерывность функции.

Пусть задана функция z=f(x,y), р (х, у) - текущая точка, р₀(х₀,у₀) - рассматриваемая точка.

Функция z = f(x,y) называется непрерывной в точке р₀, если выполняются 3 условия:

• функция определена в этой точке f(р0) = f(x,y);

• функция имеет предел в этой точке lim f(р) = , p  p0

• предел равен значению функции в этой точке:  = f(x₀,y₀);

lim f(x,y) = f(x₀,y₀), p  p₀

Свойства:

1. Если хотя бы 1 из условий непрерывности нарушается, то точка р называется точкой разрыва. Для функций 2х переменных могут существовать отд. точки разрыва и целые линии разрыва.

2. Понятие предела и непрерывности для функций большего числа переменных определяется аналогично.

3. Функцию трех переменных невозможно изобразить графически, в отличие от функции 2х переменных.

Для функции 3-х переменных могут существовать точки разрыва, линии и поверхности разрыва.

№ 7.Первый замечательный предел.

lim Sinx / x = 1, при х 0

Имеем окружность R = 1 и касательные AD, BD. Из прямоугольных ОАС и ОАD следует: Sin x = AC/1, tg x = AD/1. Точки А и В соединяют три линии: прямая АВ = 2АС = 2 Sin x, дуга АВ = 2х и ломанная ФВИ = 2АD = 2tgx. Из соотношения длин этих линий следует: 2Sinx < 2x < 2tgx. Значит, 1 < x/Sinx < 1/Cosx, 1 > Sinx/x > Cosx. При переходе в неравенстве к пределу х0 имеем lim Cosx =1, 1  lim Sinx/x  1, следовательно, lim Sinx/x = 1.

№8.Число е. Второй замечательный предел.

Натуральное число – основание логарифма, приводящее к высшей степени симметрии графиков показательной и логарифмической функций. Обозначается е = 2,72…

Доказательство второго замечательного предела:

Доказательство второго замечательного предела для случая последовательности (т.е. для натуральных значений x)  

Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, т.е. докажем, что  . Рассмотрим два случая:

1. Пусть  . Каждое значение x заключено между двумя положительными целыми числами:  , где n = [x] - это целая часть x.

Отсюда следует:  , поэтому

.

Если  , то  . Поэтому, согласно пределу  , имеем:

.

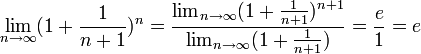
По признаку (о пределе промежуточной функции) существования пределов  .

2. Пусть  . Сделаем подстановку − x = t, тогда

.

Из двух этих случаев вытекает, что   для любого x.    

Следствия

Доказательство следствия

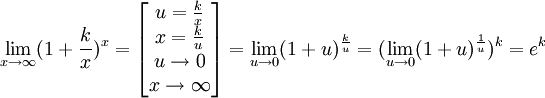
Следствия из второго замечательного предела:

Замечательный логарифмический предел

Доказательство предела

Замечательный показательный предел

Следствия

 для  , 

Доказательство предела

Доказательство следствия

Замечательный степенной предел

Доказательство предела

№9. Порядок переменной, эквивалентность.

П р и м е р  1.  ,  , потому что

.

 

П р и м е р  2.

.

О п р е д е л е н и е . Если для функции   можно подобрать числа   и  , где  , такие, что

,

то говорят, что функция  есть главный степенной член функции   в окрестности точки  .

Правые части соотношений (3) – (7) суть, очевидно, главные степенные члены левых частей при  .

Будем говорить, что   на множестве   имеет порядок   или еще   есть   - большое от   на   и при этом будем писать

 на  ,                                                  (14)

если

,

где   - не зависящая от   положительная константа.

В частности, равенство

 на 

обозначает тот факт, что    ограничена на  .

П р и м е р ы:

1)   на  ;

2)   на  ;

3)   на  .

№10. Производная функции. Задачи, приводящие к понятию производной (задача о мгновенной скорости, задача об угле наклона касательной к кривой).

№11.Основные правила дифференцирования. Таблица производных элементарных функций.

 Производной от функции    называется конечный предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:

, или  .

Геометрически производная представляет собой угловой коэффициент касательной к графику функции   в точке х, то есть  .

Производная есть скорость изменения функции в точке х.

Отыскание производной называется дифференцированием функции.

Основные правила дифференцирования

Пусть  , тогда:

 

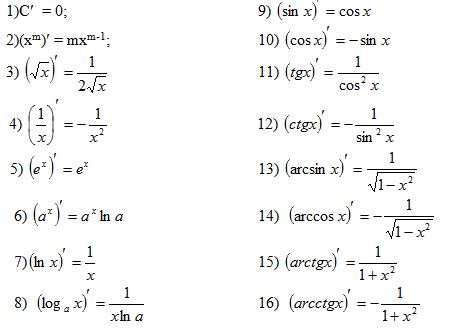
 Дифференцирование неявных функций

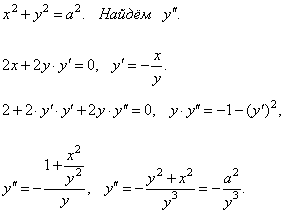
Дифференцирование функций, заданных параметрически

 Дифференцирование функций, заданных параметрически

Пусть функция задана параметрическими уравнениями  ,

тогда  , или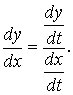 

Приме:

№12. Дифференциал функции. Приближённые вычисления с помощью дифференциала.

Пусть функция у = f(x) имеет производную в точке х, то есть существует предел  , тогда приращение функции можно представить в виде равенства (5) (см. п. 2):

.

Проанализируем его правую часть относительно величины   х, которая будет бесконечно малой, если  . Первое слагаемое является линейным относительно   х, а второе будет бесконечно малой высшего порядка относительно   х.

Определение. Дифференциалом функции у = f(x) называется главная часть приращения функции, линейная относительно приращения   х аргумента и отличающаяся от приращения   у функции на бесконечно малую более высокого порядка, чем  х.

Обозначается:  , (7)

где приращение аргумента  х = dx (в силу его линейности).

Отсюда следует  – формула, которая даёт расшифровку символа производной, формально введённого в п. 1.

Покажем, что формула (7) сохраняет свой вид и в том случае, когда переменная х становится зависимой.

Пусть x =x(t) и  .

Тогда по формуле (7)   при условии, что существуют производные   и  .

Продифференцируем у как сложную функцию аргумента t по формуле (6):

.

Заметим, что  .

Тогда  .

Таким образом, мы получили прежнюю форму дифференциала.

Это замечательное свойство дифференциала сохранять свою форму называется инвариантностью формы дифференциала.

Исследуя далее понятие дифференциала как главной части приращения функции, можно сделать вывод о применении дифференциала в приближённых вычислениях, заменив им приращение функции

                                       (7.1)

или, подробнее,

,  ;  .

Окончательно  . (8)

Получили формулу для приближённого вычисления с точностью до бесконечно малой высшего порядка, чем D х.

План решения задачи приближённого вычисления Если в условии отсутствует запись функции, составить функцию по виду числа. Выбрать начальное условие  , максимально близкое к заданномух, при этом функция должна вычисляться точно, чтобы не увеличить погрешность вычисления. Найти все составляющие формулы (8), а именно, вычислить: а)  ; б) начальное значение функции  ; в) значение производной f '(x0).  Вычислить значение функции f(x) с требуемой точностью.

Если точность вычисления не указана, ответ записывают с тем количеством знаков, с которым заданы условия задачи (промежуточные вычисления производить с количеством знаков, на один превышающим заданную точность). Ответ округлить.

Проиллюстрируем геометрически понятие дифференциала.

П остроим касательную МС к графику функции у=f(x) в выбранной точке   (см. рис. 9), а также секущую  , где точка

также принадлежит графику функции.

Тогда MT =  x – приращение аргумента,

 – приращение ординаты графика функции,

СТ – приращение ординаты касательной,

–  угловой коэффициент касательной,

– угловой коэффициент секущей.

 или  – приращение ординаты касательной (это и есть геометрический смысл дифференциала).

Кроме того, из рис. 9 видно, что, заменяя отрезок   отрезком СТ, мы получаем формулу (8) приближённого вычисления, причём относительная погрешность тем меньше, чем меньше величина  х.

Пример 6. Вычислить приближённо  .

Решение

1) Построим функцию и зададим начальные условия:

,  , тогда  ,  .

2) Найдём все составляющие формулы (8):

,  ,

.

3) Вычислим (с той степенью точности, с которой заданы условия задачи – три верных знака после запятой):

.

Ответ: 0,997.

Дифференциалы основных элементарных функций

1.		5.
2.		6.
3.		7.
4.		8.