§ 191. Поляризация света при отражении и преломлении на границе двух диэлектриков

Если естественный свет падает на границу раздела двух диэлектриков (например, воздуха и стекла), то часть его отражается, а часть преломляется и распространяется во второй среде. Устанавливая на пути отраженного и преломленного лучей анализатор (например, турмалин), убеждаемся в том, что отраженный и преломленный лучи частично поляризованы: при поворачивании анализатора вокруг лучей интенсивность света периодически усиливается и ослабевает (полного гашения не наблюдается!). Дальнейшие исследования показали, что в отраженном луче преобладают колебания, перпендикулярные плоскости падения (на рис. 275 они обозначены точками), в прелом ленном — колебания, параллельные плоскости падения (изображены стрелками).

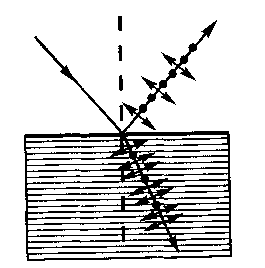
Степень поляризации (степень выделения световых волн с определенной ориентацией электрического (и магнитного) вектора) зависит от угла падения лучей и показателя преломления. Шотландский физик Д. Брюстер (1781—1868) установил закон, согласно которому при угле падения ib (угол Брюстера), определяемого соотношением

(n₂₁ — показатель преломления второй среды относительно первой), отраженный луч является плоскополяризованным (содержит только колебания, перпендикулярные плоскости падения) (рис. 276). Преломленный же луч при угле падения i_B поляризуется максимально, но не полностью.

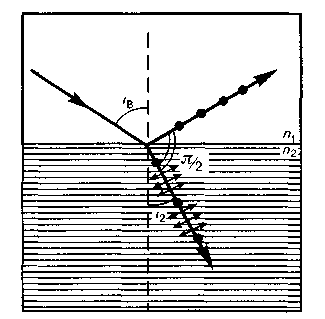
Если свет падает на границу раздела под углом Брюстера, то отраженный и преломленный лучи взаимно перпендикулярны (tgi_B = sini_B/cosi_B, n₂₁ = sini_B / sini₂ (i₂ — угол преломления), откуда cosi_B = sini₂). Следовательно, i_B – i₂ = /2, но i_b = i_B (закон отражения), поэтому i'_B + i₂ = /2.

Двойное лучепреломление в анизотропных средах. Искусственная анизотропия. Метод фотоупругости. Вращение плоскости поляризации.

Двойное лучепреломление

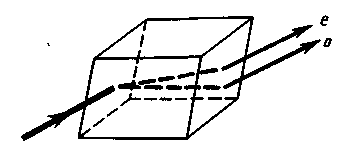
Если на толстый кристалл исландского шпата направить узкий пучок света, то из кристалла выйдут два пространственно разделенных луча, параллельных друг другу и падающему лучу (рис. 277).

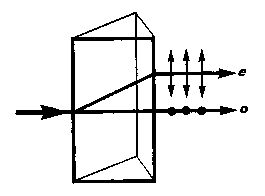
Даже в том случае, когда первичный пучок падает на кристалл нормально, преломленный пучок разделяется на два, причем один из них является продолжением первичного, а второй отклоняется (рис. 278). Второй из этих лучей получил название необыкновенного (е), а первый — обыкновенного (о).

В кристалле исландского шпата имеется единственное направление, вдоль которого двойное лучепреломление не наблюдается. Направление в оптически анизотропном кристалле, по которому луч света распространяется, не испытывая двойного луче преломления, называется оптической осью кристалла. В данном случае речь идет именно о направлении, а не о прямой линии, проходящей через какую-то точку кристалла. Любая прямая, проходящая параллельно данному направлению, является оптической осью кристалла. Кристаллы в зависимости от типа их симметрии бывают одноосные и двуосные, т. е. имеют одну или две оптические оси (к первым и относится исландский шпат).

Исследования показывают, что вышедшие из кристалла лучи плоскополяризованы во взаимно перпендикулярных плоскостях. Плоскость, проходящая через направление луча света и оптическую ось кристалла, называется главной плоскостью (или главным сечением кристалла). Колебания светового вектора (вектора напряженности Е электрического поля) в обыкновенном луче происходят перпендикулярно главной плоскости, в необыкновенном — в главной плоскости (рис. 278).

Неодинаковое преломление обыкновенного и необыкновенного лучей указывает на различие для них показателей преломления. Очевидно, что при любом направлении обыкновенного луча колебания светового вектора перпендикулярны оптической оси кристалла, поэтому обыкновенный луч распространяется по всем направлениям с одинаковой скоростью и, следовательно, показатель преломления n₀ для него есть вели чина постоянная. Для необыкновенного же луча угол между направлением колебаний светового вектора и оптической осью отличен от прямого и зависит от направления луча, поэтому необыкновенные лучи распространяются по различным направлениям с разными скоростями. Следовательно, показатель преломления п_е необыкновенного луча является переменной величиной, зависящей от направления луча. Таким образом, обыкновенный луч подчиняется закону преломления (отсюда и название «обыкновенный»), а для необыкновенного луча этот закон не выполняется. После выхода из кристалла, если не принимать во внимание поляризацию во взаимно перпендикулярных плоскостях, эти два луча ничем друг от друга не отличаются.

Как уже рассматривалось, обыкновенные лучи распространяются в кристалле по всем направлениям с одинаковой скоростью v₀ = c/n₀, а необыкновенные — с разной скоростью v_в =с/n_в. (в зависимости от угла между вектором Е и оптической осью). Для луча, распространяющегося вдоль оптической оси, n₀ = n_e, v₀ = v_e т. е. вдоль оптической оси существует только одна скорость распространения света. Различие в v_e и v_в для всех направлений, кроме направления оптической оси, и обусловливает явление двойного лучепреломления света в одноосных кристаллах.

Допустим, что в точке S внутри одноосного кристалла находится точечный источник света. На рис. 279 показано распространение обыкновенного и необыкновенного лучей в кристалле (главная плоскость совпадает с плоскостью чертежа, ОО' — направление оптической оси).

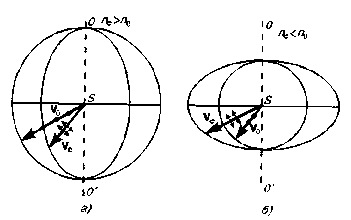
Волновой поверхностью обыкновенного луча (он распространяется с v₀ = const) является сфера, необыкновенного луча (v_e  const) — эллипсоид вращения. Наибольшее расхождение волновых поверхностей обыкновенного и необыкновенного лучей наблюдается в направлении, перпендикулярном оптической оси. Эллипсоид и сфера касаются друг друга в точках их пересечения с оптической осью ОО', Если то v_e < v_о (n_е > n_o), эллипсоид необыкновенного луча вписан в сферу обыкновенного луча (эллипсоид скоростей вытянут относительно оптической оси) и одноосный кристалл называется положительным (рис. 279, а). Если v_e > v₀ (n_e < n₀), то эллипсоид описан вокруг сферы (эллипсоид скоростей растянут в направлении, перпендикулярном оптической оси) и одноосный кристалл называется отрицательным . Рассмотренный выше исландский шпат относится к отрицательным кристаллам.

Двойное лучепреломление имеет место в естественных анизотропных средах (см. § 192). Существуют, однако, различные способы получения искусственной оптической анизотропия, т. е. сообщения оптической анизотропии естественно изотропным веществам.

Оптически изотропные вещества становятся оптически анизотропными под действием: 1) одностороннего сжатия или растяжения (кристаллы кубической системы, стекла и др.); 2) электрического поля (эффект Керра^*; жидкости, аморфные тела, тазы); 3) магнитного поля (жидкости, стекла, коллоиды). В перечисленных случаях вещество приобретает свойства одноосного кристалла, оптическая ось которого со впадает с направлением деформации, электрического или магнитного полей соответственно указанным выше воздействиям.

Мерой возникающей оптической анизотропии служит разность показателей прело мления обыкновенного и необыкновенного лучей в направлении, перпендикулярном оптической оси:

где k₁, k₂, k₃ — постоянные, характеризующие вещество,  — нормальное напряжение, Е и Н — соответственно напряженность электрического и магнитного полей.

Искусственная анизотропия под действием механических воздействий позволяет исследовать напряжения, возникающие в прозрачных телах. В данном случае о степени деформации отдельных участков изделия (например, остаточных деформаций в стекле при закалке) судят по распределению в нем окраски. Так как применяемые обычно в технике материалы (металлы) непрозрачны, то исследование напряжений производят на прозрачных моделях, а потом делают соответствующий пересчет на проектируемую конструкцию.

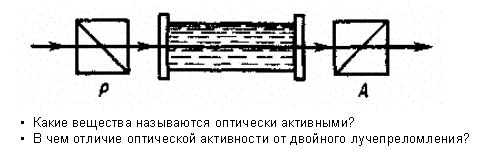
Некоторые вещества (например, из твердых тел — кварц, сахар, киноварь, из жид костей — водный раствор сахара, винная кислота, скипидар), называемые оптически активными, обладают способностью вращать плоскость поляризации.

Вращение плоскости поляризации можно наблюдать на следующем опыте (рис. 285). Если между скрещенными поляризатором Р и анализатором А, дающими темное поле зрения, поместить оптически активное вещество (например, кювету с раствором сахара), то поле зрения анализатора просветляется. При повороте анализатора на некоторый угол  можно вновь получить темное поле зрения. Угол  и есть угол, на который оптически активное вещество поворачивает плоскость поляризации света, прошедшего через поляризатор. Так как поворотом анализатора можно получить темное поле зрения, то свет, прошедший через оптически активное вещество, является плоскополяризованным.

Опыт показывает, что угол поворота плоскости поляризации для оптически активных кристаллов и чистых жидкостей

для оптически активных растворов

где d — расстояние, пройденное светом в оптически активном веществе,  ([]) — так называемое удельное вращение, численно равное углу поворота плоскости поляризации света слоем оптически активного вещества единичной толщины (единичной концентрации — для растворов), С — массовая концентрация оптически активного вещества в растворе, кг/м³. Удельное вращение зависит от природы вещества, температуры и длины волны света в вакууме.

Тепловое излучение

1. Спектральные характеристики теплового излучения. Закон Кирхгофа.

Законы излучения абсолютно черного тела.

Противоречия классической физики. Квантовая гипотеза Планка.

Тела, нагретые до достаточно высоких температур, светятся. Свечение тел, обусловленное нагреванием, называется тепловым (температурным) излучением. Тепловое излучение, являясь самым распространенным в природе, совершается за счет энергии теплового движения атомов и молекул вещества (т. е. за счет его внутренней энергии) и свойственно всем телам при температуре выше 0 К. Тепловое излучение характеризуется сплошным спектром, положение максимума которого зависит от температуры. При высоких температурах излучаются короткие (видимые и ультрафиолетовые) электромагнитные волны, при низких — преимущественно длинные (инфракрасные).

Количественной характеристикой теплового излучения служит спектральная плотность энергетической светимости (излучательностн) тела — мощность излучения с единицы площади поверхности тела в интервале частот единичной ширины:

где dW^изл_{v, dv} — энергия электромагнитного излучения, испускаемого за единицу времени (мощность излучения) с единицы площади поверхности тела в интервале частот от v до v+dv.

Единица спектральной плотности энергетической светимости (R_v,T) — джоуль на метр в квадрате (Дж/м²).

Записанную формулу можно представить в виде функции длины волны:

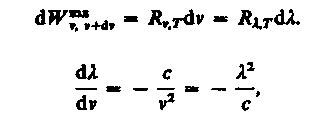
где знак минус указывает на то, что с возрастанием одной из величин (v или ) другая величина убывает. Поэтому в дальнейшем знак минус будем опускать. Таким образом,

С помощью формулы (197.1) можно перейти от R_v,T к R_,T, и наоборот.

Зная спектральную плотность энергетической светимости, можно вычислить интегральную энергетическую светимость (интегральную нзлучательность) (ее называют про сто энергетической светимостью тела), просуммировав по всем частотам:

Способность тел поглощать падающее на них излучение характеризуется спектральной поглощательной способностью

показывающей, какая доля энергии, приносимой за единицу времени на единицу площади поверхности тела падающими на нее электромагнитными волнами с частота ми от v до v+dv, поглощается телом. Спектральная поглощательная способность — величина безразмерная. Величины R_v,T и А_v,T зависят от природы тела, его термодинамической температуры и при этом различаются для излучений с различными частотами. Поэтому эти величины относят к определенным Т и v (вернее, к достаточно узкому интервалу частот от v до v+dv).

Тело, способное поглощать полностью при любой температуре все падающее на него излучение любой частоты, называется черным. Следовательно, спектральная поглощательная способность черного тела для всех частот и температур тождественно равна единице (А^ч_v,T = 1). Абсолютно черных тел в природе нет, однако такие тела, как сажа, платиновая чернь, черный бархат и некоторые другие, в определенном интервале частот по своим свойствам близки к ним.

Кирхгоф, опираясь на второй закон термодинамики и анализируя условия равновесного излучения в изолированной системе тел, установил количественную связь между спектральной плотностью энергетической светимости и спектральной поглощательной способностью тел. Отношение спектральной плотности энергетической светимости к спектральной поглощательной способности не зависит от природы тела; оно является для всех тел универсальной функцией частоты (длины волны) и температуры (закон Кирхгофа):

Для черного тела А^ч_v,T ≡ 1, поэтому из закона Кирхгофа (см. (198.1)) вытекает, что R_v,T для черного тела равна r_v,T. Таким образом, универсальная функция Кирхгофа r_v,T есть не что иное, как спектральная плотность энергетической светимости черного тела. Следовательно, согласно закону Кирхгофа, для всех тел отношение спектральной плотности энергетической светимости к спектральной плотности энергетической светимости к спектральной поглощательной способности равно спектральной плотности энергетической светимости черного тела при той же температуре и частоте.

Австрийский физик И. Стефан (183S—1893), анализируя экспериментальные данные (1879), и Л. Больцман, применяя термодинамический метод (1884), решили эту задачу лишь частично, установив зависимость энергетической светимости Л, от температуры. Согласно закону Стефана — Больцмана,

т. е. энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры;  — постоянная Стефана — Больцмана: ее экспериментальное значение равно 5,6710^-8 Вт/(м² К⁴).

Немецкий физик В. Вин (1864—1928), опираясь на законы термо- и электродинамики, установил зависимость длины волны _max, соответствующей максимуму функции r_,T от температуры Т. Согласно закону смещения Вина,

т. е. длина волны l_max, соответствующая максимальному значению спектральной плотности энергетической светимости r_l,T черного тела, обратно пропорциональна его термодинамической температуре, b — постоянная Вина; ее экспериментальное значение равно 2,910^-3 мК.

Гипо́теза Пла́нка — гипотеза, выдвинутая 14 декабря 1900 года Максом Планком и заключающаяся в том, что при тепловом излучении энергия испускается и поглощается не непрерывно, а отдельными квантами (порциями). Каждая такая порция-квант имеет энергию  , пропорциональной частоте ν излучения:

где h или   — коэффициент пропорциональности, названный впоследствии постоянной Планка. На основе этой гипотезы он предложил теоретический вывод соотношения между температурой тела и испускаемым этим телом излучением — формулу Планка.

Позднее гипотеза Планка была подтверждена экспериментально.

Фотоэлектрический эффект. Фотоны

1. Внешний фотоэффект и его законы. Уравнение Эйнштейна.

Внешним фотоэффектом (фотоэлектронной эмиссией) называется испускание электронов веществом под действием электромагнитных излучений. Электроны, вылетающие из вещества при внешнем фотоэффекте, называются фотоэлектронами, а электрический ток, образуемый ими при упорядоченном движении во внешнем электрическом поле, называется фототоком.

три закона внешнего фотоэффекта.

I. Закон Столетова: при фиксированной частоте падающего света число фотоэлектронов, вырываемых из катода в единицу времени, пропорционально интенсивности света (сила фототока насыщения пропорциональна энергетической освещенности Е_е катода).

II. Максимальная начальная скорость (максимальная начальная кинетическая энергия) фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой v.

III. Для каждого вещества существует красная граница фотоэффекта, т. е. минимальная частота v₀ света (зависящая от химической природы вещества и состояния его поверхности), ниже которой фотоэффект невозможен.

Качественное объяснение фотоэффекта с волновой точки зрения на первый взгляд не должно было бы представлять трудностей. Действительно, под действием поля световой волны в металле возникают вынужденные колебания электронов, амплитуда которых (например, при резонансе) может быть достаточной для того, чтобы электроны покинули металл; тогда и наблюдается фотоэффект. Кинетическая энергия вырываемого из металла электрона должна была бы зависеть от интенсивности падающего света, так как с увеличением последней электрону передавалась бы большая энергия. Однако этот вывод противоречит II закону фотоэффекта. Так как, по волновой теории, энергия, передаваемая электронам, пропорциональна интенсивности света, то свет любой частоты, но достаточно большой интенсивности должен был бы вырывать электроны из металла; иными словами, красной границы фотоэффекта не должно быть, что противоречит III закону фотоэффекта. Кроме того, волновая теория не смогла объяснить безынерционность фотоэффекта, установленную опытами. Таким образом, фотоэффект необъясним с точки зрения волновой теории света.

А. Эйнштейн в 1905 г. показал, что явление фотоэффекта и его закономерности могут быть объяснены на основе предложенной им квантовой теории фотоэффекта. Согласно Эйнштейну, свет частотой v не только испускается, как это предполагал Планк (см. § 200), но и распространяется в пространстве и поглощается веществом отдельными порциями (квантами), энергия которых ₀ = hv. Таким образом, распространение света нужно рассматривать не как непрерывный волновой процесс, а как поток локализованных в пространстве дискретных световых квантов, движущихся со скоростью с распространения света в вакууме. Кванты электромагнитного излучения получили название фотонов.

По Эйнштейну, каждый квант поглощается только одним электроном. Поэтому число вырванных фотоэлектронов должно быть пропорционально интенсивности света (I закон фотоэффекта). Безынерционность фотоэффекта объясняется тем, что передача энергии при столкновении фотона с электроном происходит почти мгновенно.

Энергия падающего фотона расходуется на совершение электроном работы выхода А из металла (см. § 104) и на сообщение вылетевшему фотоэлектрону кинетической энергии mv²_max/2. По закону сохранения энергии,

(203.1)

Уравнение (203.1) называется уравнением Эйнштейна для внешнего фотоэффекта.

Уравнение Эйнштейна позволяет объяснить II и III законы фотоэффекта. Из (203.1) непосредственно следует, что максимальная кинетическая энергия фотоэлектрона линейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности (числа фотонов), так как ни А, ни v от интенсивности света не зависят (II закон фотоэффекта). Так как с уменьшением частоты света кинетическая энергия фотоэлектронов уменьшается (для данного металла А=const), то при некоторой достаточно малой частоте v = v₀ кинетическая энергия фотоэлектронов станет равной нулю и фотоэффект прекратится (III закон фотоэффекта).

2. Объяснить вольтамперную характеристику фотоэффекта. Как изменится вольтамперная характеристика при изменении длины волны падающего света и неизменном световом потоке?

вольт-амперная характеристика фотоэффекта — зависимости фототока /, образуемого потоком электронов, испускаемых катодом под действием света, от напряжения U между электродами. Такая зависимость, соответствующая двум различным освещенностям Е, катода (частота света в обоих случаях одинакова), приведена на рис. 290. По мере увеличения U фототок постепенно возрастает, т. е. все большее число фотоэлектронов достигает анода. Пологий характер кривых показывает, что электроны вылетают из катода с различными скоростями. Максимальное значение тока I_нас — фототок насыщения — определяется таким значением U, при котором все электроны, испускаемые катодом, достигают анода:

где n — число электронов, испускаемых катодом в 1 с.

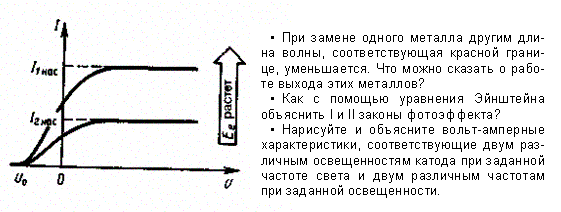
Рис. 290

Из вольт-амперной характеристики следует, что при U = 0 фототок не исчезает. Следовательно, электроны, выбитые светом из катода, обладают некоторой начальной скоростью v, а значит, и отличной от нуля кинетической энергией и могут достигнуть анода без внешнего поля. Для того чтобы фототек стал равным нулю, необходимо приложить задерживающее напряжение U₀. При U = U₀ ни один из электронов, даже обладающий при вылете из катода максимальной скоростью v_max, не может преодолеть задерживающего поля и достигнуть анода. Следовательно,

(202.1)

т. е., измерив задерживающее напряжение U₀, можно определить максимальные значения скорости и кинетической энергии фотоэлектронов.

Энергия и импульс световых фотонов. Эффект Комптона. Давление света.

Согласно гипотезе световых квантов Эйнштейна, свет испускается, поглощается и распространяется дискретными порциями (квантами), названными фотонами. Энергия фотона E₀=hv. Его масса находится из закона взаимосвязи массы и энергии (см. (40.8)):

Фотон — элементарная частица, которая всегда (в любой среде!) движется со скоростью света с и имеет массу покоя, равную нулю. Следовательно, масса фотона отличается от массы таких элементарных частиц, как электрон, протон и нейтрон, которые обладают отличной от нуля массой покоя и могут находиться в состоянии покоя.

Импульс фотона р_ получим, если в общей формуле (40.7) теории относительности положим массу покоя фотона m_0 = 0:

Из приведенных рассуждений следует, что фотон, как и любая другая частица, характеризуется энергией, массой и импульсом. Выражения (205.1), (205.2) и (200.2) связывают корпускулярные характеристики фотона — массу, импульс и энергию — с волновой характеристикой света — его частотой v.

Если фотоны обладают импульсом, то свет, падающий на тело, должен оказывать на него давление. Согласно квантовой теории, давление света на поверхность обусловлено тем, что каждый фотон при соударении с поверхностью передает ей свой импульс.

Рассчитаем с точки зрения квантовой теории световое давление, оказываемое на поверхность тела потоком монохроматического излучения (частота v), падающего перпендикулярно поверхности. Если в единицу времени на единицу площади поверхности тела падает N фотонов, то при коэффициенте отражения  света от поверхности тела N фотонов отразится, a (l - )N — поглотится. Каждый поглощенный фотон передает поверхности импульс р_g = hv/c, а каждый отраженный — 2 р_g = 2hv/c (при отражении импульс фотона изменяется на - р_g). Давление света на поверхность равно импульсу, который передают поверхности в 1 с N фотонов:

Nhv = E_e есть энергия всех фотонов, падающих на единицу поверхности в единицу времени, т.e. энергетическая освещенность поверхности (см. § 168), a

E_e/c = w — объемная плотность энергии излучения. Поэтому давление, производимое светом при нормальном падении на поверхность,

Наиболее полно корпускулярные свойства света проявляются в эффекте Комптона. Американский физик А. Комптон (1892—1962), исследуя в 1923 г. рассеяние монохроматического рентгеновского излучения веществами с легкими атомами (парафин, бор), обнаружил, что в составе рассеянного излучения наряду с излучением первоначальной длины волны наблюдается также более длинноволновое излучение. Опыты показали, что разность ДЯ=Я'—Я не зависит от длины волны Я падающего излучения и природы рассеивающего вещества, а определяется только углом рассеяния в:

(206.1)

где  — длина волны рассеянного излучения, l_C - комптоновская длина волны (при рассеянии фотона на электроне l_C =2,426 пм).

Эффектом Комитета называется упругое рассеяние коротковолнового электромагнитного излучения (рентгеновского и -излучений) на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны. Этот эффект не укладывается в рамки волновой теории, согласно которой длина волны при рассеянии изменяться не должна: под действием периодического поля световой волны электрон колеблется с частотой поля и поэтому излучает рассеянные волны той же частоты.

Атом

1.Закономерности в спектре излучения атома водорода.

Исследования спектров излучения разреженных газов (т. е. спектров излучения отдельных атомов) показали, что каждому газу присущ определенный линейчатый спектр, состоящий из отдельных спектральных линий или групп близко расположенных линий. Самым изученным является спектр наиболее простого атома — атома водорода.

Швейцарский ученый И. Бальмер (1825—1898) подобрал эмпирическую формулу, описывающую все известные в то время спектральные линии атома водорода в видимой области спектра:

(209.1)

где R' = 1,1010⁷ м^-1—постоянная Ридберга^*. Так как v=c/A, то формула (209.1) может быть переписана для частот:

(209.2)

где R = R'с = 3,2910¹⁵ с^-1 — также постоянная Ридбeрга.

Из выражений (209.1) и (209.2) вытекает, что спектральные линии, отличающиеся различными значениями л, образуют группу или серию линий, называемую серией Бальмера. С увеличением л линии серии сближаются; значение n =  определяет границу серии, к которой со стороны больших частот примыкает сплошной спектр.

В дальнейшем (в начале XX в.) в спектре атома водорода было обнаружено еще несколько серий. В ультрафиолетовой области спектра находится серия Лаймана:

В инфракрасной области спектра были также обнаружены:

с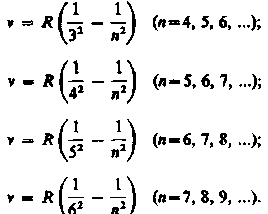 ерия Пашена

серия Брэкета

серия Пфунда

серия Хэмфри

Все приведенные выше серив в спектре атома водорода могут быть описаны одной формулой, называемой обобщенной формулой Бальмера:

(209.3)

где т имеет в каждой данной серии постоянное значение, т= 1, 2, 3, 4, 5, 6 (определяет серию), п принимает целочисленные значения начиная с т+1 (определяет отдельные линии этой серии).

Исследование более сложных спектров — спектров паров щелочных металлов (на пример, Li, Na, К) — показало, что они представляются набором незакономерно расположенных линий. Ридбергу удалось разделить их на три серии, каждая из которых располагается подобно линиям бальмеровской серии.

Приведенные выше сериальные формулы подобраны эмпирически и долгое время не имели теоретического обоснования, хотя и были подтверждены экспериментально с очень большой точностью. Приведенный выше вид сериальных формул, удивительная повторяемость в них целых чисел, универсальность постоянной Ридберга свидетельствуют о глубоком физическом смысле найденных закономерностей, вскрыть который в рамках классической физики оказалось невозможным.

2. Постулаты Бора. Теория Бора для водородоподобных систем.

Первая попытка построить качественно новую — квантовую — теорию атома была предпринята в 1913 г. датским физиком Нильсом Бором (1885—-1962). Он поставил перед собой цель связать в единое целое эмпирические закономерности линейчатых спектров, ящерную модель атома Резерфорда и квантовый характер излучения и поглощения света. В основу своей теории Бор положил два постулата.

Первый постулат Бора (постулат стационарных состояний): в атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергии. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по стационарным орбитам не сопровождается излучением электромагнитных волн.

В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные квантованные значения момента импульса, удовлетворяющие условию

где т, — масса электрона, v — его скорость по n-й орбите радиуса r_n,

ℏ = h/(2).

Второй постулат Бора (правило частот): при переходе электрона с одной стационар ной орбиты на другую излучается (поглощается) один фотон с энергией

равной разности энергий соответствующих стационарных состоянии (Е_n и Е_m — соответственно энергии стационарных состояний атома до и после излучения (поглощения)). При Е_т<Е_п происходит излучение фотона (переход атома из состояния с боль шей энергией в состояние с меньшей энергией, т. с. переход электрона с более удален ной от ядра орбиты на более близлежащую), при Е_т>Е_n— его поглощение (переход атома в состояние с большей энергией, т. е. переход электрона на более удаленную от ядра орбиту). Набор возможных дискретных частот v = (Е_n – Е_m)/h квантовых переходов и определяет линейчатый спектр атома.