6) Аналитическая группировка. Признак-фактор и признак-результат. П2
Аналитическая группировка служит для выявления зависимости между признаками. При этом выделяют признак-фактор и признак-результат. Группировка осуществляется по признаку-фактору. В каждой группе рассчитывается среднее значение признака-результата. Анализируя изменение средних значений признака-результата от группы к группе, можно сделать вывод о наличии или отсутствии взаимосвязи между признаками. Различие групповых средних позволяет утверждать, что признаки взаимозависимы. Если изменение величины признака-фактора в определенном направлении вызывает изменение признака-результата в том же направлении, то говорят, что связь положительная, а в противном случае − отрицательная.
7) Комбинационная группировка по двум признакам и анализ ее результатов на предмет выявления взаимосвязи между признаками. П2
Проследить зависимость между признаками можно также на основе комбинационной группировки, которая осуществляется одновременно по двум признакам.
Если наибольшие числа каждой строки и каждого столбца располагаются вдоль "главной диагонали" таблицы, то можно сделать вывод, что связь положительная и близкая к линейной.
Если наибольшие числа располагаются вдоль другой диагонали таблицы, то можно сделать вывод, что связь отрицательная и близкая к линейной.
Если числа во всех клетках примерно одинаковые, то связи между признаками нет.
8) Дискретный и непрерывный вариационные ряды. Понятие частоты и частости групп. Накопленные частоты (частости) и кумулятивные ряды п 3
Рядами распределения называются числовые ряды, характеризующие структуру совокупности по некоторому признаку. Ряд распределения может быть получен в результате структурной группировки. Ряд распределения, образованный по количественному признаку (вариационный ряд), может быть дискретным (признак принимает ограниченное число возможных значений, например 2,3,4,5) или интервальным (значения признака выражены вещественными числами или число возможных значений признака достаточно велико).
Вариационный ряд оформляется в виде таблицы, где в первой графе указываются варианты (интервалы) значений признака, а в следующих − частота и частость. Ряд распределения в целом характеризует структуру совокупности по данному признаку. Однако могут использоваться и кумулятивные ряды, т.е. ряды накопленных частот (частостей).
Накопленная частота (частость) − это число (доля) элементов совокупности, у которых Накопленная частота на конец i-го интервала определяется по формуле
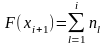значения признака
не превышают данного.
Вариационный ряд можно изобразить в виде графика.
Изображением дискретного ряда является полигон. При его построении по оси абсцисс откладываются варианты (xi), а по оси ординат − частоты или частости − fi. Затем точки с координатами (xi;fi) последовательно соединяются отрезками прямой.
Изображением интервального ряда является гистограмма. При ее построении по оси абсцисс откладываются интервалы ряда. Над осью абсцисс строится прямоугольник, основанием которого является интервал, а высотой − значение частоты или частости.
Изображением ряда накопленных частот является кумулята. Накопленные частоты откладываются по оси ординат для границ интервалов и соединяются отрезками прямых.