26.Способы задания графов.
Геометрический
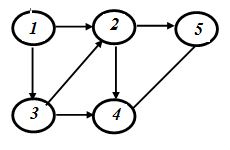
Матрица смежности. Это квадратная матрица порядка п (п – число вершин), в которой нули стоят по главной диагонали (если в графе нет петель, а если петли есть в вершине k (и число этих петель равно р), то на главной диагонали в строчке с номером k стоит число р). Если вершина i связана с вершиной j одним ребром, то элемент матрицы смежности aij равен 1, если эти вершины связаны s ребрами, то аij= s. Аналогичным образом строятся матрицы смежности для орграфов и для мультиграфов.
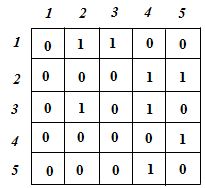
Матрица инциденций – это матрица размера nґ m, где n – число вершин, а m – число ребер графа, при этом ее элементы kij равны 1, если вершина с номером i является для ребра с номером j начальной или конечной (если ребро неориентировано) и начальной для ориентированных ребер.
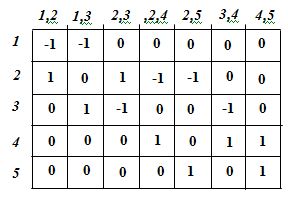
Список пар вершин (см. геометрическое представление графа).
1 – ориентированная ветвь
0 – неориентированная ветвь
Список инцидентности
Во многих случаях лучшим способом описания графов является структура данных, называемая списком инцидентности. Она содержит для каждой вершины, помеченной признаком «начало», список вершин инцидентных, к данной вершине. Каждый список вершин заканчивается признаком «конец». Размерность такой структуры m+n для ориентированного графа и n + 2m для неориентированного графа. Пример:
нач. 1 – 2 – 3 кон.
нач. 2 – 4 – 5 кон.
нач. 3 – 2 – 4 кон.
нач. 4 – 2 – 5 кон. нач. 5 – 4 кон.
27.Определение связности графа методом поиска в глубину.
Алгоритм:
1.Начальную вершину S помещаем в стек
2.Определяем новую вершину смежную с S если такой нет то поиск окончен вершина S не связана с вершиной графа если же S смежна с вершиной vi, то vi помещаем в стек.
3.Определяем новую вершину смежную с последней вершиной помещённой в стек, если вершина есть то добавляем её в стек и повторяем (3), иначе её перемещаем в СИВ, а поиск продолжаем из крайней вершины стека.
4.Выполняем пункт (3)до тех пор пока из стека в СИВ не перейдёт начальная вершина S.
28.Определение связности графа методом поиска в ширину.
Алгоритм:
1.Начальную вершину S помещаем в очередь определённые новые вершины смежные с S если нет, то поиск окончен вершина S несвязанна с другими вершинами графа, если же S смежна в вершине.
2. vi… vj , то эти вершины новые после чего вместе с S перемещаем в СИВ.
3.Из СИВ выбираем следующую вершину за vi и помещаем в очередь, определяем смежные с ней новые вершины и помещаем в список новых и использованных вершин.
Если новых нет то (4).
4.В очередь помещается следующая вершина из СИВ для которой выполняется действие пункта (3).
5.Поиск заканчивается тогда когда в очереди просматривается все вершины из СИВ.
29. Метод построения дерева путей.
Алгоритм:
1.Корню дерева путей образованного вершиной S присваиваем 0-й уровень.
2.Из корня дерева строятся ветви 1-го уровня на концах которых помещаются вершины 1-го уровня смежные с S.
3.Ветви 2-го уровня строят из вершины находятся на 1-м уровне при этом из вершины 1-го уровня выходит столько ветвей со сколькими вершинами графа смежна эта вершина исключая S.
4.Строятся ветви и вершины 3-го и далее аналогично пункту (3) при этом вершина может включаться в уровень если она ранее не встречалась.
5.Конец тогда когда будут охвачены все связи в графе.