15.Отношение толерантности.

Отношением толерантности (или просто толерантностью) на множестве  называется бинарное отношение, удовлетворяющее свойствам рефлексивности и симметричности, но не обязательно являющееся транзитивным. Таким образом, отношение эквивалентности является частным случаем толерантности.

В отличие от отношения эквивалентности, дающего разбиение множества элементов, на котором оно определено, на непересекающиеся подмножества, отношение толерантности даёт покрытие этого множества. Отношение толерантности используется, например, также при классификациях информации в базах знаний.

На содержательном уровне толерантность означает следующее. Любой объект неразличим сам с собой (свойство рефлексивности), а сходство двух объектов не зависит от того, в каком порядке они сравниваются (свойство симметричности). Однако, если один объект сходен с другим, а этот другой — с третьим, то это вовсе не значит, что все три объекта схожи между собой (таким образом, свойство транзитивности может не выполняться).

16.Выборки элементов. Правило суммы и произведения.

Одной из задач комбинаторики является определение количества подмножеств которые можно обрабатывать выборкой элементов из множества по определённым правилам.

Выборка из n элементов называется r перестановкой, если учитывается порядок и учёт.

Выборка из n элементов называется r сочетанием, если не учитывается порядок и учёт.

r – количество элементов

1. Правило суммы: если объект А может быть выбран Р способами, а объект В Q способами, то выбор (либо А или В) может быть выбран Р+Q способами. Следует помнить что А и В должны быть взаимно исключающими т.е. ни 1 из способов выбора элемента А не должен совпадать с выбором элемента В при наличие совпадений общее число уменьается на количество совпадений P+Q-k

2. Правило произведения: Если А выбрать Р способами и после каждого, объект В может быть выбран Q способами, то выбор А и В осуществляется P*Q способами.

17.Перестановки:

1. r – перестановки из n элементов без повторений:

P(n,r)=n(n-1)(n-2)….(n-r+1) - размещения

2. n перестановка из n элементов: P(n,n)=n! - перестановки

3. Перестановки задаваемые спецификацией:

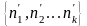
r – перестановки из n элементов с неограниченным числом повторений: U(n,r)=nr

18.Сочетания.

В комбинаторике сочетанием из по называется набор элементов, выбранных из данного множества, содержащего различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

Так, например, наборы (3-хэлементные сочетания, подмножества, ) {2, 1, 3} и {3, 2, 1} 6-тиэлементного множества {1, 2, 3, 4, 5, 6} ( ) являются одинаковыми (однако, как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.

r – сочетания из n элементов без повторений:

r – сочетания из n элементов с неограниченным числом повторений:

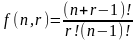f(n,r)=C(n+r-1,r)