9.Подстановки

Взаимно однозначное отображение множества

х={ 1,2,..,n} на себя называют подстановкой n чисел или n-ой степени.

тождественная подстановка n-ой степени e переводит сам в себя. Всякую подстановку можно на произведение циклов множество элементов, которые попарно не пресекаются.

10.Способы представления отношений:

1. Фактор множества: пусть задано отношение AcX×Y Сечение А(хi) называется множество 2-х координат которые находятся в отношении с элементом хi . Множество всех сечений отношения А называют Фактор множества Y по отношению А.

2. Матрица отношений: с – столбцы, yj – строки, ставится 1 если хi ставится в соответствие yj

3. Граф отношения: G(V,E), где V – вершины, E – рёбра. В графе отношения вершины соответствуют элементам множеств участвующих в отношениях, а рёбра(дуги) соединяют те вершины элементы которых связаны данным отношением.

11.Опреации над отношениями

1. Симметризация – отношение обратное некоторому отношению А и обозначается А-1 (перестановка координат (x,y)=(y,x))

2. Композиция

12.Свойства отношений:

Рефлексивно если есть все (1,1), (2,2) ,(3,3)

Антирефлексивно если нет ни одного (1,1), (2,2) ,(3,3)

Симметрично если есть все (1,2), (2,1), (3,2), (2,3)

Ассиметрично если нет ни одного (1,2), (2,1) и нет (1,1), (2,2) ,(3,3)

Антисимметрично если нет ни одного (1,2), (2,1) но есть (1,1), (2,2) ,(3,3)

Транзитивно если композиция такая же.

Если отношение рефлексивно, симметрично и транзитивно, то оно называется отношением эквивалентности.

Если отношение антирефлексивно, асимметрично и транзитивно, то оно называется отношением строгого порядка.

Если отношение рефлексивно, антисимметрично и транзитивно, то оно называется отношением нестрогого порядка.

13.Отношение эквивалентности

представляет собой перевод интуитивных понятий о сходстве и неразличимости строгих математических понятий отношения ~ обладает свойствами : рефлексивности,симметричности, транзитивности. Вознесшие свойство отношения эквивалентности состоит в том что оно определяет признак который допускает разбиение множества М на а подмножестве непересекающихся между собой , они называются классами эквивалентности

14.Отношение порядка.

Бинарное отношение на множестве называется отношением порядка, или отношением частичного порядка, если имеют место

• Рефлексивность:

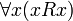
• Транзитивность: ;

• Антисимметричность: .

Множество , на котором введено отношение частичного порядка, называется частично упорядоченным.

Отношение , удовлетворяющее условиям рефлексивности, транзитивности, антисимметричности также называют нестрогим, или рефлексивным частичным порядком и обычно обозначают символом . Если условие рефлексивности заменить на условие антирефлексивности:

,

то получим определение строгого, или антирефлексивного частичного порядка, обозначаемое обычно символом . В общем случае, если  — транзитивное, антисимметричное отношение, то

 — рефлексивный порядок

 — антирефлексивный порядок.

Отношение частичного порядка называется линейным порядком, если выполнено условие

Множество , на котором введено отношение линейного порядка, называется линейно упорядоченным, или цепью.

Отношение , удовлетворяющее только условиям рефлексивности и транзитивности, называется квазипорядком, или предпорядком.