№1

4. Хвильова функція означена з точністю до довільного множника у формі , де - будь-яке дійсне число. Підстановка функції

не міняє середніх значень спостережуваних фізичних величин.

вильова функція квантової системи, що складається з кількох частинок, залежить від координат всіх частинок. Наприклад, для двох частинок  . При визначенні середніх значень спостережуваних величин інтегрування проводиться у всьому конфігураційномі просторі. Наприклад, для двох частинок

У випадку тотожності частинок, на хвильову функцію накладається додаткова умова, пов'язана з інваріантністю щодо перестановок цих частинок, згідно з принципом нерозрізнюваності. Квантові частинки поділяються на два класи - ферміони й бозони. Для ферміонів

,

тобто хвильова функція міняє знак при перестановці частинок. Таку фунцію називають антисиметричною щодо перестановок. Для бозонів

,

тобто при перестановці частинок хвильова функція залишається незмінною. Таку функцію називають симетричною щодо перестановок.

В координатному представленні хвильова функція   залежить від координат (або узагальнених координат) системи. Фізичний сенс приписується квадрату її модуля   , Який інтерпретується як щільність ймовірності   (Для дискретних спектрів - просто ймовірність) виявити систему в положенні, описуваному координатами   в момент часу   :

 .

Тоді в заданому квантовому стані системи, описуваному хвильовою функцією   , Можна розрахувати ймовірність   того, що частка буде виявлена ​​в будь-якій області простору кінцевого обсягу   :   .

Слід також зазначити, що можливо вимірювання і різниці фаз хвильової функції, наприклад, в досвіді Ааронового - Бома.

№2

3. Аналізуючи можливості вимірювання координати й імпульсу квантового об'єкта (наприклад, електрона), Гейзенберг стверджував: неможливо одночасно і до того ж точно виміряти координату й імпульс. Беручи до уваги формулу де Бройля

це означає: не можна одночасно й у той же час точно визначити положення х атомного об'єкта й довжину його хвилі X. Отже, одночасне використання понять "частинка" й "хвиля" є обмеженим. Чисельно таке обмеження виражає нерівність — співвідношення невизначеностей:

Одночасно визначити і координату, і імпульс частинки не можна точніше, ніж це допускає співвідношення невизначеностей. Чим точніше задано координату, тобто чим менше  , тим менш точно можна задати імпульс, тому що величина   обернено пропорційна  . І навпаки, чим точніше задано імпульс частинки, тим гірше визначено її координату.

Обмеження, які встановлює співвідношення невизначеностей, є незмінним законом природи і ніяк не пов'язані з недосконалістю наших приладів. Посилання на всемогутність науки тут є недоречними; сила науки полягає не в тому, щоб порушувати закони природи, а в тому, щоб відкрити їх, зрозуміти й використовувати.

4. Досліди Комптона показали, що довжина хвилі розсіяного випромінювання більша за довжину хвилі 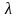падаючого випромінювання, причому різниця 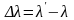не залежить від довжини хвилі падаючого випромінювання і природи розсіювальної речовини, а визначається лише величиною кута розсіяння :

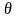Пояснити ефект Комптона можна на основі квантових уявлень про природу світла. Якщо вважати, що випромінювання є потоком фотонів, то ефект Комптона це результат пружного зіткнення рентгенівських фотонів з вільними електронами речовини (для легких атомів електрони слабо зв'язані з ядрами атомів, тому їх можна вважати вільними). У процесі цього зіткнення фотон передає електрону частину своїх енергії й імпульсу відповідно до законів їх збереження.

№3

1. Зовнішнім фотоефектом (фотоелектронною емісією) називається вивільнення електронів речовиною під дією світла. Електрони, які вилітають із речовини при зовнішньому фотоефекті, називаються фотоелектронами, а електричний струм, утворений, ними при впорядкованому русі у зовнішньому електричному полі, называется фототоком.

Закони: Кількість фотоелектронів прямо пропорційна інтенсивності світла.

Максимальна кінетична енергія фотоелектронів не залежить від інтенсивності світла, кінетична енергія фотоелектронів прямо пропорційна частоті світла.

Для кожної речовини існують порогові значення частоти та довжини хвилі світла, які відповідають межі існування фотоефекту; світло з меншою частотою та більшою довжиною хвилі фотоефекту не викликає.

4. Бо́ровская моде́ль а́тома (Моде́ль Бо́ра) — полуклассическая модель атома, предложенная Нильсом Бором в 1913 г. За основу он взял планетарную модель атома, выдвинутую Резерфордом. Однако, с точки зрения классической электродинамики, электрон в модели Резерфорда, двигаясь вокруг ядра, должен был бы излучать непрерывно, и очень быстро, потеряв энергию, упасть на ядро. Чтобы преодолеть эту проблему Бор ввел допущение, суть которого заключается в том, что электроны в атоме могут двигаться только по определенным (стационарным) орбитам, находясь на которых они не излучают, а излучение или поглощение происходит только в момент перехода с одной орбиты на другую. Причем стационарными являются лишь те орбиты, при движении по которым момент количества движения электрона равен целому числу постоянных Планка^[1]:  .

Используя это допущение и законы классической механики, а именно равенство силы притяжения электрона со стороны ядра и центробежной силы, действующей на вращающийся электрон, он получил следующие значения для радиуса стационарной орбиты   и энергии   находящегося на этой орбите электрона:

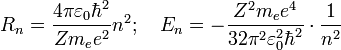
Здесь   — масса электрона, Z — количество протонов в ядре,   — диэлектрическая постоянная, e — заряд электрона.

Именно такое выражение для энергии можно получить, применяя уравнение Шрёдингера, решая задачу о движении электрона в центральном кулоновском поле.

два постулати:

1. Атом або система атомів може знаходитись не в усіх станах, що дозволяє класична механіка, а тільки в деяких певних (надалі - квантових) станах, що мають дискретні значення енергії Е₁, Е₂, Е₃ тощо. В цих станах атом не випромінює. Усі можливі такі стани назвемо стаціонарними.

2. При переході зі стаціонарного стану з енергією Е_n2 до стаціонарного стану з енергією En1, енергія атома змінюється на Е_n2 - E_n1. Якщо такий перехід вввідбувається внаслідок випромінювання (поглинання)¹, то при цьому випускається (поглинається) один фотон з енергією

h = En2 – En1

№4

1. Якщо гамільтоніан квантової системи не зажить від часу, рівняння Шредінгера можна розв'язати відносно часу методом розділення змінних і отримати так зване стаціонарне рівняння Шредінгера

,

де E — певне дійсне число, яке інтерпретують, як енергію. Це рівняння є рівнням на власні значення. Розв'язуючи його знаходять енергетичний спектр квантової системи, тобто такі значення E, при яких розв'язок існує. Кожному власному значенню   стаціонарного рівняння Шредінгера відповідає власна фукнція  .

Загальний розв'язок часового рівняння Шредінгера тоді записується у вигляді:

,

де   — комплексні коефіцієнти, які можна визначити з початкових умов.

У разі, коли гамільтоніан квантової системи залежить від часу, наприклад, при взаємодії системи з електромагнітною хвилею, перехід до стаціонарного рівняння Шредінгера неможливий. В такій квантовій системі енергія не зберігається, система може поглинати енергію хвилі або віддавати її хвилі.