3 билет

Способы определения истиной длины отрезка прямой и углов ее наклона

Определить длину отрезка AВ и угол его наклона к плоскости проекций можно способом введения новых плоскостей прокций. Если отрезок общего положения параллелен какой-либо плоскости, то очевидно, что он проецируется на нее в натуральную величину. Поэтому для решения этой задачи нам нужно ввести дополнительную плоскость проекций П₄ так, чтобы она была параллельна нашему отрезку. Плоскость П₄ может быть перпендикулярной к П₁ либо П₂, от этого зависит лишь угол наклона к какой плоскости проекций мы сможем определить. На рисунке П₄ перпендикулярна П₁.

Нажмите на картинку для просмотра...

Алгоритм графических построений: Проводим ось проекций П1П4 параллельно A1B1 и на произвольном расстоянии от A1B1; Проводим линии проекционной связи в системе плоскостей проекции П1П4 перпендикулярно оси П1П4; Откладываем на них от оси П1П4 расстояния равные расстояниям от А2 и B2 до оси П1П2; Соединяем А4 и B4.  Длина проекции А4B4 равна длине отрезка АВ. Угол  - угол наклона А4B4 к оси П1П4 равен углу наклона АВ к плоскости проекции П1.

 Если нам требуется найти угол наклона отрезка AB к плоскости П₂, то дополнительную плоскость проекций П₄ следует вводить перпендикулярно П₂. Все построения аналогичны, только выполняются они в верхней части чертежа. Естественно, что искомая длина отрезка AB будет одинакова в обоих случаях.

Привести примеры

4 Билет

способы определения углов наклона прямой к плоскостям проекций

З а д а ч а  7. Определить угол наклона плоскости треугольника ABC к плоскостям проекций П₁ и П₂

Порядок решения задачи: проводим линии наибольшего наклона плоскости и способом прямоугольного треугольника определяем углы наклона этих прямых к плоскостям П₁ и П₂.

         Линии наибольшего наклона – это линии, лежащие в заданной плоскости и перпендикулярные линиям уровня (горизонтали или фронтали) или следам плоскости.

         П р и м е р. Дана плоскость треугольника АВС. Определить угол наклона треугольника АВС к плоскости П₁

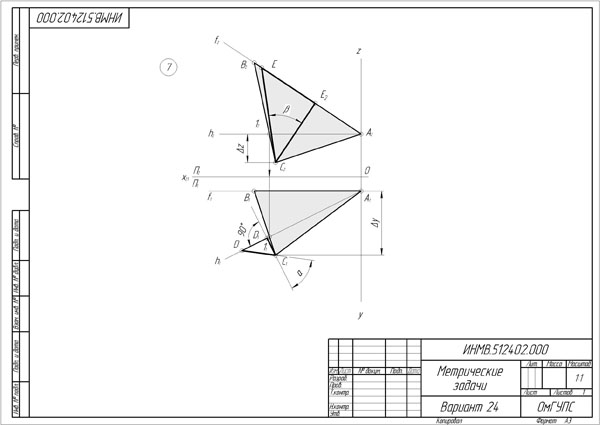
         В плоскости треугольника ABC проводим горизонталь h и из точки С опускаем перпендикуляр к горизонтали, т. е. линию наибольшего наклона к плоскости П₁.

Способом прямоугольного треугольника определяем натуральную величину отрезка СD.       

Угол между натуральной величиной отрезка СD и его горизонтальной проекцией является углом наклона АВС к плоскости П₁ (a).

Угол между натуральной величиной отрезка и его фронтальной проекцией линии наибольшего наклона к плоскости П₂ является углом наклона АВС к плоскости П₂ (b

5 Билет

Проекции плоских углов.Проекции прямого угла.Перпендикуляр к плоскости

Угол - геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки.

Углом между прямыми называется меньший из двух смежных углов, лучи которых параллельны этим прямым.

Углом между плоскостью и не перпендикулярной ей прямой называется угол между прямой и её проекцией на данную плоскость.

Рассмотрим ряд свойств ортогональных проекций плоских углов:

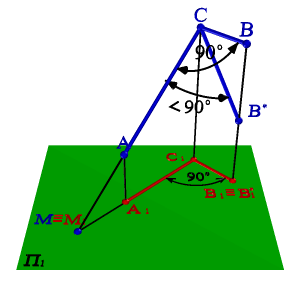
1. Если хотя бы одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то на эту плоскость прямой угол проецируется без искажения (Теорема о проецировании прямого угла).

Рисунок 39. Теорема о проецировании  прямого угла			Рисунок 40. Обратная теорема о проецировании  прямого угла

Дано:  АВС = 90^о; [ВС] // П₁; [АС]  П₁.

Для доказательства теоремы продлим отрезок АС до пересечения с плоскостью П₁ (рис. 39) получим горизонтальный след прямой -  точку М  М₁, одновременно принадлежащую прямой и ее проекции. Из условия следует, что [ВС] // [В₁С₁]. Если через точку М проведем прямую  МD параллельную С₁В₁ , то она будет параллельна и СВ, а следовательно  СМD= 90^о. Согласно теореме о трех перпендикулярах  С₁МD=90^о. Таким образом, [MD][А₁С₁] и [MD]//[В₁С₁], следовательно,  А₁С₁В₁= 90^о, что и требовалось доказать.  В случае, когда [АС]П₁ проекцией угла, согласно свойствам ортогонального проецирования, будет прямая линия.

2. Если проекция угла представляет угол 90⁰, то проецируемый угол будет прямым лишь при условии, что одна из сторон этого угла параллельна плоскости проекций (рис. 40).

3. Если обе стороны любого угла параллельны плоскости проекций, то его проекция равна по величине проецируемому углу. 

4. Если стороны угла параллельны плоскости проекций или одинаково наклонены к ней, то деление проекции угла на этой плоскости пополам соответствует делению пополам и самого угла в пространстве.

5. Если стороны угла не параллельны плоскости проекций, то угол на эту плоскость проецируется с искажением

Проекии прямого угла

Любой линейный угол (острый, тупой, прямой) проецируется на плоскость проекций в истинную величину, если его стороны параллельны этой плоскости. При этом вторая проекция угла вырождается в прямую линию, перпендикулярную линиям связи. Кроме того, прямой угол проецируется в истинную величину еще и тогда, когда только одна из его сторон параллельна плоскости проекций. Теорема 1.  Если одна сторона прямого угла параллельна плоскости проекций, а другая является прямой общего положения, то прямой угол проецируется на эту плоскость проекций без искажения, т. е. в прямой же угол. Пусть стороны (АВ) и (ВС) прямого угла АВС параллельны горизонтальной плоскости проекций П₁ (рис. 4.10). Тогда на П₁ 

< ABC   < A₁B₁C₁ и < A₁B₁C₁ = 90^o

Р 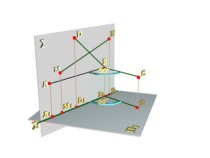ис. 4.10

Сторона (АВ) и ее горизонтальная проекция (А₁В₁) располагаются в горизонтально проецирующей плоскости  ( ₁). Сторона (ВС)    , так как (ВС)   (АВ) по условию и (ВС)   (ВВ₁) по построению. Следовательно, прямая (ВС) перпендикулярна к любой прямой (пересекающейся или скрещивающейся с ней), принадлежащей плоскости  , например: (ВС)   (ВD), (ВС)  (МN) и т. п. (прямые (ВD), (МN), ... общего положения). Очевидно, что проекция на плоскость П₁ прямого угла, образованного прямой (ВС) с любой прямой общего положения, например (ВD), принадлежащей плоскости  , совпадает с проекцией А₁В₁С₁ угла АВС. Таким образом, теорема доказана. Прямой угол DВС на плоскость П₂ проецируется в искаженную величину, так как по отношению к ней условия теоремы не выполняются. Если сторона (ВD) прямого угла DВС займет положение, перпендикулярное плоскости П₁, то проекция угла на эту плоскость выродится в прямую линию, а на две другие плоскости проекций прямой угол спроецируется без искажения.  Р 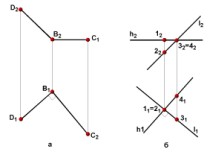ис. 4.11

Проекции прямого угла DВС, сторона (ВС) которого параллельна плоскости П₁, изображены на рис. 4.11, а. На чертеже (рис. 4.11, б) показаны проекции взаимно перпендикулярных скрещивающихся прямых, одна из которых является горизонталью. На чертеже (рис. 4.12, а) показаны проекции прямого угла DВС, сторона (ВС) которого параллельна плоскости П₂. Проекции взаимно перпендикулярных скрещивающихся прямых, одна из которых является фронталью, изображены на чертеже (рис. 4.12, 6). Р 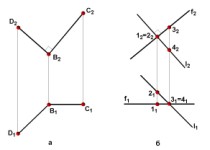ис. 4.12

Перпеникуляр к плоскости

Пусть даны плоскость и не лежащая на ней точка.

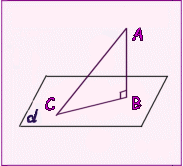
Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра. Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.	Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной.
Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной.

На рисунке из точки А проведены к плоскости  перпендикуляр АВ и наклонная АС. Точка В - основание перпендикуляра, точка С - основание наклонной, ВС - проекция наклонной АС на плоскость  . Смотри также опорную задачу №3.
Теорема 4 О ТРЕХ ПЕРПЕНДИКУЛЯРАХ. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной.  И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Примеры