15) Полярная система координат

Полярная система координат — система координат, ставящая в соответствие каждой точке на плоскости пару чисел .

Основными понятиями этой системы являются точка отсчёта (полюс) и луч, начинающийся в этой точке (полярная ось).

Координата ρ определяет расстояние от точки до полюса, координата — угол между полярной осью и отрезком, соединяющим полюс и рассматриваемую точку.

Координата берётся со знаком «+», если угол от оси до отрезка вычисляется против часовой стрелки, и со знаком «-» в противоположном случае.

Любая точка в этой системе имеет бесконечное число координат вида , которым соответствует одна и та же точка при любых целых n. Для полюса ρ = 0, а угол произвольный.

Иногда допускаются отрицательные значения ρ, в этом случае координаты и определяют одну и ту же точку плоскости.

16. Рівняння прямої на площині

(загальне, канонічне, параметричне, з кутовим коефіцієнтом).

1. Загальне рівняння прямої. Доведемо, що якщо на площині π фіксована довільна декартова прямокутна система Оху, то будь-яке рівняння першої степені з двома змінними х та у визначає відносно цієї системи пряму лінію. Нехай фіксована довільна декартова прямокутна система Оху і задано рівняння першої степені Ах + Ву + С = 0, де А, В, С – будь-які сталі, але із сталих А і В хоча б одна ≠ 0. Це рівняння має хоча б один розв̛ язок, так що існує точка М₀(х₀,у₀), координати якої задовольняють рівняння: Ах₀ + Ву₀ + С = 0. Віднявши від першого друге рівняння отримуємо: А(х-х₀) + В(у-у₀) + С = 0. Якщо точка М(х,у) лежить на вказаній прямій, то її координати задовольняють третє рівняння, в цьому випадку вектори n={A, B} і М₀М={х-х₀, у-у₀} ортогональні і їх скалярний добуток = 0. Якщо ж точка М(х,у) не лежить на вказаній прямій, то її координати не задовольняють рівняння, в цьому випадку вектори n і М₀М не ортогональні і їх скалярний добуток ≠ 0.

2. Канонічне рівняння прямої. Будь-який ненульовий вектор, паралельний даній прямій наз. направляючим вектором цій прямій. Знайдемо рівняння прямої, яка проходить через дану точку М₁(х₁,у₁) і заданий направляючий вектор q={a,b}. Точка М(х,у) лежить на вказаній прямій тоді і тільки тоді, коли вектори М₁М={х-х₁, у-у₁} і q={a,b} колінеарні, таким чином координати цих векторів пропорційні: (х-х₁)/а = (у-у₁)/ b.

3. Параметрине рівняння прямої. Параметричне рівняння прямої слідує з канонічного. Візьмемо за параметр величину t, який стоїть в лівій і правій частинах канонічного рівняння. Так як один із знаменників ≠ 0, а відповідний чисельник може мати будь-яке значення, то область визначення параметра: -∞<t<+∞. Ми отримуємо х-х₁=а t, у-у₁= bt => х=х₁+а t, у=у₁+bt.

4. Пряма з кутовим коефіцієнтом. Розглянемо будь-яку пряму, не паралельну осі Ох. Введемо поняття кута нахилу цієї прямої до осі Ох. Припустимо, що пряма перетинає вісь Ох в точці А. Візьмемо на осі Ох довільну точку М, яка лежить по іншу сторону від точки А, куди прямує вісь Ох, а на прямій довільну точку N, яка лежить по іншу сторону від точки А, куди прямує вісь Оу. Кут α – кут нахилу даної прямої до осі Ох. Тангенс кута нахилу прямої до осі Ох назвемо кутовим коефіцієнтом цієї прямої. K=tgα. Виведемо рівняння прямої, яка проходить через дану точку М₁(х₁,у₁) і даний кутовий коефіцієнт к. Для цього докажемо, що пряма не паралельна осі Оу і яка має направляючий вектор q={a,в}, то кутовий коефіцієнт цієї прямої дорівнює k=в/a. Нехай α – кут нахилу прямої до осі Ох, а β – кут нахилу направляючого вектора q={a,в} до осі Ох. Так як пряма може бути нахилена до осі Ох під гострим кутом або під тупим кутом і її направляючий вектор q може мати два протилежних напрямки. Коли α=β, то a=|q|cosβ, в=|q|sinβ => tgβ=tgα, в/a=tgβ . Коли β=π-α, то a=|q|cosβ, в=-|q|sinβ => tgβ=-tgα, в/a=-tgβ. Бачимо, що в усіх випадках в/a=tgα. Для того щоб вивести рівняння прямої, яка проходить через задану точку М₁(х₁,у₁) і кутовий коефіцієнт к, помножимо дві частини канонічного рівняння на в, враховуючи що к=в/а, отримаємо: у-у₁=к*(х-х₁), позначимо, що b=у₁–кх₁ , тоді маємо у = кх + b.

1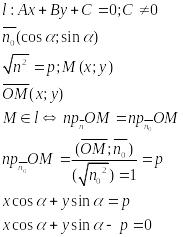 0)Нормальне рівняння прямої.

11)

Відстань от точки до прямой

Теорема. Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как

. Доказательство. Пусть точка М1(х1, у1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1:

К оординаты x1 и у1 могут быть найдены как решение системы уравнений:

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М0 перпендикулярно заданной прямой.

Если преобразовать первое уравнение системы к виду:

A(x – x0) + B(y – y0) + Ax0 + By0 + C = 0,

то, решая, получим:

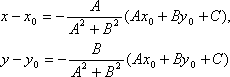
Подставляя эти выражения в уравнение (1), находим: .

Теорема доказана.

12. Криві другого порядку (еліпс,гіпербола,парабола). Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

в котором по крайней мере один из коэффициентов отличен от нуля.

Еліпс – геометричне місце точок площини, таких, що сума відстаней від кожної з цих точок до двох фіксованих точок (фокусів) є сталою. | F1M | + | F2M | = 2a. X^2/a^2 + Y^2/b^2 = 1 – канонічне рівняння.

Гіпербола – геометричне місце точок таких, що модуль різниці відстаней від кожної з них до двох фокусів є сталою. X^2/a^2 – Y^2/b^2 =1.

Парабола – геометричне місце точок таких, що відтань від кожної з яких від фіксованої точки (фокуса) до фіксованої прямої (директриси) є однаковою. Y^2=2px.