8. Задача линейного программирования (постановка и формы записи задач линейного программирования).

Линейное программирование является одной из основных частей того раздела современной математики, который получил название математического программирования. В общей постановке задачи этого раздела выглядят следующим образом.

Имеются какие-то переменные и функция этих переменных , которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции при условии, что переменные x принадлежат некоторой области G:

В зависимости от вида функции и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Подробнее об этом будет сказано в заключении.

Линейное программирование характеризуется тем, что

а) функция является линейной функцией переменных ;

б) область G определяется системой линейных равенств или неравенств.

9. Методы решения задач линейного программирования и их классификация.

- Графический метод

- Симплексный метод

- Двойственный симплекс метод

10. Геометрическая интерпретация задач линейного программирования (особенности и свойства данной задачи описывать обязательно).

Рассмотрим случай, когда число переменных n на два больше, чем число независимых уравнений т, которым они должны удовлетворять:

n - m = 2.

Тогда можно две из п переменных, скажем и выбрать в качестве свободных, а остальные т сделать базисными и выразить их через свободные. Предположим, что это сделано. Получим m = n - 2 уравнений вида:

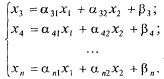(2.17)

Дадим задаче линейного программирования геометрическую интерпретацию. По осям и будет откладывать значения свободных переменных (рис. 2.5, б).

Так как переменные должны быть неотрицательными, допустимые значения свободных переменных лежат только выше оси и правее оси ; отметим это штриховкой, обозначающей «допустимую сторону» каждой координатной оси.

Остальные переменные также должны быть неотрицательными, т. е. должны выполняться условия:

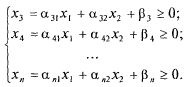
Посмотрим, как изобразить эти условия геометрически. Возьмем одно из них, например, первое:

Положим величину равной своему крайнему значению — нулю. Получим уравнение

Это уравнение прямой линии. На этой прямой (см. рис. 2.5, б); по одну сторону от нее (отмечено штриховкой), по другую —

Аналогично могут быть построены все остальные ограничивающие прямые: (рис. 2.5). Штриховкой отмечено, где соответствующая переменная больше нуля.

Таким образом, мы получили п прямых: две оси координат и n - 2 прямых Каждая из них определяет «допустимую полуплоскость», лежащую по одну ее сторону. Часть плоскости принадлежащая одновременно всем этим полуплоскостям, образует область допустимых решений (ОДР). На рис. 2.5, б область допустимых решений отмечена более темной штриховкой.

Нетрудно убедиться, что область допустимых решений всегда представляет собой выпуклый многоугольник. Как известно, выпуклой (рис. 2.5, б) называется фигура, обладающая следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ также принадлежит ей.

Таким образом, мы рассмотрели вопрос о существовании области допустимых решений ОЗ и (для случая m = n - 2) дали ему геометрическую интерпретацию.

Теперь возникает вопрос о нахождении из числа допустимых оптимального решения, т. е. такого, которое обращает в минимум линейную функцию (2.14)

Дадим и этой задаче геометрическую интерпретацию, причем снова для случая, когда m = n - 2 (т. е. число свободных переменных равно 2, а число базисных — m).

Предположим, что опять свободными переменными являются а базисными —выраженные через свободные формулами (2.17). Подставим выражения (2.17) в (2.14), приведем подобные члены и выразим линейную функцию Z вcex и переменных как линейную функцию только двух свободных переменных — Получим:

(2.18)

где — свободный член, которого в первоначальном виде у функции Z не было.

Очевидно, линейная функция (2.18) достигает минимума при тех же значениях что и функция

без свободного члена (линейная форма).

Найдем эти значения, пользуясь геометрической интерпретацией. Если придать Z' некоторое постоянное значение С, то получим уравнение прямой на плоскости (рис. 2.5, б). Угловой коэффициент этой прямой равен а отрезок, отсекаемый ею на оси (начальная ордината), равен Таким образом, различным значениям Z' соответствуют разные прямые на плоскости, но все они параллельны между собой. Очевидно, вместо всех этих прямых достаточно изобразить на плоскости одну основную прямую, например, а затем можно мысленно перемещать ее параллельно себе. При перемещении этой прямой в одну сторону Z' будет возрастать, в другую — убывать. Дадим теперь геометрическую интерпретацию нахождения оптимального решения ОЗ среди допустимых.

При перемещении основной прямой в направлении к началу координат линейная форма Z' будет убывать. Очевидно, наименьшего значения она достигнет, когда прямая будет проходить через крайнюю точку ОДР. Координаты этой точки и определяют оптимальное решение ОЗ. Зная оптимальные значения свободных переменных можно найти, подставляя их в уравнения (2.17), и оптимальные значения базисных переменных:

а также оптимальное (минимальное) значение линейной функции Z* (на рис. 2.5, б — Z2):

Таким образом, если число независимых уравнений-ограничений, которым должны удовлетворять переменные на два меньше, чем число переменных п (т. е. в ОЗ фигурируют две свободные переменные и любое число базисных), решение ОЗ может быть получено простым геометрическим построением.

Несмотря на то, что это построение относится к частному случаю (т = п- 2), из него вытекают некоторые общие соображения, относящиеся вообще к свойствам решения ОЗ.

1. Решение 03, если оно существует, не может лежать внутри области допустимых решений, а только на ее границе.

2.  Решение 03 может быть и не единственным, если прямая параллельна той стороне многоугольника допустимых решений, где достигается минимум Z, то он достигается не в одной точке, а на всей этой стороне. В этом случае 03 имеет бесчисленное множество оптимальных решений.

3. ОЗ может не иметь решения даже в случае, когда существует ОДР. Это бывает, если ОДР не ограничена.

4.  Решение ОЗ, минимизирующее функцию Z (оптимальное решение), всегда достигается в одной из вершин многоугольника допустимых решений (если оно достигается на целой стороне, то оно же достигается и в каждой из вершин, через которые проходит эта сторона). Решение, лежащее в одной из вершин ОДР, называется опорным решением, а сама вершина — опорной точкой.

5. Для того чтобы найти оптимальное решение, в принципе достаточно перебрать все вершины ОДР (опорные точки) и выбрать из них ту, где функция Z достигает минимума.

6. Если число свободных переменных в ОЗ равно 2, а число базисных — m и решение ОЗ существует, то оно всегда достигается в точке, где по крайней мере две из переменных обращаются в нуль. Действительно, в любой опорной точке пересекаются по крайней мере две из ограничивающих прямых; однако в ней могут пересекаться и более двух (см. рис. 2.5, б).

Случай, когда в оптимальном решении обращаются в нуль не две, а больше переменных, называется вырожденным.

11. Симплексный метод (обязательна его идея, теоремы и симплекс алгоритм).

Решение любой задачи линейного программирования можно найти симплексным методом. Прежде чем применять указанный метод, следует записать исходную задачу в форме основной задачи линейного программирования, если она не имеет такой формы записи.

Симплексный метод решения задачи линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план и каждый ее опорный план является невырожденным). Указанный переход возможен, если известен какой-нибудь исходный опорный план.

Алгоритм симплекс-метода включает следующие этапы:

Составление первого опорного плана. Переход к канонической форме задачи линейного программирования путем введения неотрицательных дополнительных балансовых переменных.

Проверка плана на оптимальность. Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план не оптимальный, и его необходимо улучшить.

Определение ведущих столбца и строки. Из отрицательных коэффициентов индексной строки выбирается наибольший по абсолютной величине. Затем элементы столбца свободных членов симплексной таблицы делит на элементы того же знака ведущего столбца.

Построение нового опорного плана. Переход к новому плану осуществляется в результате пересчета симплексной таблицы методом Жордана—Гаусса.

Теорема 1 Любая точка выпуклого многогранника является выпуклой комбинацией его вершин.

Теорема 2. (Основная теорема линейного программирования) Целевая функция задачи линейного программирования достигает своего экстремума (минимума или максимума) в вершине допустимой области. Если целевая функция достигает экстремального значения более, чем на одной вершине, то она достигает того же значения в любой точке, являющейся выпуклой комбинацией этих вершин.

Теорема 3. Если известно, что система векторов линейно независима и такова, что где все , то точка является вершиной допустимой области.

Теорема 4. Если вершина, то вектора , соответствующие отличным от нуля компонентам , образуют линейно независимую систему.

12. Задачи линейного программирования с искусственной базой (М-задачи). Обязателен алгоритм данной задачи.

13. Двойственность (для задач линейного программирования, основные теоремы двойственности и экономический смысл).

Исходная задача:

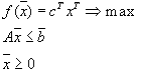
Обычно эта задача связывается с задачей максимизации дохода при производстве некоторой продукции при наличии ограничений на ресурсы. Коэффициенты имеют смысл дохода от единицы продукции j-го ресурса, — количество единиц продукции j-го вида. Коэффициенты имеют смысл затрат i-го ресурса на производство продукции j-го типа. Что же представляет двойственная задача по своему смыслу?

Целевая функция двойственной задачи:,

а ограничения: , где (1) — затраты i-го ресурса на производство единицы продукции j-го типа, а (2) — доход от продажи единицы продукта i-го типа. Поэтому в целевой функции на месте (?)получаем смысл стоимости всех ресурсов, т. е. Задача приобретает смысл: , при ограничениях: , где

• (3) — запасы i-го ресурса;

• (4) — стоимость единицы i-го ресурса;

• (5) — общая стоимость всех ресурсов;

• (6) — запасы i-го ресурса на производство единицы продукции j-го типа;

• (7) — цена единицы i-го ресурса;

• (8) — доход от продажи единицы продукции i-го вида.

Таким образом, задачи симметричной двойственной пары могут быть сформулированы так.

1. Исходная задача. Сколько единиц продукции каждого вида надо выпустить при доходе от продукции единицы j-го типа при имеющихся запасах каждого из ресурсов , чтобы получить максимальный доход?

2. Двойственная задача. Какую цену следует назначить единице каждого из ресурсов , чтобы при заданных величинах дохода от производства единицы каждого вида продукции минимизировать стоимость затрат?

14. Двойственный симплекс метод (алгоритм решения ЗЛП данным методом)

Для реализации двойственного метода необходимо перейти от задачи на минимум к задаче на максимум путем транспонирования матрицы коэффициентов.

Смысл двойственного симплекс-метода заключается в том, что вместо прямой задачи решают двойственную при помощи обычного симплекс-метода. Затем по решению двойственной задачи находят оптимальное решение прямой. Для этого устанавливается взаимнооднозначное соответствие между переменными прямой и двойственной задач. Исходным переменным прямой задачи ставятся в соответствие дополнительные переменные двойственной, а дополнительным переменным исходной задачи ставятся в соответствие исходные переменные задачи прямой.

Пусть решена двойственная задача и получена оптимальная симплекс-таблица. Оптимальное решение прямой задачи определяется коэффициентами F-строки. Переменные прямой задачи приравниваются к коэффициентам при соответствующих им небазисных переменных в F-строке оптимальной симплекс-таблицы двойственной задачи. Остальные переменные равны нулю. Наиболее целесообразно применять двойственный симплекс-метод в случае, когда число ограничений прямой задачи намного больше, чем число неизвестных, а также в задачах целочисленного программирования.

Пример 1. Применяя двойственный симплекс-метод, решить следующую задачу:

F(x)=6x1+12x2 (min)

-2x1+3x2≤6;

4x1-3x2≤12;

3x1+x2≥3;

x1≤2;

x1,2≥0;

Приводим неравенства задачи к знаку ≥, умножая первое, второе и четвертое ограничения на (-1); тогда модель двойственной задачи будет иметь вид:

F(x)=-6y1-12y2+3y3-2y4 (max)

2y1-4y2+3y3-y4≤6

-3y1+3y2+y3≤12

y1≥0, y2≥0, y3≥0, y4≥0.

Решение двойственной задачи осуществляем обычным симплекс-методом (табл. 1 и 2).

Таблица 1

базисные переменные Свободные члены Небазисные переменные

y1 y2 y3 y4

y5 6 2 -4 3 -1

y6 12 -3 3 1 0

F 0 6 12 -3 2

Таблица 2

базисные переменные Свободные члены Небазисные переменные

y1 y2 y5 y4

y3 2 2/3 -4/3 1/3 -1/3

y6 10 -11/3 13/3 -1/3 1/3

F 6 8 8 1 1

Решение, соответствующее табл. 2, является оптимальным. Запишем соответствие между переменными прямой и двойственной задач. Если ограничения прямой задачи приводить к виду равенств, то в качестве дополнительных появятся переменные x3, x4 , x5, x6.

Тогда

В F-строке расположены коэффициенты при небазисных переменных y1, y2, y5, y4. Найдем оптимальное решение прямой задачи:

x3 = 8; x4 = 8; x1 =1; x6 =1.

Переменная x5 , соответствующая y3, и x2, соответствующая y6 , равны нулю.

min F( y) = max F(x) = 6.

Таким образом, решая симплексным методом одну из пары двойственных задач, автоматически получаем решение другой.

15. Специальные задачи линейного программирования (специальные методы решения данных задач).

Специальные задачи линейного программирования :

• Транспортная задача

• Целочисленные задачи линейного программирования

• Задачи параметрического программирования

• Задачи дробно-линейного программирования

• Задачи блочного программирования

• Задачи теории игр и линейное программирование

• Задачи распределения ресурсов

• Задача о смесях

• Задача о назначениях

Задача о назначениях

В общем виде задача о назначениях формулируется следующим образом.

Имеется п работ и п кандидатов для их выполнения. Затраты i -го кандидата на выполнение j -й работы равны c_ij ( ). Каждый кандидат может быть назначен только на одну работу, и каждая работа может быть выполнена только одним кандидатом. Требуется найти назначение кандидатов на работы, при котором суммарные затраты на выполнение работ минимальны.

Запишем формально данную задачу. Пусть х_ij — переменная, значение которой равно 1, если i -й кандидат выполняет j-ю работу, 0 — в противном случае. Тогда условие о том, что каждый кандидат выполняет только одну работу, запишется в виде

Условие о том, что каждая работа может выполняться одним кандидатом, запишется в виде

Целевая функция задачи имеет вид

В функцию входят только те значения c_ij ( , ), для которых x_ij отличны от 0, т. е.. входят затраты, соответствующие назначенным работам.

Математическая модель выглядит следующим образом:

Решить задачу о назначениях – значит найти х_ij, удовлетворяющие (4.14)–(4.16) и доставляющие минимум функции (4.13). Задача

(4.14)–(4.16) является, очевидно, задачей линейного программирования (целевая функция линейна, ограничения линейны) и может быть решена симплекс-методом. Также задача (4.14)–(4.16) – это транспортная задача, в которой правые части ограничений равны 1, а переменные могут принимать только два значения. Однако относительно простая форма задачи позволила разработать для ее решения достаточно простые методы, один из которых – венгерский.

Венгерский метод решения задачи о назначениях

Для решения задачи о назначениях составляют таблицу (табл. 4.8):

Таблица 4.8

№ 1 2 … j ... n

1 c11 c12 ... c1j ... c1n

2 c21 с22 … c2j c2n

... ... ... … ... ... ...

i ci1 ci2 … cij ... cin

… … … … … … …

n cn1 cn2 … cnj … cnn

В левой колонке записаны номера кандидатов, в верхней строке – номера работ. В i-й строке j-м столбце стоят затраты на выполнение i-м кандидатом j -й работы.

В венгерском методе используется следующий принцип: оптимальность решения задачи о назначениях не нарушается при уменьшении (увеличении) элементов строки (столбца) на одну и ту же величину. Решение считается оптимальным, если все измененные образом затраты с'_ij>=0, ( , ) и можно отыскать такой набор х_ij, что

Алгоритм метода содержит следующие шаги.

Шаг 1. Получение нулей в каждой сроке. Для этого в каждой строке определяют наименьший элемент, и его значение отнимают от всех элементов этой строки. Переход к шагу 3.

Шаг 3. Получение нулей в каждом столбце. В преобразованной таблице в каждом столбце определяют минимальный элемент, и его значение вычитают из всех элементов этого столбца. Переход к шагу 3.

Шаг 3. Поиск оптимального решения. Просматривают строку, содержащую наименьшее число нулей. Отмечают один из нулей этой строки и зачеркивают все остальные нули этой строки и того столбца, в котором находится отмеченный нуль. Аналогичные операции последовательно проводят для всех строк. Если назначение, которое получено при всех отмеченных нулях, является полным (т. е. число отмеченных нулей равно п), то решение является оптимальным, в противном случае следует переходить к шагу 4.

Шаг 4. Поиск минимального набора строк и столбцов, содержащих все нули.

Для этого необходимо отметить:

1) все строки, в которых не имеется ни одного отмеченного нуля;

2) все столбцы, содержащие перечеркнутый нуль хотя бы в одной из отмеченных строк;

3)все строки, содержащие отмеченные нули хотя бы в одном из отмеченных столбцов.

Действия 2) и 3) повторяются поочередно до тех пор, пока есть что отмечать. После этого необходимо зачеркнуть каждую непомеченную строку и каждый помеченный столбец.

Цель этого шага – провести минимальное число горизонтальных и вертикальных прямых, пересекающих по крайней мере один раз все нули.

Шаг 5. Перестановка некоторых нулей.

Взять наименьшее число из тех клеток, через которые проведены прямые. Вычесть его из каждого числа, стоящего в невычеркнутых столбцах и прибавить к каждому числу, стоящему в вычеркнутых строках. Эта операция не изменяет оптимального решения, после чего весь цикл расчета повторить, начиная с шага 3.

16. Транспортная задача (Т-задача). Её математическая модель и всё, что связано с её решением. Алгоритмы определения опорного плана. Решение т-задачи методом потенциала.

Транспортная задача. Методы реешния. Потенциалы..

1. Постановка задачи         Классическая транспортная задача ЛП формулируется следующим образом.             Имеется  m  пунктов производства (поставщиков) и n  пунктов потребления (потребителей) однородного продукта. Заданы величины:    - объем производства (запас) i-го поставщика,  i=1, m  ;   - объем потребления   (спрос) j-го потребителя, i=1, n ;    - стоимость перевозки (транспортные затраты) единицы продукта от i-го поставщика к  j-му потребителю.             Требуется составить такой план перевозок, при котором спрос всех потребителей был бы выполнен и при этом общая стоимость всех  перевозок была бы минимальна.              Математическая модель транспортной задачи имеет вид 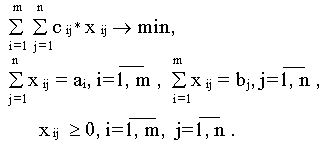                         Транспортная задача, в которой суммарные запасы                                                  и суммарные потребности                                                  совпадают, называется закрытой моделью;  в противном случае - открытой. Открытая модель решается приведением к закрытой.             В случае, когда суммарные запасы превышают суммарные потребности, т.е. 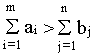                                                 вводится фиктивный n+1 потребитель, потребности которого                                                  В случае, когда суммарные потребности превышают суммарные  запасы,  т.е.                                                 , вводится фиктивный m+1 поставщик, запасы которого 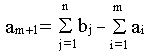                                                 Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика  полагают равными нулю, так как груз в обоих случаях не перевозится.              Прежде чем решать транспортную задачу, необходимо проверить, к какой модели она принадлежит, и если необходимо, то привести ее к закрытой модели.

2 Основные свойство транспортной задачи             Математические модели любых транспортных задач ЛП обладают общими чертами, а именно,             1) коэффициенты  целевой функции неотрицательны (стоимости перевозок не могут быть отрицательными величинами);             2) коэффициенты правых частей ограничений неотрицательны (запасы и потребности продукта);             3) коэффициенты в ограничениях принимают только два значения, это нули и единицы.             В силу этих особенностей транспортная задача обладает следующими свойствами.             Теорема 1.  Базисное решение закрытой модели транспортной задачи содержит m+n-1 базисных компонент.              Доказательство. Количество базисных компонент определяется число линейно-независимых ограничений задачи. В транспортной задаче не все m+n ограничений линейно-независимы.             Действительно, сложив первые m ограничений и  следующие n ограничений задачи, получим 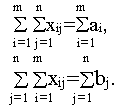                                                Но в закрытой модели выполняется балансовое равенство 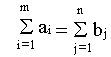                                                поэтому получаем, что нетривиальная линейная комбинация строк ограничений (линейная комбинация с ненулевыми коэффициентами) равна нулю. Это означает, что среди ограничений задачи есть линейно-зависимое ограничение. Следовательно, число линейно-независимых ограничений равно  m+n-1 и базис задачи состоит из m+n-1 компонент. Теорема доказана              В силу специфики содержательной постановки транспортной задачи допустимое решение называется планом, базисное допустимое решение называется опорным планом, оптимальное решение называется оптимальным планом.             Теорема 2.  Оптимальный план закрытой модели транспортной задачи существует всегда.              Доказательство. Оптимальное решение задачи ЛП существует, если, во-первых, существует допустимое решение и, во-вторых, целевая функция ограничена на этом допустимом решении.             Покажем существование допустимого решения. Так как            суммарные запасы                                                     совпадают с суммарными потребностями                                                  то всегда можно найти такой план перевозок, который будет допустимым решением (все запасы вывозятся и все потребности выполняются в силу балансового равенства).              Покажем ограниченность целевой функции.             Так как              следовательно L ограничена снизу нулем для всех допустимых решений.  Теорема доказана  3 Двойственная задача             Запишем транспортную задачу в матричном виде               A- матрица ограничений, имеющая в соответствии с векторами х и b вид :                            Двойственная задача к транспортной задаче в матричном виде будет иметь вид   у- произвольного знака.              Распишем двойственную задачу в скалярном виде. Обозначим компоненты вектора                                      Тогда                          и ограничения двойственной задачи будут иметь вид :                                      или  в общем виде двойственная задача                          Двойственные переменные ai, i=1,...,m, bj, j=1,...,n, называются платежами, а                                      - псевдостоимость перевозок единицы груза из пункта i в пункт j, i=1,...,m, j=1,...,n.  4 Теоремы двойственности             ИЗ теории двойственности ЛП практический интерес представляет вторая теорема двойственности, из которой получается следующий критерий.             Критерий оптимальности транспортной задачи              План перевозок                                     является оптимальным планом тогда и только тогда, когда найдется система платежей                                      для которой выполняются условия :                      Доказательство. Сформулируем вторую теорему двойственности в терминах переменных транспортной задачи.             Ели                          удовлетворяют ограничениям прямой задачи, а                           удовлетворяют ограничениям двойственной задачи, то для оптимальности плана                           необходимо и достаточно выполнение условий                           Условие а) выполняется для любых допустимых решений прямой задачи, так как                                                 Условие b) можно расписать как следствие о дополняющей нежесткости, а именно                          Итак, для базисных переменных                                     имеем равенство                а для небазисных переменных                                       достаточно выполнения допустимости двойственных переменных                                         Таким образом имеем условия 1) и 2) критерия. Критерий доказан.  5 Построение опорного плана транспортной задачи             Методы решения транспортной задачи сводятся к простым операциям с транспортной таблицей, которая имеет вид:                                                               Базисными клетками транспортной таблицы являются клетки с от- личными от нуля положительными перевозками, остальные клетки -  свободные. Базисные клетки образуют опорный план транспортной задачи, если выполняются два условия:             1) сумма перевозок в каждой строке равна запасу   в данной строке;              2) сумма перевозок в каждом столбце равна соответствующему столбцу спросу                                                              Опорный план транспортной задачи содержит не более n+m-1 отличных от нуля перевозок                                                              Опорный план называется вырожденным, если число ненулевых перевозок                                                  меньше и n+m-1, опорный план - невырожден, если число ненулевых перевозок равно n+m-1.              Рассмотрим способы построения опорного плана в невырожденном и вырожденном случаях. 6 Метод   севево-западного угла             Рассмотрим "северо-западный угол" незаполненной таблицы, то есть клетку, соответствующую первому поставщику и первому потребителю.              Возможны три случая.              Это означает, что первый поставщик отгрузил весь произведенный продукт первому потребителю и его  запас равен нулю, поэтому                                      При этом неудовлетворенный спрос в первом пункте потребления равен                                                   то есть спрос первого потребителя полностью удовлетворен и поэтому                     а остаток продукта в первом пункте производства равен                                                   из рассмотрения можно исключить и поставщика, и потребителя. Однако при атом план получается вырожденным,  поэтому условно считается, что выбывает только поставщик,                           а спрос потребителя остается неудовлетворенным и равным нулю.                                                  После этого рассматриваем северо-западный угол оставшейся не- заполненной части таблицы и повторяем те же действия. В результате  через n+m-1   шагов получим опорный план. 7 Пример             Найти опорный план транспортной задачи 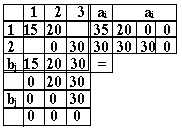                                    В таблице, обведенной двойной чертой , указаны объемы перевозок, полученные методом северо-западного угла. При этом небазисные нулевые перевозки не проставлены. Справа и внизу таблицы содержатся последовательно меняющиеся объемы возможных запасов и спросов. В число базисных вошла нулевая перевозка   , так как на предыдущем шаге                                     и по п.3 метода считается выбывшим только поставщик, а неудовлетворенный спрос второго потребителя равен                                      8 Метод потенциалов             Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией, которая в каждой клетке совершает поворот на 90 , Знаком " + " отмечают те вершины, в которых перевозки увеличиваются, а знаком "- " - те вершины, в которых перевозки уменьшаются. Перемещение какого-то количества единиц груза по циклу означает увеличение перевозок на это количество единиц в положительных вершинах и уменьшение перевозок на это же количество единиц в отрицательных вершинах. При этом, если перевозки остаются неотрицательными, план остается допустимым. Стоимость плана при этом может меняться.             Ценой цикла называется увеличение стоимости перевозок при перемещении единицы груза по этому циклу. Очевидно, цена цикла равна алгебраической сумме стоимостей, стоящих в вершинах цикла, при этом стоимости в положительных вершинах берутся со знаком " +", а стоимости в отрицательных вершинах берутся со знаком " - ".             Идея метода потенциалов состоит в следующем. Для любой свободной клетки транспортной таблицы всегда существует единственный цикл, положительная вершина которого лежит в этой свободной клетке, а все остальные - в базисных. Если цена такого цикла отрицательна, то план можно улучшить перемещением перевозок по данному циклу. Количество единиц груза, которое можно переместить, определяется минимальным значением перевозок, стоящих в отрицательных вершинах цикла (если переместить большее число единиц груза, возникнут отрицательные перевозки). Если циклов с отрицательной ценой нет, то это означает, что дальнейшее улучшение плана невозможно, т.е. оптимальный план найден.             Для нахождения циклов с отрицательной ценой вводится система платежей                                      и определяются величины                                      называемые "псевдостоимостями" перевозок единицы груза из пункта i  в пункт j.  При этом цена цикла пересчета для каждой свободной клетки равна                           если платежи                                                 для всех базисных клеток (i, j)

17. Нелинейное программирование. Классические методы оптимизации. Условие Куна – Таккера для задач не линейного программирования. Условные, безусловные, локальные, глобальные экстремумы.

Нелинейное программирование — случай математического программирования, в котором целевой функцией или ограничением является нелинейная функция.

В отличие от задачи линейного программирования, в задаче программирования нелинейного оптимум не обязательно лежит на границе области, определенной ограничениями.

Методы решения задачи

Одним из методов, которые позволяют свести задачу нелинейного программирования к решению системы уравнений, является метод неопределенных множителей Лагранжа.

Если целевая функция F является линейной, а ограниченным пространством является политоп, то задача является задачей линейного программирования, которая может быть решена с помощью хорошо известных решений линейного программирования.

Если целевая функция является вогнутой (задача максимизации) или выпуклой (задача минимизации) и множеством ограничений служит выпуклая, то задачу называют выпуклой, и в большинстве случаев могут быть использованы общие методы выпуклой оптимизации.

Если целевая функция является отношением вогнутых и выпуклых функций (при максимизации) и ограничения выпуклые, то задача может быть преобразована в задачу выпуклой оптимизации использованием техник дробного программирования.

Существуют несколько методов для решения невыпуклых задач. Один подход заключается в использовании специальных формулировок задач линейного программирования. Другой метод предусматривает использование методов ветвей и границ, где задача делится на подклассы, чтобы быть решенной с выпуклыми (задача минимизации) или линейными аппроксимациями, которые образуют нижнюю границу общей стоимости в пределах раздела. При следующих разделах в определенный момент будет получено фактическое решение, стоимость которого равна лучшей нижней границе, полученной для любого из приближенных решений. Это решение является оптимальным, хотя, возможно, не единственным. Алгоритм можно прекратить на ранней стадии, с уверенностью, что оптимальное решение находится в рамках допустимого отклонения от найденной лучшей точки; такие точки называются ε-оптимальными. Завершение ε-оптимальных точек, как правило, необходимое для обеспечения конечности завершения. Это особенно полезно для больших, сложных задач и задач с неопределенными расходами или значениями, где неопределенность может быть определена из соответствующей оценки надежности.

Дифференцирование и условия регулярности, условия Каруша — Куна — Такера (ККТ) обеспечивают необходимые условия оптимальности решения. При выпуклости, эти условия являются и достаточными.