ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

ИНСТИТУТ КОСМИЧЕСКИХ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Лабораторная работа №2 «Анализ работы классических алгоритмов преследования цели»

Выполнил: Крестьянинов Д. А.

гр. КИ11-14Б

Проверил: Перфильев Д.А.

Красноярск 2012

Тема: Анализ работы классических алгоритмов преследования цели.

Цель: Дать представление о работе классических алгоритмов преследования цели.

Задача: Провести относительный анализ эффективности работы «алгоритмов преследования цели» на примере преследования состояния в задаче «перестановка».

1. Описание задачи.

Основные положения, характеризующие особенности классических алгоритмов преследования:

Алгоритмы преследования цели следует отнести к классу эвристических алгоритмов с явно заданной процедурой планирования.

В состав информации необходимой для работы алгоритмов преследования обычно входят следующие данные:

Vst– вектор скорости цели;

Vss– вектор скорости поисковой системы;

ri– текущие расстояние между ПС и целью (линия визирования);

γ– курсовой угол ПС, (угол между вектором скорости Vssи линией визирования);

φ– курсовой угол цели, (угол между вектором скорости Vstи линией визирования);

η– угол визирования, (угол между линией визирования и направляющими координатной сетки);

ψ– курс ПС (угол между вектором Vssи направляющими координатной сетки).

Классические алгоритмы погони:

1. Алгоритм классической погони

Условия выполнения алгоритма:

1) скорость цели – const ,

2) вид движения цели – прямолинейный;

3) скорость поисковой системы – const ;

4) отношение скоростей – Vst< Vss;

5) курсовой угол ПС, γ= 0, т.е. курс ПС совпадает по направлению с линией визирования. Поэтому, в данном алгоритме преследования η= ψ.

2. Алгоритм с упреждением движения цели

Условия выполнения:

1) Скорость цели – const ,

2) вид движения цели – прямолинейный;

3) скорость поисковой системы – const ;

4) отношение скоростей – Vst< Vss;

5) курсовой угол g в условии погони с постоянным углом упреждения должен быть равен заданной фиксированной величине. При этом должно выполняться условие:

(Vss/ Vst) |sin γ| ≤ 1.

3. Алгоритм параллельного сближения

Условия выполнения:

1) Скорость цели – const ,

2) вид движения цели – прямолинейный;

3) скорость поисковой системы – const ;

4) отношение скоростей – Vst< Vss;

5) курсовой угол ПС: γ = arcsin ( Vstsin φ/ Vss).

4. Алгоритма пропорционального сближения

Условия выполнения:

1) курс ПС: ψ= n ×η, постоянная навигации n;

2) курсовой угол ПС: γ= (n – 1) ×η.

2. Представление пространства поиска.

Поиск представляет собой комплекс действий, выполняемый поисковой системой (ПС) в процессе преследования цели. Комплекс действий включает последовательное выполнение следующих процедур:

1) «генерации» возможных или ограниченных априорной и/или апостериорной информацией о пространстве поиска решений;

2) «проверки» результатов генерации (идентификации полученных решений с целью поиска, их последующие хранение, учет, ранжирование и т.д.);

3) «планирование» способа достижения цели.

Организацию пространства состояний удобно представить в виде ориентированного графа (орграфа), где множество его вершин сопоставимо с состояниями, а множество дуг -сопоставимы с операторами, преобразующими состояния множества.

Представление пространства состояний в виде орграфа позволяет выделить дополнительные свойства и организацию состояний. Свойства определяются отношением подмножеств, входящих и выходящих дуг.

Рассмотрим условия соотношений множеств Yⁱⁿ{y_j} (входящих дуг) и Y^out{y_j} (выходящих дуг), устанавливающие организацию орграфа G: Если для всякой вершины x_iX орграфа G, выполняются условия: Yⁱⁿ{y_j}=n-1 и Y^out{y_j}=n-1, то орграф представляет собой замкнутую структуру.

Пространство поиска в составе пространства состояний образуется за счет обобщения видовых признаков некоторых состояний. В этом случае обобщенные видовые признаки дополняют множество родовых признаков данных состояний, образуя собственное пространство поиска в пространстве состояний или класс состояний.

Каждое состояние пространства состояний получено прямым или обратным преобразованием.

Глубина пространства поиска меньше либо равна n-1, где n-число цифр в состоянии.

Элементы пространства поиска различны.

Между пространством состояний и пространством поиска существуют следующие отношения: 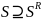и |S | ≥ . Пространство поиска в составе пространства состояний образуется за счёт дальнейшего обобщения видовых признаков некоторых состояний.

В результате обобщенные видовые признаки дополняют множество родовых признаков данных состояний, образуя собственное пространство поиска в пространстве состояний или класс состояний.

Процесс решения задачи в дискретном пространстве может быть представлен как последовательный переход из одной дискретной точки пространства (состояния) в другую. Множество всех дискретных состояний образует дискретное пространство состояний (далее просто пространство состояний): S = {s1, s2, …, sm}, где m  количество всех состояний множества S. Всякое состояние si  S характеризуется множеством признаков K = {k1, k2, …, kn}. Среди множества признаков состояний следует вы-

делить:

1) подмножество родовых признаков состояний KR  K, характери-

зующее всякое состояние пространства состояний. Подмножество родовых

признаков формируется путем выделения тождественных признаков, пред-

ставляющих состояния. Родовые признаки, по сути, выделяют подмноже-

ство состояний из множества состояний, т. е. выполняется условие KR  .

Состояния, принадлежащие подмножеству, составляют уникальное дочер-

нее подпространство состояний;

2) подмножество видовых признаков состояний KV  K выделяет

всякое состояние пространства состояний. Для всякого состояния про-

странства состояний выполняются следующие условия: KV   и KV 

уникально; иначе, будет иметь место такой случай: si  sj  одно со-

стояние.

В качестве примера рассмотрим следующие состояния: s1(ki, kj, ka, kb),

s2(ki, kj, ka, kс), s3(ki, kj, kc, kb) и s4(kd, kf, kg). Отметим, что состояния s1, s2 и s3