15. Численное решение уравнения Пуассона

ПУАССОНА УРАВНЕНИЕ

численные методы решения - методы, заменяющие исходную краевую задачу для уравнения Пуассона ∆u (x) ≡ (1)

системой из Nлинейных алгебраич.

решение к-рой ≡( , позволяет построить нек-рую аппроксимацию Pn Un для решения исходной задачи,N→∞.

В зависимости от способа сравнения решений исходной задачи (1) и дискретной задачи (2) определяются такие важнейшие понятия, как погрешность численного метода и оценка погрешности (точности). Другими характеристиками численных методов служат алгебраич. свойства систем (2) (дискретных аналогов краевых задач), связанные с устойчивостью их решений (корректностью дискретных задач) и возможностью отыскания точных или приближенных решений (2) теми или иными прямыми или итерационными методами при выполнении соответствующей вычислительной работы и соответствующих требованиях на объем используемой памяти ЭВМ (см. Минимизация вычислительной работы).

Важность численного решения краевых задач для П. у. определяется не только тем, что эти задачи часто возникают в разнообразных областях науки и техники, но и тем, что они нередко служат и средством решения более общих краевых задач как для уравнений и систем уравнений эллиптич. типа, так и различных нестационарных систем. Основными численными методами для решения рассматриваемых краевых задач являются проекционные методы и разностные методы.

12. Численное решение обыкновенных дифференциальных уравнений. Метод последовательных приближений Пикара.

Этот метод позволяет получить решение дифференциального уравнения (1) в виде функции, представленной аналитически.

Пусть в условиях теоремы существования требуется найти решение уравнения (1) с начальным условием (2). Проинтегрируем обе части уравнения (1) от x₀ до х :  ,

Очевидно, решение интегрального уравнения (5) будет удовлетворять дифференциальному уравнению (1) и начальному условию (2).

Действительно, при x=x₀получим: . вместе с тем интегральное уравнение (5) позволяет применить метод последовательных приближений. Положим y=y₀ и получим из (5) первое

приближение: . Интеграл в правой части содержит только переменную х; после нахождения этого интеграла будет получено аналитическое выражение приближения y₁(x) как функции переменной х. Заменим теперь в уравнении (5)у найденным значением y₁(x) и получим второе

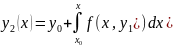
приближение:  и т.д. В общем случае итерационная формула имеет вид:

 (6).

Циклическое применение формулы (6) дает последовательность функций

 (7).

Так как функция f непрерывна в области G, то она ограниченна в некоторой области G  ??? G, содержащей точку (x₀,y₀), то есть

 (8).

Применяя к уравнению (6) в условиях теоремы существования принцип сжимающих отображений, нетрудно показать, что последовательность (7) сходится. Ее предел является решением интегрального уравнения (1) с начальными условиями (2). Это озночает, что k-ый член последовательности (7) является приближением к точному решению уравнения (1) с определенной степенью точности.

Оценка погрешности k-го приближения дается формулой:

 , (9)

Где М - константа Липшица (4), N - верхняя грань модуля функции f из неравенства (8), а величина d для определения окрестности   вычисляется по формуле

 (10)