
- •Часть I теоретические основы информатики
- •Глава 1 информация и общество
- •1.1 Развитие информационного общества
- •1.2 Основные понятия и определения
- •1.3 Информатика и ее задачи
- •Глава 2 информация
- •2.1 Понятие информации
- •2.2 Информационные сигналы
- •2.3 Преобразование сообщений
- •2.4 Понятие данных
- •2.5 Свойства информации
- •2.6 Меры информации
- •2.7 Экономическая информация
- •Глава 3 представление информации
- •3.1 Понятие о формальном языке
- •3.2 Язык чисел (системы счисления)
- •3.3 Язык логики
- •1. Аксиомы алгебры логики
- •2. Свойства дизъюнкции и конъюнкции
- •3. Законы алгебры логики
- •Глава 4 информационные процессы
- •4.1 Хранение данных
- •4.2 Обработка данных (кодирование)
- •4.3 Передача данных
- •Глава 5 эвм — техническое средство информатики
- •5.1 Понятие об эвм
- •5.2 Архитектура персонального компьютера
- •5.3 Представление данных в компьютере
- •5.4 Программное обеспечение компьютера
- •Московская государственная академия приборостроения и информатики
- •1 07996, Москва, ул. Стромынка, 20
1. Аксиомы алгебры логики
а. ![]() —
отрицание отрицания;
—
отрицание отрицания;
б. ![]() ,
,
![]() —
правила подобных преобразований;
—
правила подобных преобразований;
в. ![]() ;
;
г. ![]() ;
;
д. ![]() ;
;
е. ![]() ;
;
ж. ![]() ;
;
з. ![]() .
.
2. Свойства дизъюнкции и конъюнкции
а. Свойство ассоциативности (сочетательный закон):
![]() ,
,
![]() .
.
б. Свойство коммутативности (переместительный закон):
![]() ,
,
![]() .
.
в. Свойство дистрибутивности (распределительный закон):
![]() .
.
3. Законы алгебры логики
а. Законы поглощения:
![]() ,
,
![]() .
.
б. Законы двойственности для сложения и умножения (законы де Моргана):
![]() ,
,
![]() .
.
Совершенные нормальные формы (СНФ)
Пусть
![]() и
и
![]() —
некоторые высказывания. Тогда можно
образовать сложные высказывания
ИЛИ
,
И
,
НЕ
,
введя операции дизъюнкции (ИЛИ),
конъюнкции (И) и отрицания (НЕ).
—
некоторые высказывания. Тогда можно
образовать сложные высказывания
ИЛИ
,
И
,
НЕ
,
введя операции дизъюнкции (ИЛИ),
конъюнкции (И) и отрицания (НЕ).
Электронные схемы, реализующие эти операции, называют логическими элементами. На основе логических элементов строятся более сложные узлы и агрегаты, работа которых может быть описана посредством алгебры логики, т. е. с помощью переключательных (булевых) функций.
В самом общем случае сколь угодно сложная логическая функция может быть представлена в виде:
![]() ,
,
где ![]() —
логические переменные, принимающие
значения 0 или 1.
—
логические переменные, принимающие
значения 0 или 1.
Логические переменные могут быть действительными и фиктивными.
Переменная действительна, если значение функции, куда она входит, изменяется при изменении значения этой переменной. В противном случае она фиктивна.
Логические функции многих переменных могут задаваться таблично. Рассмотрим пример табличного определение функции трех переменных (табл. 6)
Табл. 6 Пример табличного задания логической функции трех переменных
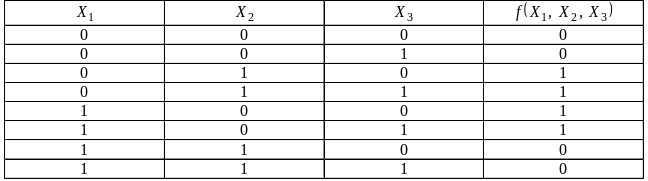
Из
таблицы видно, что переменные
![]() и
и
![]() —
действительные, а переменная
—
действительные, а переменная
![]() —
фиктивная, т. к. справедливо соотношение
—
фиктивная, т. к. справедливо соотношение
![]() ,
при любых комбинациях
и
.
Переменную
можно сократить из выражения булевой
функции. Следовательно, для функций
алгебры логики существует возможность
сокращать (расширять) количество
переменных устранением (введением)
фиктивных.
,
при любых комбинациях
и
.
Переменную
можно сократить из выражения булевой
функции. Следовательно, для функций
алгебры логики существует возможность
сокращать (расширять) количество
переменных устранением (введением)
фиктивных.
Булевы функции могут задаваться аналитически, т. е. в виде формул. При этом сложные логические функции можно выражать через более простые логические функции.
Минимальный набор простых логических функций, посредством которого может быть представлена любая функция алгебры логики (ФАЛ), называется логическим базисом или полной системой.
Базис минимален, если удаление хотя бы одной функции превращает систему ФАЛ в неполную. Примеры базисной системы функций: (И, НЕ); (ИЛИ, НЕ). На практике намного удобней использовать не минимальный базис. И, ИЛИ, НЕ.
Любая таблично заданная логическая функция может выражаться через набор конъюнктивных и дизъюнктивных термов или импликант:
![]() ,
,
где ![]() —
конъюнктивный терм;
—
конъюнктивный терм;
![]() —
дизъюнктивный терм.
—
дизъюнктивный терм.
Конъюнктивный терм — это логическое произведение переменных и их отрицаний.
Дизъюнктивный терм — это логическая сумма переменных и их отрицаний.
Если терм ФАЛ содержит полный набор переменных, связанных операцией конъюнкции, он носит название минтерм (конституента 1).
Термы ФАЛ, состоящие из полного набора переменных, связанных операциями дизъюнкции, называются макстермами (конституенты 0).
Представление ФАЛ в аналитическом виде возможно в дизъюнктивной нормальной форме и в конъюнктивной нормальной форме.
Дизъюнктивная нормальная форма (ДНФ) — это сумма конъюнктивных термов (ДНФ не содержит скобок).
Конъюнктивная нормальная форма (КНФ) — это произведение дизъюнкивных термов.
Всякая сложная логическая функция может быть сведена к различным ДНФ или КНФ. Однозначное соответствие между функцией алгебры логики и ее представлением в дизъюнктивной или конъюнктивной нормальной форме обеспечивается только в одном случае — когда все конъюнкции ДНФ (термы) составлены из полного числа переменных или когда каждая дизъюнкция КНФ содержит максимальное число переменных.
ДНФ и КНФ, состоящие только из минтерм и макстерм носят названия совершенной дизъюнктивной нормальной формы (СДНФ) и, соответственно, совершенной конъюнктивной нормальной формы (СКНФ).
Алгоритм получения СДНФ из таблицы истинности, задающей функцию:
1. Выбрать из таблицы
набор переменных
![]() для которого справедливо соотношение
для которого справедливо соотношение
![]() .
.
2. Сформировать из этого набора переменных и их отрицаний минтерм, т. е. произведение переменных или их отрицаний: если переменная набора имеет нулевое значение, то она берется с отрицанием; переменные, имеющие единичные значения в данном наборе не инвертируются.
3. Повторить пункты 1 и 2 для всех других наборов таблицы, где логическая функция равна 1.
4. Построить СДНФ путем логического суммирования полученных минтермов.
Аналогично определяется алгоритм для получения СКНФ:
1. Выбрать из таблицы
набор переменных
для которого справедливо соотношение
![]() .
.
2. Сформировать макстерм, т. е. дизъюнктивный набор переменных и их отрицаний: если переменная данного набора равна 0, то она включается в сумму без отрицания, а при равенстве 1 она инвертируется.
3. Повторить пункты 1 и 2 для всех наборов переменных, где значение функции равно 0.
4. Построить СКНФ из полученных дизъюнкций переменных и их отрицаний путем логического умножения.

Упрощение логических функций
Совершенные нормальные формы однозначно представляют ФАЛ. Если условие однозначности не является необходимым, то во многих случаях СНФ имеют некоторую избыточность, т. е. включают фиктивные переменные, от которых необходимо избавиться до аппаратной реализации ФАЛ. Минимальная форма представления ФАЛ содержит минимальное количество термов и переменных в термах и более не допускает никаких упрощений (минимизации). Так при минимизации СДНФ сокращается до минимума количество конъюнкций и число переменных в каждой из них.
Минимизация (упрощение) булевых функций производится с помощью теорем алгебры логики и может быть реализована аналитическими, графическими и арифметическими методами с помощью теоремы Квайна Мак-Класки.
Наиболее
эффективными приемами аналитических
методов минимизации являются вынесение
за скобки общих членов, а также применение
двойного отрицания, теоремы де-Моргана,
законов поглощения и склеивания. При
этом, наряду с полным склеиванием, т. е.
использованием зависимости
![]() или
или
![]() (склеивание по
)
часто применяют неполное склеивание —
оба члена склеивания или один из них
остаются и склеиваются с другими членами
СДНФ. Неполное склеивание может
рассматриваться как сочетание закона
склеивания и идемпотентности. При
преобразовании следует помнить, что
логические операции имеют старшинство —
в порядке убывания
(склеивание по
)
часто применяют неполное склеивание —
оба члена склеивания или один из них
остаются и склеиваются с другими членами
СДНФ. Неполное склеивание может
рассматриваться как сочетание закона
склеивания и идемпотентности. При
преобразовании следует помнить, что
логические операции имеют старшинство —
в порядке убывания
![]() .
.
Пример: Упростить выражение
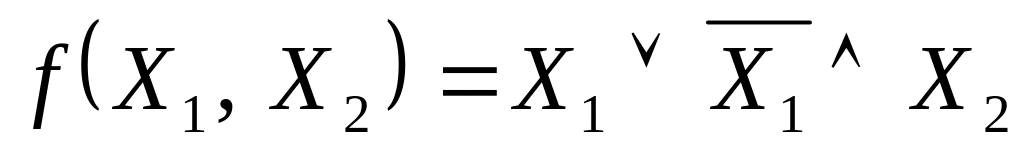 .
.
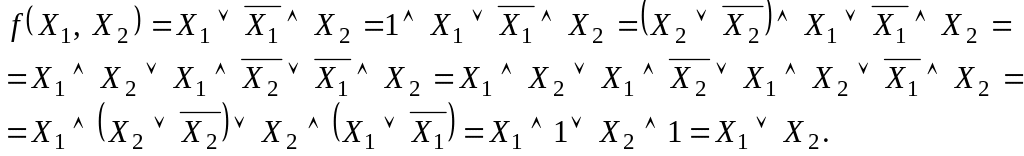


Чтобы проверить правильность достаточно вместо переменных в полученную функцию подставить их значения из таблицы.
Построение логических схем
Электронные схемы можно условно разбить на два вида:
– схемы первого рода — комбинационные схемы;
– схемы второго рода — накапливающие схемы (элементы с памятью).
Комбинационные схемы — схемы, выходной сигнал в которых зависит только от состояния входов (наличия входных сигналов) в каждый момент времени.
Накапливающие схемы — схемы, выходной сигнал в которых зависит как от входных сигналов, так и от состояния схемы в предыдущие моменты времени.
Большинство ЭВМ состоит из комбинации схем первого и второго родов разной сложности.
Схемы различают в зависимости от количества входов и выходов.
Для построения логических комбинационных схем используются специальные графические изображения логических функций.
Задача синтеза электронной логической схемы формулируется следующим образом: при заданных входных переменных и известной выходной функции необходимо синтезировать логическое устройство, выполняющее эту функцию. При этом обычно налагаются ограничения на используемую систему логических элементов (логический базис). В результате решения задачи синтеза возникает логическая схема, воспроизводящая заданную функцию.
На практике используют схемы простейших логических функций (рис. 18) таких как элемент НЕ (инвертор), элемент ИЛИ (дизъюнктор), элемент И (коньюнктор), элемент ИЛИ-НЕ (дизъюнктор/инвертор), элемент И-НЕ (коньюнктор/инвертор).

Рис. 18 Обозначения логических функций на электронных схемах
При решении задачи анализа и синтеза используют полные базисы функций. При этом каждую логическую функцию, входящую в базис, сопоставляют с некоторым физическим элементом, следовательно, логическую схему можно заменить структурной схемой, состоящей из физических элементов. Этот путь позволяет соединить математическую задачу синтеза логической схемы с инженерной задачей проектирования электронной схемы. При разработке электронной схемы за основные критерии принимают: минимум аппаратуры, минимум типов применяемых элементов, максимум надежности.
С позиций математической логики задача синтеза решается при обеспечении минимального числа логических операторов, минимального количества типов логических операторов. Сформулируем последовательные этапы решения задачи синтеза логической схемы:
1. Составление математической модели (системы логических уравнений), отображающие происходящие в схеме процессы.
2. Анализ логических уравнений и получение минимальной формы для каждой из них в заданном базисе.
3. Переход от логических уравнений к логической (структурной) схеме посредством применения логических операторов. (Логический оператор схемы — элементарная логическая функция, с помощью которой описывается работа схемы).
В общем случае задача синтеза имеет множество решений, которые зависят от выбранной системы логических элементов. Если за критерий оптимальности схемы взять минимальное количество логических связок, то это потребует нахождения минимальной формы для функции алгебры логики. В случае сложных схем, имеющих несколько выходов, можно решить задачу синтеза путем декомпозиции частных схем с одним выходом.
Кроме комбинационных схем, называемых схемами первого рода, различают, как упоминалось выше, накапливающие схемы, включающие элементы с памятью. Основной особенностью схем с памятью является тот факт, что алгоритм их работы зависит от времени. Поэтому в число переменных для функций, описывающих накапливающие схемы, должно входить время ( ). Однако время не является двоичной переменной. Поэтому вводится так называемое автоматное время, принимающее дискретные целочисленные значения . Это означает, что работа схемы с памятью распадается на ряд интервалов, в течение которых автоматное время условно принимает постоянное значение.
Временная булева функция (ВБФ) это логическая функция
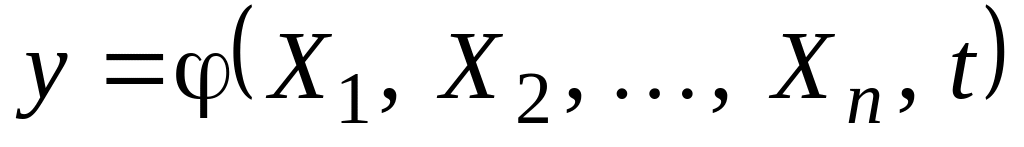 ,
принимающая значение
,
принимающая значение
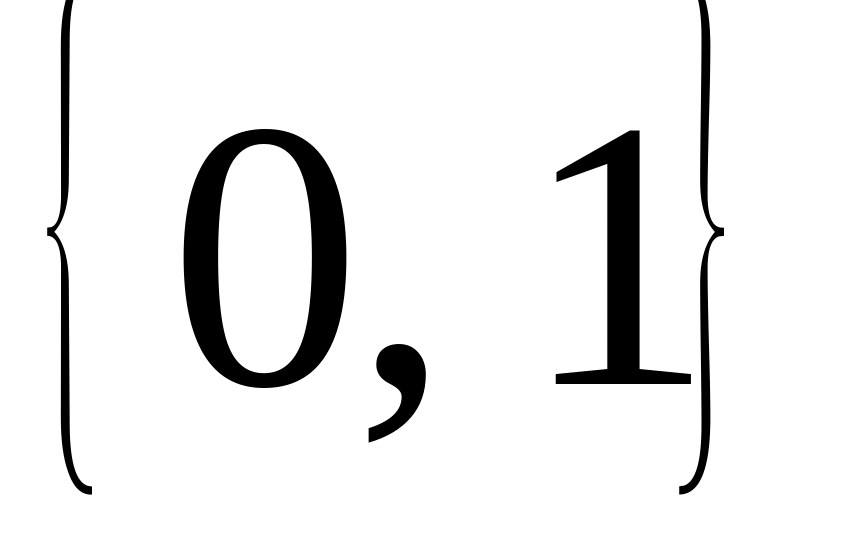 при
при
 ,
где
,
где
 —
количество интервалов автоматного
времени.
—
количество интервалов автоматного
времени.
Существует теорема о том, что любая периодическая временная булева функция может быть представлена в аналитическом виде следующим образом:
![]() ,
,
где
![]() —
конъюнктивный терм (или их дизъюнкция)
от переменных
;
—
конъюнктивный терм (или их дизъюнкция)
от переменных
;
![]() —
вспомогательная функция, принимающая
значение 1 в момент времени
—
вспомогательная функция, принимающая
значение 1 в момент времени
![]() и 0 во всех других случаях.
и 0 во всех других случаях.
Такая форма представления временных логических функций позволяет применить к функциям » все методы упрощения и минимизации ФАЛ.

Схема
для полученной формулы строится
аналогично построению комбинационных
схем с элементом дешифратором (рис. 19).
Выход
—
выход
-й
функции, принимающей значение, равное
1 в момент времени
,
а все остальные
![]() в данный момент равны 0.
в данный момент равны 0.
Если ВБФ зависит еще и от своих предшествующих значений, то она называется рекуррентной булевой функцией (РБФ).
Аналитически РБФ записывается в виде:
![]() ,
,
где ![]() —
текущее значение
‑й
переменной;
—
текущее значение
‑й
переменной;
![]() —
значение функции в момент времени
—
значение функции в момент времени
![]() .
.
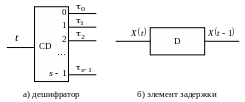
Рис. 19 Изображение дешифратора и элемента задержки на электронных схемах
Если,
например, для функции
справедливо соотношение
![]() ,
то это означает, что значение выходного
сигнала схемы в момент времени
,
то это означает, что значение выходного
сигнала схемы в момент времени
![]() равен значению входного сигнала в момент
времени
.
Таким образом, схема выдает значение
входа с задержкой на один интервал
времени. Если такое соотношение
справедливо для всех моментов времени,
на которых определена функция
,
то соответствующая ей схема называется
элементом (схемой) задержки. Логический
оператор, соответствующий элементу
задержки представлен на рис. 19.
равен значению входного сигнала в момент
времени
.
Таким образом, схема выдает значение
входа с задержкой на один интервал
времени. Если такое соотношение
справедливо для всех моментов времени,
на которых определена функция
,
то соответствующая ей схема называется
элементом (схемой) задержки. Логический
оператор, соответствующий элементу
задержки представлен на рис. 19.
Любая РБФ может быть реализована с помощью набора логических операторов, представляющих обычные функции алгебры логики и операторов схем задержки.
