3.3 Язык логики

Логика — наука, изучающая методы установления истинности или ложности одних высказываний на основе истинности или ложности других высказываний. В математической логике содержание рассуждений отбрасывается, а используется только их форма и логическое значение. Основой внутреннего языка базового технического средства информатики — компьютера является язык логики, называемый еще булевой алгеброй. Булева алгебра чрезвычайно важна в проектировании аппаратных средств ЭВМ, в разработке языков программирования и в конструировании дискретных устройств автоматики.

Логические функции

В 17 веке немецкий ученый Лейбниц задумал создать новую науку, в которой каждому высказыванию соответствовал бы свой символ, а рассуждения имели бы вид вычислений. Эта идея была воплощена в жизнь в 19 веке ирландским математиком Джорджем Булем, который заложил основы алгебры логики, схожей с обычной алгеброй, но вместо чисел буквами обозначаются высказывания. На языке алгебры логики можно описать рассуждения и получить («вычислить») результаты. Однако данной алгеброй охватываются не все рассуждения, а только определенный их тип.

Основными понятиями в математической логике являются логическое высказывание, высказывательные формы, предикаты и кванторы.

• Высказыванием (суждением) называется повествовательное и утвердительное предложение, о котором можно сказать в данный момент, что оно истинно или ложно, но не то и другое одновременно.

Высказывание истинно, если оно отражает действительное положение вещей и ложно, если оно противоречит действительности. Обозначаются высказывания буквами латинского алфавита , , и т. д. Истинность высказывания выражается через логические величины, принимающие значения «True» (истина) или «False» (ложь) и обозначаемых, соответственно, цифрой 1 — «True», а цифрой 0 — «False».

Логическая величина может быть логической переменной или логической константой.

Над логическими переменными или константами определены логические операции, посредством которых могут строиться сложные логические выражения.

• Высказывательной (пропозициональной) формой называется предложение, содержащее хотя бы одну переменную и становящееся высказыванием при подстановке хотя бы одного значения этой переменной.

Из математики известно, что функция определена, если задано:

1. Область определения функции, т. е. некоторое множество возможных значений аргумента.

2. Область значений функции, т. е. множество возможных значений функции.

3. Правило соответствия, согласно которому каждому значению аргумента из области определения ставится в соответствие значение функции — ,  — функция,  — аргумент,  — правило соответствия.

• Функция одной или нескольких переменных, область определения которой задана множеством , а область значений описывается множеством называется предикатом.

• Предикат, аргументы которого могут принимать только значения 0 или 1 (определены на множестве ) называется булевой функцией.

Таким образом, булевой или переключательной функцией называется функция, принимающая только значения 0 или 1 и аргументы которой также могут принимать только значения 0 или 1.

Булевы функции могут быть заданы специальными таблицами истинности или аналитически в виде специальных высказывательных форм, называемых булевыми формами с использованием логических операций.

В математике операциями называют такие функции, области значений которых совпадают с областями определения их аргументов (бинарные операции сложения, вычитания, умножения, деления и унарная операция изменения знака).

Логическая операция НЕ

В математической логике также имеются несколько бинарных операций и одна унарная — отрицание: операция НЕ (логическое отрицание, инверсия). Отрицанием высказывания называется операция, результат которой истинен, когда ложно, и ложен, когда истинно. Отрицание обозначается: (которое читается: есть инверсия от ). Таблица истинности, отражающая ее значения при всевозможных комбинациях логических переменных, в нее входящих, представлена в табл. 3. Графическая иллюстрация операции НЕ представлена в виде диаграммы Венна (рис. 12).

Т абл. 3 Таблица истинности логической операции НЕ

Электронная схема, реализующая операцию отрицания, называется инвертором или схемой НЕ. Ее условное графическое изображение представлено на рис. 13. На выходе элемента НЕ появляется сигнал при его отсутствии на входе.

Рис. 13 Изображение операции НЕ на электронных схемах

Логическая операция ИЛИ

Операция ИЛИ (логическое сложение, дизъюнкция). Это логическая операция над двумя переменными ( и ), результат которой истинен, если хотя бы одна из составляющих его переменных истинна. Операция ИЛИ обозначается символом « », который соответствует союзу «или»; знаком «+», обозначающим логическое сложение:

или .

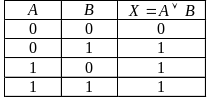
Таблица истинности, отражающая ее значения, и диаграмма Венна представлены в табл. 4 и на рис. 14 соответсвенно.

Т абл. 4 Таблица истинности логической операции ИЛИ

Электронная схема, реализующая операцию ИЛИ, называется логической схемой ИЛИ, дизъюнктором или разделительной схемой. Ее условное графическое изображение представлено на рис. 15. На выходе элемента ИЛИ сигнал соответствующий 1 появляется в том случае, если есть сигнал 1 хотя бы одном из его входов.

Рис. 15 Изображение операции ИЛИ в электронных схемах

Следует отметить, что операция ИЛИ справедлива для любого числа логических переменных.

Логическая операция И

Операция И (логическое умножение, конъюнкция). Это логическая операция над двумя переменными ( и ), результат которой истинен, если истинны значения обеих переменных. Операция И обозначается символом « », который соответствует союзу «и» или знаком умножения « », обозначающим логическое умножение:

или .

Таблица истинности, отражающая ее значения, и диаграмма Венна представлены в табл. 5 и на рис. 16 соответсвенно.

Т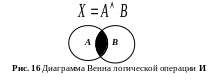 абл. 5 Таблица истинности логической операции И

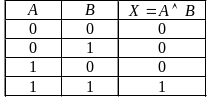
Электронная схема, реализующая операцию И, называется логической схемой И, конъюнктором или схемой совпадения. Условное графическое обозначение элемента И представлено на рис. 17. На выходе элемента И сигнал, соответствующий 1, появляется только в том случае, если есть сигналы на всех его входах.

Рис. 17 Изображение операции И в электронных схемах

Операция И справедлива для любого числа логических переменных.

Элементарные функции алгебры логики находятся в определенной связи друг с другом, что отражается на уровне аксиом, свойств и законов.