
- •1. Законы ома и кирхгофа и их использование для расчетов цепей постоянного тока.
- •2. Режимы работы электрических цепей.
- •3. Расчет цепей постоянного тока с одним источником тока.
- •4. Расчет сложных цепей постоянного тока с применением различных методов.
- •5. Законы фарадея-максвелла и их использование для объяснения работы различных электромагнитных аппаратов.
- •7. Получение синусоидального тока. Синхронные генераторы.
- •8. Значения величин переменного тока, векторные диаграммы.
- •9. Сопротивления и мощности в цепях переменного тока. Треугольники
- •10. Цепи переменного тока с единичными элементами r, l, c.
- •11. Цепь переменного тока с последовательным соединением элементов
- •12. Цепи переменного тока со смешанным соединением элементов r, l, c.
- •13. Символический метод расчета цепей переменного тока.
- •15. Четырехпроводная трехфазная система. Векторная диаграмма. Роль нулевого провода.
- •16. Трансформаторы. Устройство, принцип действия, режимы работы
- •17. Опыты холостого хода и короткого замыкания трансформатора.
- •18. Внешняя характеристика и кпд трансформатора. Трехфазные трансформаторы.
- •19. Асинхронные двигатели. Устройство, принцип действия, режимы работы.
- •20. Рабочие характеристики и способы пуска Асинхронного Двигателя.
- •21. Синхронные двигатели. Устройство, принцип действия и назначение.
- •22. Характеристики синхронных двигателей и электрические схемы их включения.
- •Устройство электрической машины постоянного тока
- •Устройство электрической машины постоянного тока
10. Цепи переменного тока с единичными элементами r, l, c.
Резистивным
элементом
(резистором) (графическое изображение на
рис. 13) называется математическая модель
любого электротехнического устройства
(или его части) в котором энергия
электромагнитного поля преобразуется
в теплоту.
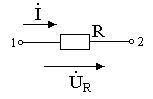 Рис.
13.
Соотношение между током, протекающим
через резистор, и падением напряжения
на его выводах определяется законом
Ома.
Рис.
13.
Соотношение между током, протекающим
через резистор, и падением напряжения
на его выводах определяется законом
Ома.
![]() .
Параметр,
характеризующий резистивный элемент
(R) называется сопротивлением электрическому
току. Измеряется в Омах (Ом, или
.
Параметр,
характеризующий резистивный элемент
(R) называется сопротивлением электрическому
току. Измеряется в Омах (Ом, или
![]() ).
Величина
обратная сопротивлению называется
проводимостью электрической ветви и
обозначается буквой g. Измеряется
проводимость в Сименсах (См, Ом-1).
).
Величина
обратная сопротивлению называется
проводимостью электрической ветви и
обозначается буквой g. Измеряется
проводимость в Сименсах (См, Ом-1).
![]() .
Если
принять, что ток, протекающий по
сопротивлению равен
.
Если
принять, что ток, протекающий по
сопротивлению равен
![]() ,
то падение напряжения на сопротивлении
будет определяться как:
,
то падение напряжения на сопротивлении
будет определяться как:
![]() .
Воспользовавшись
временной формой записи для тока и
напряжения на резисторе, перейдем к
показательной форме для действующих
значений. (См. § 1.2).
.
Воспользовавшись
временной формой записи для тока и
напряжения на резисторе, перейдем к
показательной форме для действующих
значений. (См. § 1.2).
![]() ,
и
,
и
![]() .
На
рис. 14 представлены векторы тока
.
На
рис. 14 представлены векторы тока
![]() и
напряжения
и
напряжения
![]() на
комплексной плоскости.
на
комплексной плоскости.
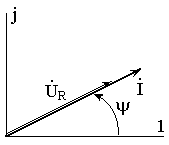 Рис.
14.
Из сказанного видно, что вектор
напряжения на резистивном элементе
совпадает по фазе с вектором тока,
протекающим через резистор, т.е. эти
векторы синфазные.
Рис.
14.
Из сказанного видно, что вектор
напряжения на резистивном элементе
совпадает по фазе с вектором тока,
протекающим через резистор, т.е. эти
векторы синфазные.
Индуктивным
элементом
(катушкой индуктивности) называется
математическая модель любого
электротехнического устройства (или
его части) способного накапливать
энергию магнитного поля в локализованном
объёме. Графическое изображение
индуктивного элемента показано на рис.
15 а.
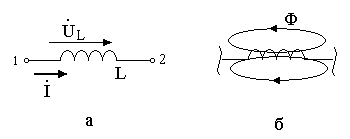 Рис.
15.
Если по катушке индуктивности
протекает ток, то вокруг витков катушки
возникает магнитный поток Ф
(рис. 15 б).
Обозначим число витков катушки как W,
тогда магнитный поток взаимодействующий
(“сцепленный”) с витками будет называться
потокосцеплением ψ и определяться
формулой:
Рис.
15.
Если по катушке индуктивности
протекает ток, то вокруг витков катушки
возникает магнитный поток Ф
(рис. 15 б).
Обозначим число витков катушки как W,
тогда магнитный поток взаимодействующий
(“сцепленный”) с витками будет называться
потокосцеплением ψ и определяться
формулой:
![]() .
Из
курса физики известно определение
индуктивности, как параметра связи
между величиной потокосцепления
самоиндукции
.
Из
курса физики известно определение
индуктивности, как параметра связи
между величиной потокосцепления
самоиндукции
![]() и
током I,
протекающим по катушке:
и
током I,
протекающим по катушке:
![]() Гн.
Связь
между током, протекающим по катушке
индуктивности, и падением напряжения
на её выводах вытекает из закона
электромагнитной индукции:
Гн.
Связь
между током, протекающим по катушке
индуктивности, и падением напряжения
на её выводах вытекает из закона
электромагнитной индукции:
![]() .
С
учётом того, что
.
С
учётом того, что
![]() ,
а
,
а
![]() уравнение
можно записать:
уравнение
можно записать:
![]() ;
Допустим,
что ток изменяется по синусоидальному
закону:
Тогда
выражение для UL
можно записать как
;
Допустим,
что ток изменяется по синусоидальному
закону:
Тогда
выражение для UL
можно записать как
![]() .
Воспользовавшись
формулами приведения запишем:
.
Воспользовавшись
формулами приведения запишем:
![]() .
Если
перейти из временной области к изображению
на комплексной плоскости, то можно
записать для действующих значений
выражения тока и напряжения на индуктивном
элементе:
.
Если
перейти из временной области к изображению
на комплексной плоскости, то можно
записать для действующих значений
выражения тока и напряжения на индуктивном
элементе:
![]() ;
;
![]() ;
Из
формулы Эйлера следует, что
;
Из
формулы Эйлера следует, что
![]() тогда
выражение для напряжения на катушке
индуктивности можно записать:
тогда
выражение для напряжения на катушке
индуктивности можно записать:
![]() ;
Эта
формула называется законом Ома в
дифференциальной форме записи, а
коэффициент
;
Эта
формула называется законом Ома в
дифференциальной форме записи, а
коэффициент
![]() называется
индуктивным сопротивлением (ХL)
и измеряется в Омах. Величина
ХL,
является реактивным параметром и
принадлежит оси мнимых чисел на
комплексной плоскости. Поэтому справедлива
запись:
называется
индуктивным сопротивлением (ХL)
и измеряется в Омах. Величина
ХL,
является реактивным параметром и
принадлежит оси мнимых чисел на
комплексной плоскости. Поэтому справедлива
запись:
![]() (OM);
Величина
обратная индуктивному сопротивлению
называется индуктивной проводимостью
BL
и измеряется в Сименсах:
(OM);
Величина
обратная индуктивному сопротивлению
называется индуктивной проводимостью
BL
и измеряется в Сименсах:
![]() (См).
На
рис. 16 представлены векторы тока
(См).
На
рис. 16 представлены векторы тока
![]() и
напряжения
и
напряжения
![]() на
комплексной плоскости.
на
комплексной плоскости.
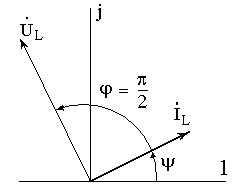 Рис.
16.
Угол между током и напряжением в
электротехнике называется углом
Рис.
16.
Угол между током и напряжением в
электротехнике называется углом
![]() и
является одним из основных энергетических
показателей электрической системы. В
данном случае
и
является одним из основных энергетических
показателей электрической системы. В
данном случае
![]() .
.
Емкостным
элементом
(конденсатором) называется математическая
модель любого электротехнического
устройства (или его части) способного
накапливать энергию электрического
поля в локализованном объёме. Графическое
изображение ёмкостного элемента показано
на рис.17 а.
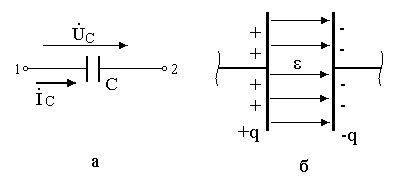 Рис.
17.
Если к конденсатору приложить
напряжение, то на обкладках появится
заряд q.
На одной обкладке – положительный, а
на другой – отрицательный и внутри
конденсатора будет создано электрическое
поле с напряженностью
Рис.
17.
Если к конденсатору приложить
напряжение, то на обкладках появится
заряд q.
На одной обкладке – положительный, а
на другой – отрицательный и внутри
конденсатора будет создано электрическое
поле с напряженностью
![]() .
Из
курса физики известно определение
емкости как параметра связи между
зарядом тел и напряжением между этими
телами:
.
Из
курса физики известно определение
емкости как параметра связи между
зарядом тел и напряжением между этими
телами:
![]() (Ф).
Пусть
напряжение, приложенное к конденсатору,
изменяется по синусоидальному закону:
(Ф).
Пусть
напряжение, приложенное к конденсатору,
изменяется по синусоидальному закону:
![]() .
Тогда, чтобы определить ток необходимо
вспомнить его определение. Электрический
ток это направленное движение зарядов,
а величина электрического тока
характеризуется количеством зарядов
прошедших через единицу сечения
проводника за единицу времени, или:
.
Тогда, чтобы определить ток необходимо
вспомнить его определение. Электрический
ток это направленное движение зарядов,
а величина электрического тока
характеризуется количеством зарядов
прошедших через единицу сечения
проводника за единицу времени, или:
![]() .
Примем,
что
.
Примем,
что
![]() и
определим ток через емкость:
и
определим ток через емкость:
![]() .
Воспользовавшись
формулами приведения запишем:
.
Воспользовавшись
формулами приведения запишем:
![]() .
Если
перейти из временной области к изображению
на комплексной плоскости, то можно
записать для действующих значений
выражения тока и напряжения на емкостном
элементе:
.
Если
перейти из временной области к изображению
на комплексной плоскости, то можно
записать для действующих значений
выражения тока и напряжения на емкостном
элементе:
![]() ;
;
![]() ;
Из
формулы Эйлера следует, что
тогда
выражение для тока через емкость можно
записать:
;
Из
формулы Эйлера следует, что
тогда
выражение для тока через емкость можно
записать:
![]() Величина
Величина
![]() называется
емкостной проводимостью и обозначается
BС.
Емкостная проводимость реактивный
параметр, поэтому справедлива запись:
называется
емкостной проводимостью и обозначается
BС.
Емкостная проводимость реактивный
параметр, поэтому справедлива запись:
![]() .
Величина
обратная проводимости называется
сопротивлением, исходя из этого, запишем
для емкостного сопротивления:
.
Величина
обратная проводимости называется
сопротивлением, исходя из этого, запишем
для емкостного сопротивления:
![]() .
Модуль
емкостного сопротивления будет равен:
.
Модуль
емкостного сопротивления будет равен:
![]() На
рис. 18 представлены векторы тока
На
рис. 18 представлены векторы тока
![]() и
напряжения
и
напряжения
![]() на
комплексной плоскости.
на
комплексной плоскости.
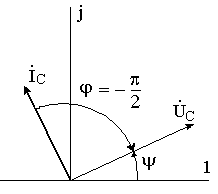 Рис.
18.
Угол между током и напряжением в
данном случае отрицательный:
Рис.
18.
Угол между током и напряжением в
данном случае отрицательный:
![]() .
.
