1. Постановка задачи лин. Программирования. Целевая ф-я. Множество доп. Планов. Оптим. План.

Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений. Классические же методы дифференциального исчисления связаны с нахождением экстремумов функции во внутренней точке области допустимых значений. Отсюда — необходимость разработки новых методов. В общем виде задача линейного программирования ставится следующим образом.

Общей задачей линейного программирования называют задачу

(2.1)

при ограничениях

(2.2)

(2.3)

  (2.4)

(2.5)

- произвольные (2.6)

где - заданные действительные числа; (2.1) – целевая функция; (2.1) – (2.6) –ограничения; - план задачи.

Пусть ЗЛП представлена в следующей записи:

(2.7)

(2.8)

(2.9)

Чтобы задача (2.7) – (2.8) имела решение, системе её ограничений (2.8) должна быть совместной. Это возможно, если r этой системы не больше числа неизвестных n. Случай r>n вообще невозможен. При r=n система имеет единственное решение, которое будет при оптимальным. В этом случае проблема выбора оптимального решения теряет смысл. План , при котором целевая функция задачи принимает свое максимальное (минимальное) значение, называется оптимальным. Совокупность чисел , удовлетворяющих ограничениям задачи ,называется допустимым решением (или планом).

2. Производственная задача. Ресурсные ограничения. Смысл целевой функции.

6. Теоремы двойственности. Нахождение решения дв. Задачи в симплекс-таблице прямой задачи.

Первая основная теорема двойственности.

1.Если одна из двойственных задач имеет оптимальное решение , то и вторая имеет оптимальное решение этом

2. Если одна из задач неразрешима из-за неограниченности целевой функции

 , то область допустимых решений второй задачи -пустая.

Из доказательства теоремы следует, что - матрица, обратная

к матрице составленной из векторов оптимального базиса, а с_б - вектор-строка коэффициентов в целевой функции при базисных переменных оптимального плана.

Вторая основная теорема двойственности. (теорема о дополняющей нежёсткости). Для того, чтобы 2 допустимых решения и  пары двойственных задач были их оптимальными решениями необходимо и достаточно, чтобы они удовлетворяли системе уравнений:

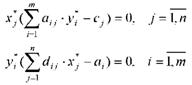
Условия дополняющей нежёсткости важны с точки зрения экономического анализа. Так, если в оптимальном решении двойственной

задачи  . То есть соответствующий г-й ресурс

использован полностью и наоборот, если , то оценка этого ресурса

у_г = 0. Таким образом, оценки  выступают как мера дефицитности

соответствующего ресурса.

Третья основная теорема двойственности (теорема об оценках). Значения у^оптв оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов матрицы основных ограничений исходной задачи на экстремальное значение её целевой функции.

Общая схема симплекс-метода состоит из следующих основных шагов.

 шаг 0. Определение начального базиса  и соответствующей ему начальной угловой точки (базисного плана) .

шаг 1. Проверка текущего базисного плана на оптимальность. Если критерий оптимальности выполнен, то план оптимален и решение закончено. Иначепереход на шаг 2.

шаг 2. Нахождение переменной, вводимой в состав базисных. (Из условия увеличения целевой функции). шаг 3. Нахождение переменной, исключаемой из состава базисных переменных (Из условия сохранения ограничений задачи).

 шаг 4. Нахождение координат нового базисного плана (смежной угловой точки). Переход на шаг 1.

Повторяющиеся шаги 1-4 образуют одну итерацию симплекс-метода.