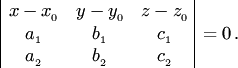19. Вычисление ранга методом Гаусса.

Следующие преобразования матрицы называют элементарными:

перестановка местами строк (или столбцов) матрицы;

умножение всех элементов какой-либо строки (столбца) матрицы на произвольное число k, отличное от нуля;

прибавление к элементам какой-либо строки (столбца) соответствующих элементов другой строки (столбца) матрицы, умноженных на произвольное число k.

Нахождение ранга матрицы с помощью элементарных преобразований матрицы основано на утверждении: если матрица В получена из матрицы А с помощью конечного числа элементарных преобразований, то Rank(A) = Rank(B).

Суть метода элементарных преобразований заключается в приведении матрицы, ранг которой нам требуется найти, к трапециевидной (в частном случае к верхней треугольной) с помощью элементарных преобразований.

Для чего это делается? Ранг матриц такого вида очень легко найти. Он равен количеству строк, содержащих хотя бы один ненулевой элемент. А так как ранг матрицы при проведении элементарных преобразований не изменяется, то полученное значение будет рангом исходной матрицы.

20. Теорема Кронекера-Капелли.

21. Решение системы уравнений методом Гаусса.

См. 7

22. Векторы в трехмерном пространстве. Операции над векторами.

23. Проекция вектора на прямую. Проекция суммы векторов и произведения вектора на число

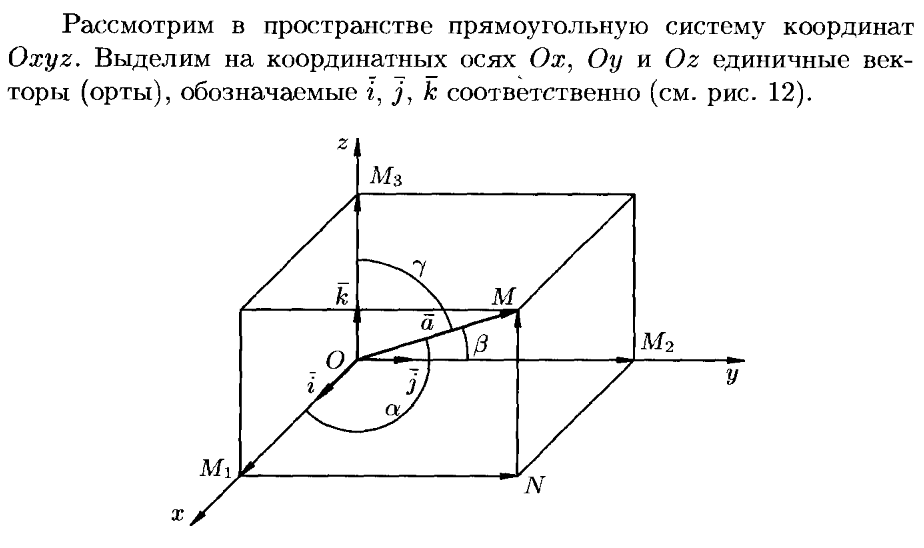
24. Прямоугольная система координат. Орты.

Разложение вектора по ортам, единственность, координаты вектора.

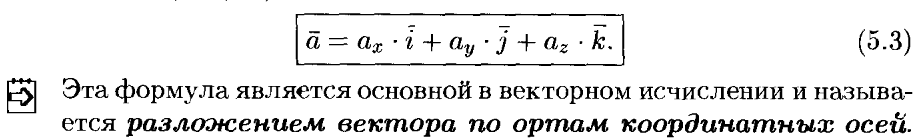
25. Коллинеарные векторы. Условие коллинеарности.

Необходимым и достаточным условием коллинеарности ненулевого вектора   и вектора   является существование такого числа  , которое удовлетворяет равенству 

26. Координаты суммы, разности, произведения на число.

27. Скалярное произведение. Свойства скалярного произведения.

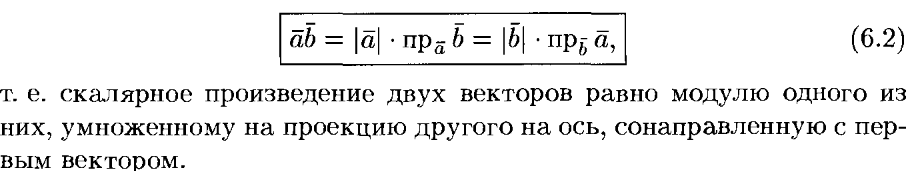
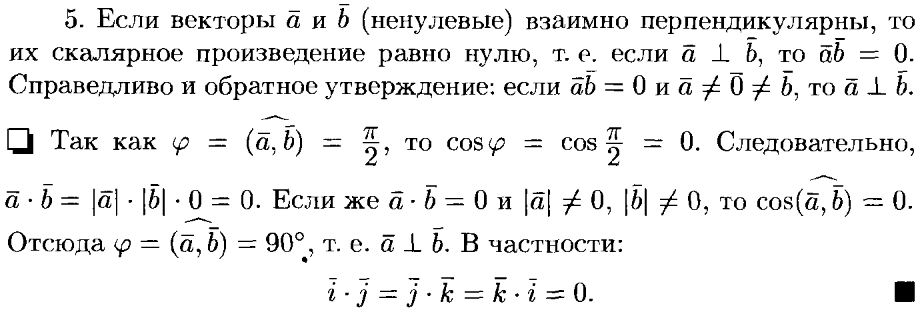
28. Выражение скалярного произведения через координаты векторов.

Угол между векторами. Условие ортогональности векторов

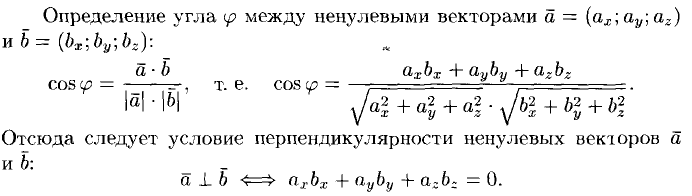
29. Векторное произведение и его свойства.

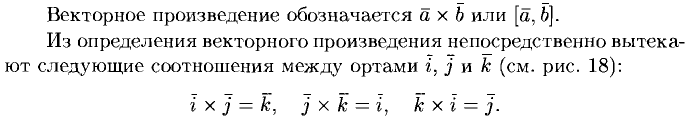
30. Выражение векторного произведения через координаты векторов.

29. Смешанное произведение и его свойства.

30. Геометрический смысл смешанного произведения.

31. Выражение смешанного произведения через координаты векторов.

Условие компланарности трех векторов.

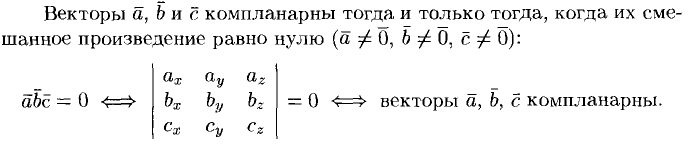
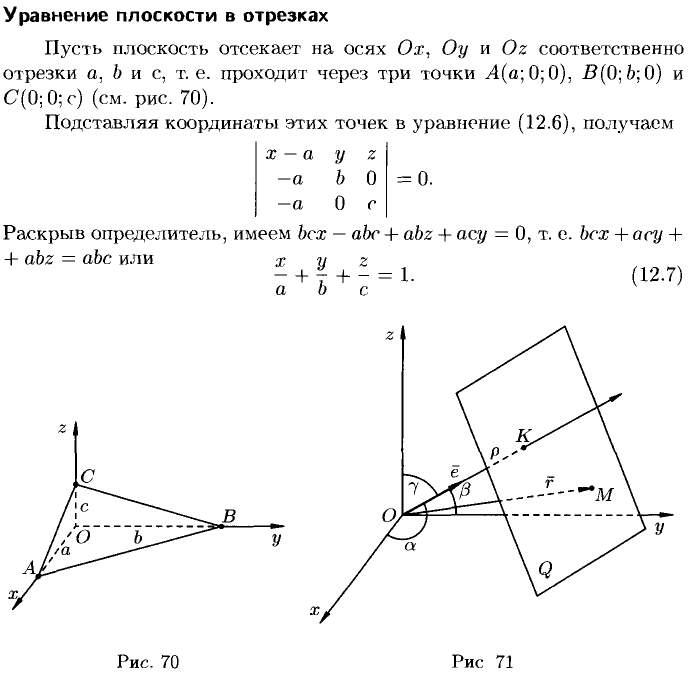
32. Уравнения прямой на плоскости по точке и направляющему вектору, по двум точкам,

в отрезках.

Если известна некоторая точка  , принадлежащая прямой, и направляющий вектор   этой прямой, то уравнение данной прямой можно составить по формуле:

Иногда его называют каноническим уравнением прямой.

33. Уравнение прямой на плоскости по точке и нормальному вектору.

Нормальное уравнения прямой на плоскости. Параметрическое уравнение прямой.

Общее уравнение прямой.

Параметрические уравнения прямой могут быть записаны следующим образом

x = l t + x0

y = m t + y0

где (x0, y0) - координаты точки лежащей на прямой, {l, m} - координаты направляющего вектора прямой.

34. Расстояние от точки до прямой.

35. Уравнение плоскости в пространстве по точке и двум направляющим векторам,

по трем точкам, в отрезках.

Направляющими векторами плоскости называются два неколлинеарных вектора, компланарных этой плоскости, т.е. принадлежащих плоскости или параллельных ей.

Пусть в координатном пространстве   заданы:

а) точка  ;

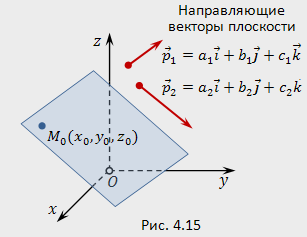
б) два неколлинеарных вектора  (рис.4.15).

Требуется составить уравнение плоскости, компланарной векторам   и проходящей через точку 

Выберем на плоскости произвольную точку  . Обозначим    — радиус-векторы точек   и   (рис.4.16).

Условие компланарности векторов   (рис.4.16) можно записать, используя свойства смешанного произведения   Применяя формулу (1.17), получаем уравнение плоскости, проходящей через заданную точку и компланарной двум неколлинеарным векторам: