1. Матрицы. Сумма, произведение на число, произведение матриц.

2. Свойства произведения матриц.

1. Свойство ассоциативности умножения матриц  .

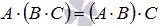2. Два свойства дистрибутивности 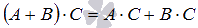  и  .

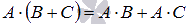3. В общем случае операция умножения матриц некоммутативна  .

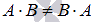4. Единичная матрица Е порядка n на n является нейтральным элементом по умножению, то есть, для произвольной матрицы А порядка p на n справед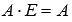ливо  , а для произвольной матрицы А порядка n на p справедливо 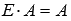 Следует отметить, что при подходящих порядках произведение нулевой матрицы О на матрицу А дает нулевую матрицу. Произведение А на О также дает нулевую матрицу, если порядки позволяют проводить операцию умножения матриц.

4. Транспонированная матрица. Действия над транспонированными матрицами

5. Перестановки, четные и нечетные перестановки. Определение определителя.

Вычисление определителей второго и третьего порядка.

Перестановкой чисел 1, 2,..., n называется любое расположение этих чисел в определенном порядке. Говорят, что в данной перестановке числа i и j составляют инверсию (беспорядок), если i>j, но i стоит в этой перестановке раньше j, то есть если большее число стоит левее меньшего. Перестановка называется четной (или нечетной), если в ней соответственно четно (нечетно) общее число инверсий.

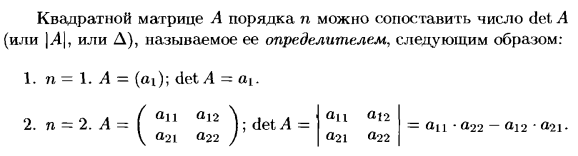
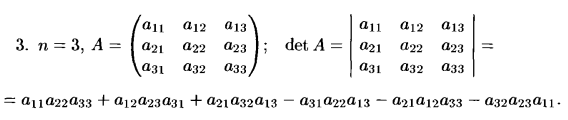
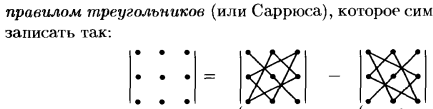
6. Свойства определителей

7. Вычисление определителя методом Гаусса.

8. Алгебраические дополнения элементов определителя.

Разложение определителя по строке или столбцу

9. Обратная матрица. Существование обратной матрицы.

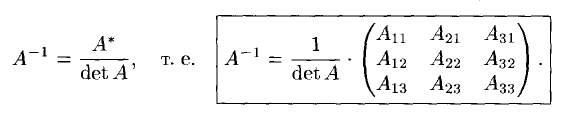
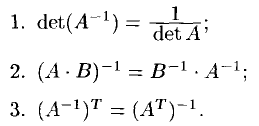
10. Определитель Вандермонда.

Определителем Вандермонда называется определитель

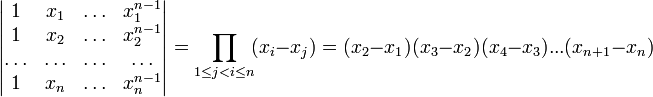
Он равен нулю тогда и только тогда, когда   для некоторых  .

11. Миноры, разложение определителя по группе строк или столбцов.

См. 8

12. Определитель произведения матриц.

Пусть   и   — квадратные матрицы одного и того же порядка. Тогда

т.е. определитель произведения матриц равен произведению их определителей.

Доказательство теоремы проводится в три этапа. Во-первых, теорема справедлива, если один из сомножителей имеет простейший вид (см. рис. 1.6). Пусть, например, матрица   квадратная л-го порядка имеет простейший вид:  . Если  , то в произведении   последние   строк будут нулевыми. Тогда по свойствам 1,2 определителей:   и  , т.е. равенство (2.6) верно. Если же  , то   — единичная матрица. Тогда

т.е. равенство (2.6) справедливо. Аналогично рассматривается случай, когда матрица   имеет простейший вид.

Второй этап — доказательство формулы (2.6) для элементарных матриц. Если матрица   элементарная вида (1.1), (1.3) или (1.5), то ее определитель равен   или 1 соответственно, а произведение   есть элементарное преобразование столбцов матрицы  . По свойствам 1, 3, 6 или 9 определителей убеждаемся в справедливости (2.6). Аналогично рассматривается случай, когда матрица   элементарная вида (1.2), (1.4), (1.6).

Третий этап — доказательство формулы (2.6) для произвольных квадратных матриц n-го порядка. По теореме 1.2 любую квадратную матрицу можно представить в виде произведения простейшей (она является элементарной) и элементарных преобразующих матриц:

 и  . Тогда, используя результат первых двух этапов, можно записать что и требовалось доказать.