Билет 1. Вопрос 1. Световая волна: уравнение, основные параметры и свойства.

ϕ- полная фаза волны

Ψ= ωt-kx+ϕ0; ω-частота, t-время, х- координата, к-квантовое число.

Длина волны- расстояние между двумя последовательными точками волны колебающимися в одной фазе.

.

Фазовая скорость эл.магнитной волны ниже чем в вакууме в n раз, т.е волна тормозит:

; - длина волны в вакууме.

Поток енергии эл.волны зависит от св-в Е и Н.

Плоская волна: - векторное произведение, величина направленная.

Большинство физиологических реакций живых организмов опред. Колебаниями электрического поля.

- уравнение плоской световой волны.

Фронт волны- геометрическое место точек разделяющее на две части пространство до которого возмущение уже дошло и то до которого не дошло.

Волны бывают сферические и плоские. Плоские- все точки фронта волны колеблются в одной фазе и движутся в одном направлении: –цвет ;

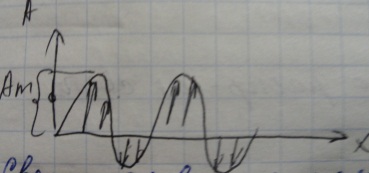
Свет называют поляризованным- если колебания светового вектора в пространстве упорядочены каким либо образом.

1- плоско- поляризованный свет;2- с круговой поляризацией;3- с электрической поляризацией.

Билет 1. Вопрос 2. Осуществление неуправляемой и управляемой ядерных реакций

Ядерная реакция – это процесс взаимодействия атомного ядра с другим ядром или элементарной частицей, сопровождающийся изменением состава и структуры ядра и выделением вторичных частиц или γ-квантов. В результате ядерных реакций могут образовываться новые радиоактивные изотопы, которых нет на Земле в естественных условиях. Первая ядерная реакция была осуществлена Э. Резерфордом в 1919 году в опытах по обнаружению протонов в продуктах распада ядер (см. § 9.5). Резерфорд бомбардировал атомы азота α-частицами. При соударении частиц происходила ядерная реакция, протекавшая по следующей схеме:

  При ядерных реакциях выполняется несколько законов сохранения: импульса, энергии, момента импульса, заряда. В дополнение к этим классическим законам сохранения при ядерных реакциях выполняется закон сохранения так называемого барионного заряда (то есть числа нуклонов – протонов и нейтронов). Выполняется также ряд других законов сохранения, специфических для ядерной физики и физики элементарных частиц. Ядерные реакции могут протекать при бомбардировке атомов быстрыми заряженными частицами (протоны, нейтроны, α-частицы, ионы). Первая реакция такого рода была осуществлена с помощью протонов большой энергии, полученных на ускорителе, в 1932 году:

  Однако наиболее интересными для практического использования являются реакции, протекающие при взаимодействии ядер с нейтронами. Так как нейтроны лишены заряда, они беспрепятственно могут проникать в атомные ядра и вызывать их превращения. Выдающийся итальянский физик Э. Ферми первым начал изучать реакции, вызываемые нейтронами. Он обнаружил, что ядерные превращения вызываются не только быстрыми, но и медленными нейтронами, движущимися с тепловыми скоростями. Ядерные реакции сопровождаются энергетическими превращениями. Энергетическим выходом ядерной реакции называется величина

Q=(MA+MB–MC–MD)c2=ΔMc2.

где MA и MB – массы исходных продуктов, MC и MD – массы конечных продуктов реакции. Величина ΔM называется дефектом масс. Ядерные реакции могут протекать с выделением (Q > 0) или с поглощением энергии (Q < 0). Во втором случае первоначальная кинетическая энергия исходных продуктов должна превышать величину |Q|, которая называется порогом реакции. 

Осуществление управляемых термоядерных реакций даст человечеству новый экологически чистый и практически неисчерпаемый источник энергии. Однако получение сверхвысоких температур и удержание плазмы, нагретой до миллиарда градусов, представляет собой труднейшую научно-техническую задачу на пути осуществления управляемого термоядерного синтеза.

На данном этапе развития науки и техники удалось осуществить только неуправляемую реакцию синтеза в водородной бомбе. Высокая температура, необходимая для ядерного синтеза, достигается здесь с помощью взрыва обычной урановой или плутониевой бомбы.

Термоядерные реакции играют чрезвычайно важную роль в эволюции Вселенной. Энергия излучения Солнца и звезд имеет термоядерное происхождение.

Билет 2.вопрос 1. Основные законы геометрической оптики

1 з-н. закон прямолинейного распространения света.

2 з-н. закон независимости световых лучей-лучи при пересечении не возмущают друг друга и не мешают распространяться друг другу.

3 з-н. закон отражения-падающий луч,отраженный луч,нормаль восстановленная в точке падения луча,лежит в одной плоскости при этом угол падения равен углу отражения.

4 з-н. закон преломления-падающий луч,преломленный луч и нормаль границы раздела лежат в одной плоскости при этом отношение синуса угла падения к синусу угла преломления есть величина постоянная для данной группы веществ.

з-н Снемгуса:

n*sin a=const

n12=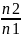 – относительный показатель преломления 2-ой среды по отношению к 1-ой.

Билет 2. Вопрос 2. Радиоактивность.

РАДИОАКТИВНОСТЬ самопроизвольное превращение атомов одного элемента в атомы других элементов, сопровождающееся испусканием частиц и жесткого электромагнитного излучения.

Явление радиоактивности, или спонтанного распада ядер, была открыта французским физиком А. Беккерелем в 1896 г. Он обнаружил, что уран и его соединения испускают лучи или  частицы, проникающие сквозь непрозрачные тела и способные засвечивать фотопластинку, Беккерель установил, что интенсивность излучения пропорциональна только концентрации урана и не зависит от внешних условий (температура, давление) и от того, находится ли уран в каких-либо химических соединениях. Английскими физиками Э. Резерфордом  и Ф. Содди было доказано, что во всех радиоактивных  процессах происходят взаимные превращения атомных ядер химических элементов. Изучение свойств излучения, сопровождающего эти процессы в магнитном и электрическом полях, показало, что оно разделяется на a-частицы (ядра гелия), b- частцы (электроны)  и  g- лучи (электромагнитное излучение с очень малой длиной волны ). Атомное ядро, испускающее g-кванты, a-, b- или другие частицы, называется радиоактивным ядром. В природе существует 272 стабильных атомных ядра. Все остальные ядра радиоактивны и называются радиоизотопами.

Билет 3. Вопрос 1. Интерференция световых волн.

Называется явление наложения световых волн друг на друга, приводящие к образованию устойчивой картины из чередующихся максима и минимума освещенности.

Будем считать, что две световые волны одинаковой частоты приходят в одну и туже точку пространства. Что будет происходить в точке наблюдения?

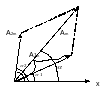
при t=0

При условии, что частоты волн одинаковы, а разность фаз между ними не зависит от времени в точках наблюдения будет устойчивое колебание. Такие волны называются когерентными волнами.

, тогда

Билет 3. Вопрос 2. Деление ядер

Деле́ние ядра́ — процесс расщепления атомного ядра на два (реже три) ядра с близкими массами, называемых осколками деления. В результате деления могут возникать и другие продукты реакции: лёгкие ядра (в основном альфа-частицы), нейтроны и гамма-кванты. Деление бывает спонтанным (самопроизвольным) и вынужденным (в результате взаимодействия с другими частицами, прежде всего, с нейтронами). Деление тяжёлых ядер — экзотермический процесс, в результате которого высвобождается большое количество энергии в виде кинетической энергии продуктов реакции, а также излучения. Деление ядер служит источником энергии в ядерных реакторах и ядерном оружии.

Механизм деления

Процесс деления может протекать только в том случае, когда потенциальная энергия начального состояния делящегося ядра превышает сумму масс осколков деления. Поскольку удельная энергии связи тяжёлых ядер уменьшается с увеличением их массы, это условие выполняется почти для всех ядер с массовым числом .

Билет 4. Вопрос 1. Пространственная и временная когерентность волн

время, за которое случайное изменение фазы достигает значения За время t колебание как бы забывает свою первоначальную фазу и становится некогерентным по отношению к самому себе. Время ~П когерентности световой волны, испу­скаемой таким источником, ~10^-8 сек. Время когерент­ности называют также продолжительностью цуга волн. За время t волна проходит путь сt, кото­рый представляет собой длину цуга (иногда эту вели­чину называют длиной когерентности). На длине цуга случайные изменения фазы достигают величины При т ~ 10^-8 сек длина цуга составляет ~3 м.

Ко­лебания в двух точках «волновой поверхности», отстоя­щих друг от друга на расстояние, меньшее l, будут при­близительно когерентными. Такого рода когерентность называется пространственной. Все пространство, зани­маемое волной, можно разбить на части, в каждой из которых волна сохраняет когерентность. Объем такой части пространства, называемый объемом коге­рентности, по порядку величины равен произведе­нию длины цуга на площадь круга диаметра l.

Пространственная когерентность световой волны вблизи поверхности излучающего ее нагретого тела ограничивается размером l всего в несколько длин волн. Это вызвано тем, что разные участки нагретого тела излучают независимо друга от друга. По мере удаления от источника степень пространственной когерентности возрастает.

Кратко можно сказать, что когерентностью назы­вается согласованное протекание нескольких колеба­тельных или волновых процессов.

∆t=10^-8c-время сброса энергии атома

L=c∆t=3*10 (м/c)* 10^-8 (c)=3м-длина цуга волн

Цуга волн- распределение световой энергии

∆t - продолжительность цуга волн(время когерентности)

Lк –длина когерентности

Vк- объем когерентности

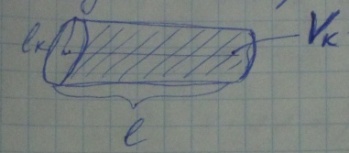
Для получения интер-ой картины необходимо от естественных источников света, необходимо чтоб источник был всего 1 и оптическая разность хода не превысила 3м.

1. Опыт юнга

Билет 4. Вопрос 2. Физика атомов и молекул: атом водорода

Атом водорода — физическая система, состоящая из атомного ядра, несущего элементарный положительный электрический заряд, и электрона, несущего элементарный отрицательный электрический заряд. В состав атомного ядра может входить протон или протон с одним или несколькими нейтронами, образуя изотопы водорода. Электрон преимущественно находится в тонком концентрическом шаровом слое вокруг атомного ядра, образуя электронную оболочку атома. Наиболее вероятный радиус электронной оболочки атома водорода в стабильном состоянии равен боровскому радиусу a₀ = 0,529 Å.

En-? Ѱn-? CИ=1/4*ɛ₀*П cгc=1

ⱷ=^cгc-Ze*e/r ∆Ѱ+2m/ħ²*(E-(-Ze²/r))Ѱ=0

решение:

1. En=(-me⁴/2ħ²)*(z²/n²); n=1,2,3… Ѱ_n,l,m(x,y,z) E&P(энергия и импульс взаимосвязаны )

Энергия-Е; момент импульса - М

-модуль момента импульса

l=0,1,2,….,n-1

-направление момента импульса (проекция на ось z)

Mz=ħ*m , m=-l,….,0,…,+l

Вырожденное энергетическое состояние

Кратность вырождения состояния:

1. При n=1-состояние невырожденное

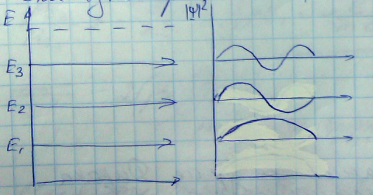
Для однородной ямы (потенциальной)

электрон внутри атома

правило отбора квантовых переходов.

∆l=±1; ∆m=0;±1

Билет 5. Вопрос 1. Принцип Гюйгенса-Фринеля

Принцип устанавливает способ построения фронта волны в момент времени t+Δt если известно положение фронта волны в момент времени t.

Принцип: Каждая точка до которой доходит волновое движение служит центром вторичных волн, огибающая эти вторичные волны и дающая положение фронта волны в следующий момент времени.

Билет 5. Вопрос 2.Модель атома Томпсона.

Модель Томсона представляла собой равномерно заряженную положительным зарядом сферу, в которой вращались или покоились электроны (корпускулы, как их называл Томсон). Поскольку атом в целом нейтрален, то общий заряд электронов равен положительному заряду сферы. Объем сферы гораздо больше объема корпускулы. Электроны вращаются по круговым орбитам, расположенным на различных расстояниях от центра сферы, зависящих от скорости электронов. При некоторой скорости корпускулы достигают поверхности сферы, а дальнейшее увеличение скорости заставляет их покидать сферу. Это означает, что атом распался. Томсон заключает, что атом устойчив тогда, когда кинетическая энергия корпускул не превышает некоторой предельной величины.

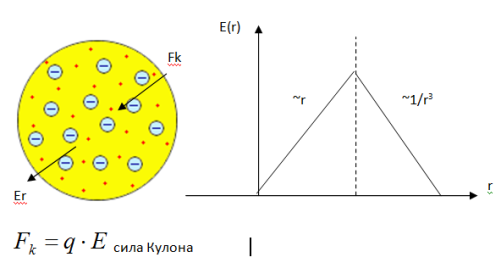
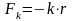
Гармонические колебания

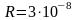
Билет 6. Вопрос 1.Зоны Френеля

Волновой зоной Френеля называются воображаемые части волновой поверхности, колебание которых в точке наблюдения Р отличается по фазе на π радиан при последовательном их переборе.

Площадь m-ной зоны:

Поперечный размер зоны r_m:

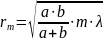
A₁, A₂, A₃…A_m

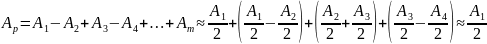
Оказывается воздействие всего волнового фронта S, в точке наблюдения, будет точно такое же, которое оказывает половина первой (центральной) зоны Френеля.

a = 1м; b = 1м; m = 1м; λ = 0,5мкм

- амплитудная пластинка Френеля

– фазовая пластинка Френеля

Амплитудная пластинка Френеля

фазовая пластинка Френеля

Билет 6. Вопрос 2.Ядерная модель атома – модель Резерфорда

Планетарная модель атома, или модель Резерфорда - историческая модель строения атома, которую предложил Эрнест Резерфорд в результате эксперимента с рассеянием альфа-частиц. По этой модели атом состоит из небольшого положительно заряженного ядра, в котором сосредоточена почти вся масса атома, вокруг которого движутся электроны, - подобно тому, как планеты движутся вокруг Солнца. Планетарная модель атома соответствует современным представлениям о строении атома с учётом того, что движение электронов имеет квантовый характер и не описывается законами классической механики. Исторически планетарная модель Резерфорда пришла на смену «модели сливового пудинга» Джозефа Джона Томсона, которая постулирует, что отрицательно заряженные электроны помещены внутрь положительно заряженного атома.

Новую модель строения атома Резерфорд предложил в 1911 году как вывод из эксперимента по рассеянию альфа-частиц на золотой фольге, проведённого под его руководством. При этом рассеянии неожиданно большое количество альфа-частиц рассеивалось на большие углы, что свидетельствовало о том, что центр рассеяния имеет небольшие размеры и в нём сосредоточен значительный электрический заряд. Расчёты Резерфорда показали, что рассеивающий центр, заряженный положительно или отрицательно, должен быть по крайней мере в 3000 раз меньше размера атома, который в то время уже был известен и оценивался как примерно 10^-10 м. Поскольку в то время электроны уже были известны, а их масса и заряд определены, то рассеивающий центр, который позже назвали ядром, должен был иметь противоположный электронам заряд. Резерфорд не связал величину заряда с атомным номером. Этот вывод был сделан позже. А сам Резерфорд предположил, что заряд пропорционален атомной массе.

Недостатком планетарной модели была её несовместимость с законами классической физики. Если электроны движутся вокруг ядра как планеты вокруг Солнца, то их движение ускоренное, и, следовательно, по законам классической электродинамики они должны были бы излучать электромагнитные волны, терять энергию и падать на ядро. Следующим шагом в развитии планетарной модели стала модель Бора, постулирующая другие, отличные от классических, законы движения электронов. Полностью противоречия электродинамики смогла решить квантовая механика.

Высокая монохромотичность пучка α – частиц ; V₀ = const

m, r – любые; Е_к – любая

Спектр излучения сплошной

Модель Томсона представляла собой равномерно заряженную положительным зарядом сферу, в которой вращались или покоились электроны (корпускулы, как их называл Томсон). Поскольку атом в целом нейтрален, то общий заряд электронов равен положительному заряду сферы. Объем сферы гораздо больше объема корпускулы. Электроны вращаются по круговым орбитам, расположенным на различных расстояниях от центра сферы, зависящих от скорости электронов. При некоторой скорости корпускулы достигают поверхности сферы, а дальнейшее увеличение скорости заставляет их покидать сферу. Это означает, что атом распался. Томсон заключает, что атом устойчив тогда, когда кинетическая энергия корпускул не превышает некоторой предельной величины.

Билет 7. Вопрос 1.Дифракция Френеля на круглом отверстии

Сферическая волна в ближней зоне

от источника

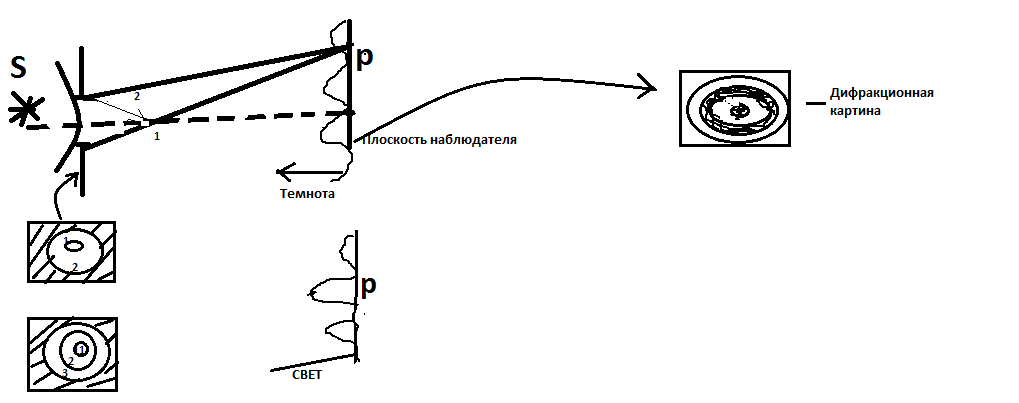
При дифракции Френеля на круглом отверстии дифракционная картина представляет из себя набор чередующихся светлых и тёмных колец, при этом в центре картины наблюдается светлое пятно (если m- нечётное число) или тёмное пятно (если m – чётное).

m – количество зон Френеля уместившихся в пределах отверстия.

Билет 7. Вопрос 2. Волновые свойства вещества. Волны Де-Бройля.

Дуализм свойств электрона : ( материальная точка волновой процесс) => ;

).

1924 г. Луи де Бройль

– длина волны де Бройля.

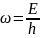
Девисон и Джернер.

Билет 8. Вопрос 1. Дифракция Фраунгофера от щели.

Дифракционная картина при прохождении плоской волны на щели представляет из себя набор чередующихся светлых и темных поло, причём в центре картины находится всегда светлая полоса.

max: ∆ = ±mλ; a*sin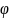 =±mλ где m= 0,1,2… - номер дифракционных зон.

По определению зоны Френеля лучи, идущие от краев каждой зоны, должны иметь разность хода, равную половине длины волны .

Схема хода лучей при дифракции параллельного пучка света (дифракции Фраунгофера) на узкой щели: 1 – непрозрачный экран с щелью; 2 – линза; 3 – экран для наблюдения распределения интенсивности света

График распределения интенсивности света

Дифракционный спектр

Дифракционная решетка

Билет 8. Вопрос 2. Элементарная Боровская теория водородного атома.

1.равномерное вращение

2.стационарная орбита

m*ⱱ*r = , где m*ⱱ*r – уловие стационарности орбиты, 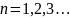-главное квантовое число

2 закон Ньютона m*a=F

СГС => F =

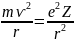
Внутренняя энергия Е_к эектрона + Е_к ядра + Е потенциальная

m_p m_c

Полная энергия атома отрицательная величина

Полная энергия атома:

n=1,2,3…

Главное квантовое число определяет дискритизацию полно энергии атома.

Билет 9. Вопрос 1 Уравнение глограммы и её физ. смысл

Голография (в дословном переводе – полная запись) – способ записи и восстановления волнового поля, основанный на регистрации интерференционной картины, образованной предметной волной (идущей от объекта) и когерентной с ней опорной волной.

Пусть S = s exp(iφs) – комплексная амплитуда световой волны, приходящей в

плоскость голограммы от объекта, и R = r exp(iφr) – комплексная амплитуда опорной волны в плоскости голограммы Н

Тогда для интенсивности интерференционной картины, регистрируемой в плоскости

голограммы, получим:

I = |S+ R| 2 = |S| 2+ |R| 2 + SR* + S*R

Комплексные амплитуды дифрагированных волн в плоскости голограммы пропорциональны произведению комплексной амплитуды освещающей волны

C = с exp(iφC)

на записанные выше интерференционные члены функции пропускания:

Ct ~ C(RS* + R*S) ,

Первый из этих членов, содержащий S*, соответствует действительному

изображению, в то время как второй член, содержащий S, образует мнимое изображение.

Если восстанавливающая волна идентична опорной C = R, то

R I = R (|S|² + |R|²)+ SR*R + S*R R

это и есть основное уравнение голографии.

Из него видно, что SR*R – копия предметной волны (с точностью до множителя);

S*R R – так называемая сопряженная волна (например, если S – расходящаяся сферическая волна, то S* - сходящаяся волна).

Билет 9. Вопрос 2 Постулаты Бора

1913г

1. Из бесконечного множества электронных орбит возможных с точки зрения классической механики в действительности осуществляется только некоторые дискретные орбиты, которые удовлетворяют определённым квантовым уровням ē находящимся на одной из этих орбит не излучает эл. маг. волн несмотря что движутся с ускорением.

2. Излучение испускается или поглощается в виде кванта энергии, при переходе ē из одного станционного состояния в другое, величина кванта = разности энергий тех станционных состояний, между которыми совершился квантовый скачёк ē.

hv = E_m – E_n

Опыт Франка и Герца

 Определялась зависимость тока через гальванометр  от разности потенциалов между катодом и сеткой U. В эксперименте была получена зависимость, изображенная на рис. ЗдесьU = 4,86 В – соответствует первому потенциалу возбуждения. Таким образом, Ф.- Г. о. показал, что спектр поглощаемой атомом энергии не непрерывен, а дискретен, мин. порция энергии (квант энергии), к-рую может поглотить атом Hg, равна 4,9 эВ.

Билет 10. Вопрос 2. Частица в потенциальной яме

Рассмотрим частицу, находящуюся в потенциальной яме с бесконечно высокими стенками. В этом случае потенциальная энергия частицы имеет вид:

Запишем уравнение Шредингера для одномерного движения частицы вдоль оси Х

Поскольку вне ямы потенциальная энергия обращается в бесконечность, то для того, чтобы выполнялось уравнение Шредингера, необходимо, чтобы вне ямы волновая функция ψ_n(x) обращалась в ноль, т.е. ψ_n (x)=0. Это означает, что в случае ямы с бесконечно высокими стенками частица не может выйти за пределы ямы, поскольку такие стенки являются непроницаемыми для частицы. В силу непрерывности волновая функция ψ_n (x)должна обращаться в нуль и на границах ямы: при X=0 и при X=a.

Таким образом, задача о движении частицы в яме сводится к решению уравнения

С граничными условиями

Решение

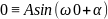ψ(a)=0;

n=1, 2, 3… (целое число)

возведём обе части уравнения в квадрат

n=1, 2, 3…

n-главное квантовое число (показывает дискретизацию полной энергии квантовых частиц )

Отметим, что решение уравнения Шредингера само по себе к квантованию энергии не приводит, квантование возникает из-за граничных условий, накладываемых на волновую функцию, т.е. из-за равенства нулю волновой функции на границе потенциальной ямы.

Уравнение нормировки

n=1, 2, 3…

Графики волновых функций ψ_n (x) для первых четырех значений квантового числа n приведены на рисунке

Волновые функции, отвечающие разным значениям n, существенно отличаются друг от друга. Если поместить начало координат в середину ямы, то волновые функции частицы внутри ямы для нечетных значений n будут четными функциями координаты x, и наоборот, волновые функции для четных n- нечетными функциями координаты. При увеличении квантового числа n на единицу число точек пересечения волновой функции с осью x также увеличивается на единицу.

На рисунке представлены графики квадрата модуля волновой функции, определяющего плотность вероятности нахождения частицы в яме:

Плотность вероятности оказывается существенно различной для разных состояний частицы, т.е. для разных значений квантового числа n. Так, например, в основном состоянии, т.е. при n=1, частица с наибольшей вероятностью находится в центре ямы. А в первом возбужденном состоянии, т.е. при n=2, вероятность обнаружить частицу в центре ямы равна нулю, хотя пребывание частицы в левой и правой половинах ямы равновероятно.

Билет 11. Вопрос 1. Естественный и поляризованный свет

Условия формирования света с круговой поляризацией:

И поляризованный и естественный свет можно представить моделью, состоящей из двух плоских поляризованных волн, идущих в одном направлении с фиксированным смещением по фазе. Если разность фаз во времени меняется случайно, то такая модель описывает естественный или не поляризованный свет.

Билет 11. Вопрос 2. Масса и энергия связи ядра.

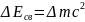
Удельная энергия связи:

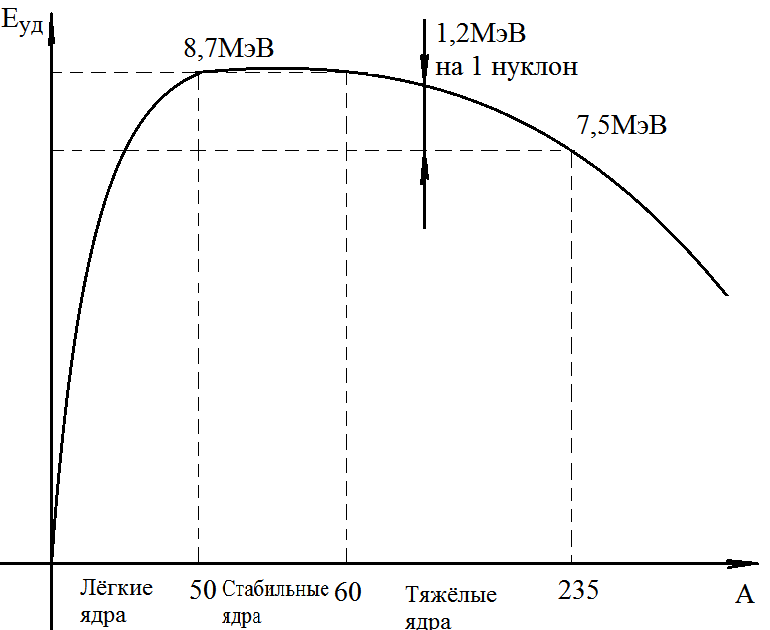
На 1 кулон может быть затрачено max 8,7 МэВ энергии

Деление ядер:

Синтез ядер:

1)Разогнать, что бы “слиплись» частицы

2)Нареть объём с ядрами элементов (термоядерный синтез) t=5000/6000 K

Билет 13. Вопрос 1.Способы получения поляризованных лучей

- использование анизотропных кристаллов

Структура и св-ва кристалла в разных направлениях отличаются друг от друга

n_x≠n_y; V=c/n; V_x≠V_y

- Эффект двойного лучепреломления

- Явление поляризации при отражении и преломлении света

tg_ib=n₁₂>n₂/n₁ - закон полной поляризации

- Поляризация при рассеянии света

Рассеяние света на частицах, размеры которых значительно меньше длинны волны

- В анизотропных жидкостях

t=10^-8c - оптический затвор

Билет 13. Вопрос 2. Атомное ядро. Состав и хар-ки нуклонов

Ядро: протоны, нейтроны (нуклоны)

Протон (р) ядро атома водорода

Заряд е₊ Масса m_p=18368* m_e

E = mc² = > m_p = 938.2 МэВ 1эВ = 1.6*10^-19Дж m_e = 0.511 МэВ S = ½ μ_р=+2.79*μ_о

μ_о – ядерный магниток

Нейтрон (n)

Заряд о

Масса m_n =939.5 МэВ; m_n – m_p = 2.5 * m_e S = ½

Собственный магнитный момент μ_n=-1.91*μ_о

Билет №14.Вопрос .1 Тепловое излучение: общая хар-ка и отличие от люминисценции.

Теплово́е излуче́ние или лучеиспускание — передача энергии от одних тел к другим в виде электромагнитных волн за счёт их тепловой энергии. Тепловое излучение в основном приходится на инфракрасный участок спектра, т.е на длины волн от 0,74 мкм до 1000 мкм. Отличительной особенностью лучистого теплообмена является то, что он может осуществляться между телами, находящимися не только в какой-либо среде, но и вакууме.

Примером теплового излучения является свет от лампы накаливания.

- тепловое равновесие с окр. Средой

1) Равновесное излучение (сколько тело отдает, столько и получает из окр. Среды)

2) Электролюминисценция (свечение под действие эл.света)

3)Химолюминисценция (свечение в результате протекания хим.реакции)

4)Фотолюминисценция (свечение, или на него светит другой свет с большей длиной волны)

Отношение излучательной и поглощательной способностей тел описывается законом излучения Кирхгофа

Закон Кирхгофа для теплового излучения: отношение лучеиспускательной(излучательной) и поглощательной способности тела не зависит от природы тела, оно является для всех тел одной и той же универсальной функцией частоты и температуры.

r_wt/a_wt=f(w,t)

r_wt – лучеиспускательная способность тела(спектральная хар-ка теплового излучения)

r_{wt =} dR_w/dw – спектральная излучательная способность тела

R_w - энергетическая способность тела(поток световой энергии испускаемый с единицы поверхности светящегося объекта)

R_w = w/st

a_wt – спектральная поглощательная способность

a_wt = dФ^lw/dФw

dФ^lw – поглощенная энергия данным телом

dФw – полная падающая энергия на тело

Абсолютно черное тело, a_wt=1

- физическая модель абсолютно черного тела

a_wt < 1 – серое тело

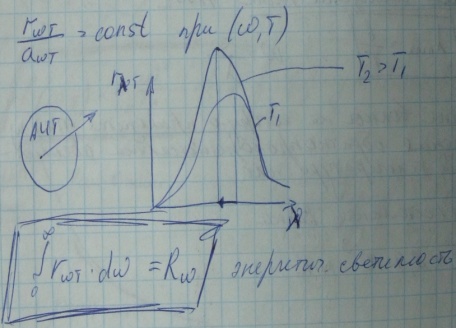
Закон Стефана Больцмана(1884г).

R_э = σ T⁴

σ – постоянная Стефана Больцмана (5,7 * 10^-8 Вт/м²*К⁴)

Закон смещения Вина 1893г

γ _max = b/T w = c/γ

Длина волны на которую приходится max излучения обратно пропорциональна обсалютной температуре тела

b- постоянная Вина ( 2,9 * 10^-3 м*К)

Билет 15. Вопрос 1. Закон Кирхгофа для теплового излучения.

Отношение лучеиспускательной (излучательной) и поглощательной способности тела не зависит от природы тела, оно является для всех тел одной и той же универсальной функцией частоты и температуры

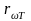- лучеиспускательная способность тела( спектральная хар-ка теплового излучения)

- спектральная излучательная способность тела

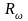- энергетическая светимость тела( поток световой энергии испускаемый с единицы поверхности светящегося объекта)

-спектральная поглощательная способность тела.

-поглощенная энергия данным телом - полная падающая энергия на тело.

при =1

АЧТ-абсолютное черное тело.

-физическая модель АЧТ.

- серое тело

энергетич. светимость

Билет 15. Вопрос 2.Распределение Ферми-Дирака.

ФЕРМИ-ДИРАКА РАСПРЕДЕЛЕНИЕ - функция распределения по уровням энергии тождественных частиц с полу-целым спином при условии, что взаимодействием частиц между собой можно пренебречь.

где W - энергия уровня,  вероятность заполнения которого оп­ре­де­ляется при температуре T; k - постоянная Больцмана.

Си­стемы ми­кро­ча­с­тиц, свойства которых опи­сы­ва­ют­ся рас­пре­­де­ле­нием Ферми-Ди­ра­ка называются вырож­де­н­­ными.

При Т=0 график функции Ферми имеет вид, изображен­ный на рис. а.

Из рис. а и формулы при Т=0 вытекают сле­ду­ю­щие соотношения:

При нагревании металла электронам сообщается тепловая эне­­­р­гия, величина которой определяется произведением kT. Зна­че­­ние этой энергии невелико. Например, при комнатной тем­пе­ра­ту­ре (око­ло 300 К) значение тепловой энергии электронов оп­ре­де­­ля­ет­ся величиной W_т=0,026 эВ. Однако за счет теплового воз­бу­­ж­дения существует вероятность того,  что некоторые эле­к­тро­ны с энер­гией, близкой к энергии уровня Ферми, начинают за­по­л­­­нять со­стояния с более высокой энергией. В результате график фун­­к­ции Ферми при Т=0 теряет ступенчатую форму и становится бо­­лее пологим, как это показано на рис. б. Из формулы (наверху)  для  Т>0 вытекают следующие соотношения:

Из соотношения "в" следует, что вероятность "нахождения" электрона на уровне Ферми составляет 0,5.

При выполнении условия W-W_F >>kT выражение (вверхуформула) для функции распределения Ферми-Дирака переходит в закон распределения Больцмана, т.е:

Билет 16 Вопрос 1. Закон Стефана-Больцмана и закон Вина.

Закон Стефана-Больцмана: 1884г.

Энергия, поступившая к поверхности Солнца (или к поверхности любого горячего объекта), покидает его в виде излучения. Закон Стефана-Больцмана показывает нам, какова излученная энергия. Энергетическая светимость АЧТ (абс-го чёрного тела) пропорциональна 4 степени. АЧТ- тела, которые полностью поглощают упавшее на него излучение всех длин волн.α(λ/T)=1

Rэ= σ*T⁴, где σ-Постоянная Стефана-Больцмана; Т - температура (в кельвинах).

σ=5,7*10^-8 Вт/(м²*К⁴). Из формулы видно, что при повышении температуры светимость тела возрастает в значительно большей степени.

Закон Стефана-Больцмана распространяется только на абсолютно черное тело, поглощающее всё попадающее на его поверхность излучение. Реальные физические тела поглощают лишь часть лучевой энергии, а оставшаяся часть ими отражается.

Закон смещения Вина : 1893г.

Длина волны, на которую приходится max излучение, обратно пропорциональна абсолютной температуре тела.

λ= в/T, где в -постоянная Вина, в=2,9*10^-3 м*к. T-температура.

Температура T₂ больше T₁, с ростом температуры увеличивается интенсивность теплового движения атомов и молекул тела и возрастает энергия, излучаемая телом в виде электромагнитных волн с любыми λ. Поэтому при повышении температуры вся спектральная характеристика поднимается, как это показано на рисунке ниже.w=c/λ.

Билет 16. Вопрос 2.Квантовая теория свободных электроном в металле.

Cогласно квантовым представлениям, энергия электронов в атоме может изменяться дискретным образом. Согласно принципу Паули, в одном квантовом состоянии может находиться не более одного электрона. В результате электроны последовательно заполняют разрешенные энергетические уровни в атоме, формируя его электронные оболочки. При сближении большого числа атомов и образовании кристаллической структуры химические связи между атомами образуются за счет электронов, находящихся во внешних, валентных, электронных оболочках. Согласно принципу Паули, атомы не могут сбиться в плотную массу, поскольку в этом случае в одном квантовом состоянии оказалось бы много частиц с полуцелым спином - собственным моментом количества движения. В результате образуется зона разрешенных энергетических уровней для электронов в твердом теле.  Расстояние между соседними разрешенными уровнями электронов в металлах много меньше энергии  теплового движения электронов даже при самых низких температурах.

Потенциальная энергия электрона в пределах образца металла приблизительно постоянна, но для выхода электрона из металла надо совершить работу против сил электростатического притяжения отрицательного электрона к ионному остатку.

Распределение электронов по энергиям в металле можно представить параболической зависимостью, изображенной на рисунке. Электроны, расположенные в глубине от уровня Ферми, не могут обмениваться энергией с кристаллической решеткой, для них все ближайшие энергетические состояния заняты.

17 билет. Вопрос 1.Формула Релея-Джинса

Теорема о равнораспределении энергии по степеням свободы ТДС.

_{-на одну степень.}

-стоячая волна (возникает за счет набега волн с одной и другой стороны)

-бегущая волна

_{-формула Релея-Джинса.}

”УФ-катастроф” (в реальной жизни не может быть).

Билет 17. Вопрос 2.Формула планка

В 1900г.; квант энергии

Электро-магнитные излучения выполняют в виде кванта энергии.

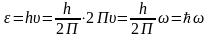_{, где h-постоянная Планка, h=6,626*10-34Дж*с.}

_{-формула Планка}

Билет 18. Вопрос 1. Опыт Боте

Опыт Боте

Опыт Боте (1924 г.). В этом опыте тонкая металлическая фольга Ф освещалась рентгеновскими лучами малой интенсивности, вызывающими в фольге слабую рентгеновскую флюоресценцию (послесвечение). Рентгеновское излучение от фольги попадало на два счетчика ионизирующего излучения Сч1 и Сч2 (счетчики Гейгера). Чувствительность таких счетчиков настолько велика, что они могут регистрировать отдельные рентгеновские кванты. Срабатывая, счетчики приводили в действие механизмы самописцев М1 и М2, делающие отметки на движущейся ленте Л. В результате получено, что отметки на ленте от двух самописцев, связанные с моментами попадания в счетчики рентгеновских квантов, абсолютно случайны. Этот факт можно было объяснить лишь беспорядочным попаданием рентгеновских квантов, рассеиваемых фольгой то в одном, то в другом направлении, тогда как согласно волновым представлениям излучение от источника должно распространяться равномерно во все стороны.

Фотон – носитель порции световой энергии.

Энергия фотона. с

[ ] 10^-10м

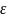[ ] Электрон-Вольт

=

Масса фотона. =

= - Специальная теория относительности (СТО)

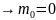– масса покоя.

Фотон существует только в движении.

Импульс фотона. Согласно СТО: E=

Для фотона: c*p

Импульс: p= = = * =

– постоянная планка.

модуль волнового числа.

P= h*k

= F

Давление света количественно рассчитывается

P= (1+p)*n*

p- коэф-т отражения

n –плотность потока фотонов

Билет 18. Вопрос 2. Колебания кристаллической решетки. Фононы

ФОНОН - квант колебаний атомов кристаллической решётки. Рассмотрение колебаний кристаллической решётки основано на адиабатическом приближении, в рамках к-рого совокупности её структурных элементов (атомов, молекул, ионов) можно приписать потенциальную энергию, зависящую от координат ядер. Эта энергия разлагается в ряд по степеням малых смещений ядер из их положения равновесия. Обычно в кристаллах смещения атомов малы вплоть до температуры плавления. Поэтому можно ограничиться гармоническим приближением, т. е. в разложении энергии оставить только квадратичные по смещениям слагаемые.

В гармоническом приближении динамического состояние кристалла описывается совокупностью нормальных колебаний (волн). Каждое нормальное колебание определяется значением волнового вектора k, частота волны w является ф-цией k. В кристалле, элементарная ячейка которого содержит r атомов, существует 3r типов различных нормальных колебаний, отличающихся друг от друга не только зависимостью w(k), но и поляризацией колебаний. В гармоническом приближении колебательная энергия кристалла - сумма энергий нормальных колебаний.

Билет 19. Вопрос 1. Эффект Комптона

Особенно отчетливо проявляются корпускулярные свойства света в явлении, которое получило название э ф ф е к т а К о м п т о н а .

В 1923 г. А. Комптон, исследуя рассеяние рентгеновских лучей различными веществами, обнаружил ,что в рассеянных лучах ,наряду с излучением первоначальной

длины волны К, содержатся также лучи большей длины волны . Разность

оказалась независящей от и от природы рассеивающего вещества. Экспериментально была установлена следующая закономерность :

где — угол, образуемый направлением рассеянного излучения с направлением первичного пучка, — постоянная ,равная .

Схема опыта Комптона показана на рис. 175. Выделяемый диафрагмами Д узкий пучок монохроматического (характеристического) рентгеновского излучения направлялся

на рассеивающее вещество РВ. Спектральный состав рассеянного излучения исследовался с помощью рентгеновского спектрографа, состоящего из кристалла Кр и ионизационной камеры И К.

На рис. 176 приведены результаты исследования рассеяния

монохроматических рентгеновских лучей [линия молибдена] на графите. Кривая а характеризует первичное-излучение. Остальные кривые относятся к разным углам рассеяния значения которых указаны на рисунке. По оси ординат отложена интенсивность излучения, по оси абсцисс — величина, пропорциональная длине волны.

Рис. 177 характеризует зависимость соотношения интенсивностей

смещенной М и несмещенной Р компонент

от атомного номера рассеивающего вещества. Верхняя кривая в левом столбце характеризует первичное излучение (линия Ка серебра). При рассеянии веществами

с малым атомным номером (Li, Be, В) практически все рассеянное излучение имеет смещенную длину волны.По мере увеличения атомного номера все большая часть излучения рассеивается без изменения длины волны.

Все особенности эффекта Комптона можно объяснить , рассматривая рассеяние как процесс упругого столкновения рентгеновских фотонов с практически свободными электронами. Свободными можно считать наиболее слабо связанные с атомами электроны, энергия

связи которых значительно меньше той энергии, которую фотон может передать электрону при соударении1).

Пусть на первоначально покоящийся свободный электрон падает фотон с энергией и импульсом . Энергия

электрона до столкновения равна ( — масса

покоя электрона), импульс равен нулю. После столкновения электрон будет обладать энергией и импульсом связаны соотношением (42.6)]. Энергия и импульс фотона также изменятся и станут равными . Из законов сохранения энергии и импульса вытекают два соотношения:

направлением распространения рассеянного света и направлением первичного пучка.

Вычтя уравнение (58.3) из (58.2), получим:

Приняв во внимание соотношение (42.6), легко убедиться в том, что Таким образом, мы приходим к равенству:

совпадающую с эмпирической формулой (58.1), если положить

Величина

называется ко м и то н о в с ко и д л и н о й в о л н ы той частицы, масса которой имеется в виду. Подстановка численных значений и с дает для комптоновской длины волны электрона значение

Умножив электрона на , получим для значение0,0242 А, совпадающее с эмпирическим значением коэффициента в формуле (58.1).

коэффициента в формуле (58.1).

При рассеянии фотонов на электронах, связь которых с атомом велика, обмен энергией и импульсом происходит с атомом как целым. Так как масса атома намного превосходит массу электрона, комптоновское смещение в этом случае ничтожно и практически совпадает с . По мере роста атомного номера увеличивается относительное число электронов с сильной связью, чем и обусловливается ослабление смещенной линии (см рис.177).

Билет 20. Вопрос 2. Вынужденное излучение

Кроме самопроизвольных (спонтанных) переходов с одного энергетического уровня на другой, наблюдаются также вынужденные (или индуцированные ) переходы, обусловленные действием на атом падающего на него излучения. Самопроизвольные переходы могут осуществляться только в одном направлении — с более высоких уровней на более низкие. Вынужденные переходы могут с равной вероятностью происходить как в одном, так и в другом направлении. В случае перехода на более высокий уровень атом поглощает падающее на него излучение. При вынужденном переходе с одного из возбужденных уровней на более низкий энергетический уровень происходит излучение атомом фотона, дополнительного к тому фотону, под действием которого произошел переход. Это дополнительное излучение называется вынужденным (или индуцированным).

Вынужденное излучение обладает весьма важными свойствами. Направление его распространения в точности совпадает с направлением распространения внешнего излучения, вызвавшего переход. То же самое относится к частоте, фазе и поляризации вынужденного и внешнего излучений. Таким образом, вынужденное и внешнее излучения оказываются когерентными. Эта особенность вынужденного излучения лежит в основе действия усилителей и генераторов света, называемых лазерами (см. § 86).

Вынужденное излучение является обращением процесса поглощения света.

Высокая когерентность излучения открывает широкие перспективы использования лазеров для целей радиосвязи, в частности для направленной радиосвязи в космосе.

-спонтанное самопроизвольное излучение.

Время жизни в возбужденном состоянии – это время за которое число атомов находящиеся в данном возбужденном состоянии уменьшается в е раз( е=2, 71.)

=10^-8-10^-9 с; =0,1 с – мегастабильное.

∆λ-собственная (естественная) ширина спектральной линии.

Г=ħ/ -ширина энергетического уровня

Ширина спектральной линии измеряемая в частотах определяется точно временем жизни δω=1/ =Г/ħ. δ-собственная или естественная. При λ= 5000А̊ = δω=10⁸Гц= δλ=10^-4 А̊.

Эффект Доплера (ω_Д)

Ширина спектральных линий (СЛ)

δω_∑=δω+δ ω_Д

В оптическом диапазоне: ω_Д«δω

Вынужденные (индивидуальные) переходы (W)

Вынужденное излучение состоит из фотонов, которые являются точной копией I фотона, вызвавшего само излучение, т.е. у этих фотонов одинаковая частота, фаза, поляризация и направление.

Билет 21. Вопрос 1. Контактная разность потенциалов

Контактная разность потенциалов, разность электрических потенциалов, возникающая между контактирующими телами в условиях термодинамического равновесия. Наиболее важно понятие. Если два твёрдых проводника привести в соприкосновение, то между ними происходит обмен электронами, причём вначале преимущественно электроны переходят из проводника с меньшей работой выхода в проводник с большей работой выхода. В результате этого процесса проводники приобретают электрические заряды противоположных знаков, что приводит к появлению электрического поля, препятствующего дальнейшему перетеканию электронов. В конечном счёте достигается равновесие, при котором потоки электронов в обоих направлениях становятся одинаковыми.

Билет 21. Вопрос 2. Рентгеновские и молекулярные спектры

МОЛЕКУЛЯРНЫЕ СПЕКТРЫ, спектры испускания и поглощения электромагн. излучения и комбинац. рассеяния света, принадлежащие свободным или слабо связанным молекулам. Имеют вид совокупности полос (линий) в рентгеновской, УФ, видимой и радиоволновой областях спектра. Положение полос (линий) в спектрах испускания и поглощения) характеризуется частотами v длинами волн l = c/v, где с-скорость света и волновыми числами = 1/l; оно определяется разностью энергий Е' и Е: тех состояний молекулы, между которыми происходит квантовый переход:

Вероятность переходов с испусканием или поглощением излучения определяется прежде всего квадратом матричного элемента электрич. дипольного момента перехода, а при более точном рассмотрении - и квадратами матричных элементов магн. и электрич. квадрупольного моментов молекулы. При комбинац. рассеянии света вероятность перехода связана с матричным элементом наведенного дипольного момента перехода молекулы, т.е. с матричным элементом поляризуемости молекулы.

Рентгеновские спектры, спектры испускания и поглощения рентгеновских лучей, т. е. электромагнитного излучения в области длин волн от 10^-4до 10³ Спектр излучения рентгеновской трубки представляет собой наложение тормозного и характеристического Р. с. Тормозной Р. с. возникает при торможении заряженных частиц, бомбардирующих мишень (см. Тормозное излучение). Интенсивность тормозного спектра быстро растет с уменьшением массы бомбардирующих частиц и достигает значительной величины при возбуждении электронами. Тормозной Р. с. — сплошной, так как частица может потерять при тормозном излучении любую часть своей энергии. Он непрерывно распределён по всем длинам волн l, вплоть до коротковолновой границы l₀ = hc/eV .С увеличением порядкового номера Z атомов мишени I также растет.Характеристические Р. с. испускают атомы мишени, у которых при столкновении с заряженной частицей высокой энергии или фотоном первичного рентгеновского излучения с одной из внутренних оболочек (К-, L-, М-... оболочек) вылетает электрон. Состояние атома с вакансией во внутренней оболочке (его начальное состояние) неустойчиво. Электрон одной из внешних оболочек может заполнить эту вакансию, и атом при этом переходит в конечное состояние с меньшей энергией (состояние с вакансией во внешней оболочке). Избыток энергии атом может испустить в виде фотона характеристического излучения. Поскольку энергии E₁начального и E₂ конечного состояний атома квантованы, возникает линия Р. с. с частотой n = (E₁ — E₂)/h.

Билет 22. Вопрос 2. Спин электрона

Для объяснения мультиплетной структуры спектрови аномального эффекта Зеемана (см. § 75) Гаудсмит и Юленбек выдвинули в 1925 г. гипотезу о том, что электрон обладает собственным моментом импульса не связанным с движением электрона в пространстве. Этот собственный момент был назван спином.

Первоначально предполагалось, что спин обусловлен вращением электрона вокруг своей оси. Согласно этим представлениям электрон уподоблялся волчку или веретену. Однако очень скоро пришлось отказаться от подобных модельных представлений, в частности по следующей причине. Вращающийся заряженный шарик должен обладать магнитным моментом, причем отношение магнитного момента к механическому должно иметь значение [см. (71.1)]:

Действительно, было установлено, что электрон, наряду с собственным механическим моментом, обладает также и собственным магнитным моментом . Однако

ряд опытных фактов, в частности аномальный эффект Зеемана, «свидетельствует о том, что отношение собственных магнитного и механического моментов в два раза больше, чем для орбитальных моментов:

. Спин следует считать внутренним свойством, присущим электрону подобно тому, как ему

Величина собственного момента импульса электрона определяется по общим законам квантовой механики так называемым спиновым

квантовым числом s , равным 0,5):

Составляющая механического момента по заданному направлению может принимать квантованные значения, отличающиеся друг от друга на

Чтобы найти величину собственного магнитного момента электрона, умножим Ms на отношение (72.2)

Знак минус указывает на то, что механический и магнитный моменты электрона направлены в противоположные стороны.

Проекция собственного магнитного момента электрона на заданное направление может иметь следующие значения:

Таким образом, проекция собственного момента импульса электрона может принимать значения и , а собственного магнитного момента — значения

.В ряд формул, в частности в выражение для энергии, входят не сами моменты, а их проекции. Поэтому принято говорить, что собственный механический момент (спин) электрона равен половине (подразумевается в единицах ), а собственный магнитный момент равен одному магнетону Бора.

причем j может иметь значения:

где l и s соответственно азимутальное и спиновое квантовые числа. При l = 0 квантовое число j имеет только одно значение: При l, отличном от нуля, возможны

два значения: , которые соответствуют двум возможным взаимным ориентациям моментов — «параллельной» и «антипараллельной»

Билет 23. Вопрос 1 Работа выхода

1)Работа выхода – разница между минимальной энергией, которую необходимо сообщить электрону для его «непосредственного» удаления из объёма твёрдого тела, и энергией Ферми. Здесь «непосредственность» означает то, что электрон удаляется из твёрдого тела через данную поверхность и перемещается в точку, которая расположена достаточно далеко от поверхности по атомным масштабам (чтобы электрон прошёл весь двойной слой), но достаточно близко по сравнению с размерами макроскопических граней кристалла. При этом пренебрегают дополнительной работой, которую необходимо затратить на преодоление внешних полей, возникающих из-за перераспределения поверхностных зарядов. Таким образом, работа выхода для одного и того же вещества для различных кристаллографических ориентаций поверхности оказывается различной.

Работа выхода в внешнем фотоэффекте - минимальная энергия, необходимая для удаления электрона из вещества под действием света

Единицами измерения работы выхода являются Джоуль (Дж) или электронвольт (эВ).

2)Каждый электрон в атоме движется в первом приближении в центрально-симметричном некулоновском поле. Состояние электрона в этом случае определяется тремя квантовыми числами: n и m. Таким образом, состояние каждого электрона в атоме характеризуется четырьмя квантовыми числами:

Энергия состояния зависит в основном от чисел п и д. Кроме того, имеется слабая зависимость энергии от чисел ml и тs поскольку их значения связаны с взаимной ориентацией моментов, от которой зависит величина взаимодействия между орбитальным и собственным магнитными моментами электрона.

В нормальном (невозбужденном) состоянии атома электроны должны располагаться на самых низких доступных для них энергетических уровнях

Совокупность электронов, имеющих одинаковые п и /, образует оболс-чку. Совокупность оболочек с одинаковым п образует группу или слой. В соответствии с значением п слоям дают обозначения, заимствованные из спектроскопии рентгеновских лучей.

Квантовое число проекции результирующего орбитального момента Ml этой оболочки на ось z имеет единственное значение . Следовательно, L также равно нулю.

Билет 23. Вопрос 2. Распределение электронов в атоме по энергетическим уровням. Принцип Паули

Принцип Паули дает объяснение периодической повторяемости свойств атомов. Каждый последующий атом будем получать, увеличивая заряд ядра предыдущего атома на единицу и добавляя к нему один электрон, который мы будем

помещать в доступное ему согласно принципу Паули состояние с наименьшей энергией,

В атоме водорода имеется в основном состоянии один Is электрон с произвольной ориентацией спина. Его квантовые числа: .

Процесс застройки электронных оболочек у элементов периодической системы. Одиннадцатый элемент, натрий, имеет, кроме заполненных слоев К и L, один электрон в оболочке 3s. Электронная конфигурация имеет вид: .

Билет 24. Вопрос 1. Полупроводниковые приборы: диод, транзистор

1)Устройство, которое не пропускает ток в одном направлении и пропускает в противоположном, называется диодом. Существуют различные варианты использования диодов. Например, в устройствах с питанием от батареи часто используется диод для защиты от выхода из строя при несоблюдении полярности подключения этой батареи. При неправильном подключении диод просто не пропускает ток – это защищает чувствительную электронную начинку устройства. При обратном включении напряжения ток идеального диода полностью блокируется. На практике через диод протекает некоторый обратный ток, равный приблизительно 10 микроампер – это немного, но в то же время свидетельствует, что такое устройство не идеально. Если приложить к диоду достаточно высокое обратное напряжение, произойдет пробой перехода и потечет ток. Как правило, напряжение пробоя диода намного превышает напряжения, которые могут возникать во время функционирования схемы, поэтому его воздействие мы подробно рассматривать не будем. При прямом включении требуется совсем маленькое напряжение, чтобы через диод пошел ток. Для кремния такое напряжение приблизительно равно 0,7 Вольта. Это напряжение требуется для того, чтобы на переходе начался процесс комбинации (объединения) электронов и дырок. Транзисторы составляют из трех слоев. Можно создать такой бутерброд вида NPN или PNP. Транзистор может выполнять функции ключа или усилителя. Внешне транзистор похож на два диода, имеющих одну общую точку, в которой они соединены одноименными выводами. Можно ожидать, что ток через транзистор течь не будет, поскольку включенные навстречу друг другу диоды не пропустят ток ни в одном, ни в другом направлении. И это действительно так. Однако если через центральный слой этого бутерброда пропустить маленький ток, сквозь весь бутерброд сможет пройти гораздо больший ток. Благодаря таким свойствам транзистор может использоваться как переключатель. В таком устройстве с помощью небольшого тока можно включать и выключать большой ток. Кремниевый чип представляет собой кусочек кремния, на котором могут разместиться тысячи транзисторов. Используя транзисторы в качестве ключей, можно создать булевы вентили, а из этих вентилей сконструировать микропроцессорные чипы. Естественный переход от кремния к легированному кремнию, а затем к транзисторам и чипам привел к тому, что микропроцессоры и другие электронные устройства в условиях современного общества получили такое широкое распространение и стали такими дешевыми. Фундаментальные принципы построения таких устройств на удивление просты. Удивительно лишь то, что эти принципы постоянно совершенствуются до такой степени, что на сегодняшний день уже удается без больших затрат формировать десятки миллионов транзисторов на одном чипе. В настоящее время в большинстве цифровых устройств, начиная от простых цифровых микросхем и микросхем электронных часов и заканчивая большими интегральными микросхемами компьютерных процессоров, используются полевые транзисторы.

Вопрос 24. Вопрос 2. Волновая функция. Соотношение неопределенности

Волнова́я фу́нкция, или пси-функция  — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису:

где  — координатный базисный вектор, а  — волновая функция в координатном представлении.

Физический смысл волновой функции заключается в том, что согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке конфигурационного пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния в координатном представлении.

Соотношение неопределенностей

Неопределенности координаты и импульса связаны между собой соотношением: , где , h постоянная Планка. Своеобразие описания микромира в том, что произведение неопределенности положения Δx и неопределенности импульса Δp_x всегда должно быть равно или больше константы, равной – h/2. Из этого следует, что уменьшение одной из этих величин должно приводить к увеличению другой.

Для других сопряженных величин – энергии E и времени t соотношения неопределенностей, имеет вид: . Это означает, что при характерном времени эволюции системы Δt , погрешность определения ее энергии не может быть меньше чем . Из этого соотношения следует возможность возникновения из ничего, так называемых, виртуальных частиц на промежуток времени меньший, чем и обладающих энергией ΔE. При этом закон сохранения энергии не будет нарушен. Поэтому по современным представлениям вакуум это не пустота, в которой отсутствуют поля и частицы, а физическая сущность, в которой постоянно возникают и исчезают виртуальные частицы.

Одним из основных принципов квантовой механики является принцип неопределенностей. Получение информации об одних величинах, описывающих микрообъект, неизбежно ведет к уменьшению информации о других величинах, дополнительных к первым. микромира необходимо использование, двух противоположных, но дополняющих друг друга представлений.

Вопрос 25. Вопрос 1. Полупроводники. Типы проводимостей и структура энергетических зон

1)Полупроводни́к — материал, который по своей удельной проводимости занимает промежуточное место между проводниками и диэлектриками и отличается от проводников сильной зависимостью удельной проводимости от концентрации примесей, температуры и воздействия различных видов излучения. Основным свойством полупроводника является увеличение электрической проводимости с ростом температуры. Проводимость полупроводников сильно зависит от температуры. Вблизи температуры абсолютного нуля полупроводники имеют свойства диэлектриков.

Энергетические зоны. Между зоной проводимости Е_п и валентной зоной Е_в расположена зона запрещённых значений энергии электронов Е_з. Разность Е_п−Е_в равна ширине запрещенной зоны Е_з. С ростом ширины Е_з число электронно-дырочных пар и проводимость собственного полупроводника уменьшается, а удельное сопротивление возрастает.