Согласные направления токов в индуктивно связанных катушках; одноимённые зажимы индуктивно связанных катушек.

Если линии магнитной индукции одной катушки индуктивности пересекают витки другой катушки то эта катушка имеет индуктивную связь со второй катушкой. На рисунке 1 изображены три индуктивно связанных катушки L1, L2 и L3 с общим магнитопроводом, направления токов каждой катушки известны. 

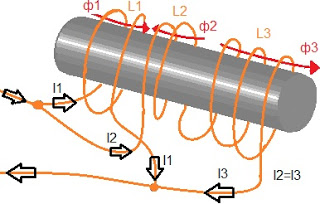
Рисунок 1 - Индуктивно связанные катушки.

Для того чтобы обозначить такое соединение катушек на принципиальной схеме необходимо определить: 1) как катушки соединены друг с другом, 2) направления магнитных потоков каждой катушки. Из рисунка 1 видно что катушка L2 соединена последовательно с катушкой L3 и это соединение соединено параллельно с катушкой L1. Чтобы определить направление магнитного потока катушки можно мысленно обхватить катушку правой рукой так чтобы мизинец, безымянный палец, указательнай палец и средний палец указывали направление тока в её витках и направить большой палец на 90^o  в сорону он (большой палец) укажет направление магнитного потока. Если в индуктивно связанных катушках потоки направлены в одну сторону то их соединение называют согласным, если в индуктивно связанных катушках потоки направлены в разные стороны то их соединение называют встречным. После того как на принципиальной схеме обозначены катушки и направления токов в них около катушек ставят точки так чтобы было видно какие из катушек с какими соединены встречно а какие с какими согласно. Если ток одной катушки входит в её сторону с точкой и ток другой катушки входит в её сторону с точкой то эти катушки соединены согласно.  Если ток одной катушки входит в её сторону без точки и ток другой катушки входит в её сторону без точки то эти катушки соединены согласно.  Если ток одной катушки входит в её сторону с точкой а ток другой катушки входит в её сторону без точки то эти катушки соединены встречно. Учитывая это по рисунку 1 можно составить схему:

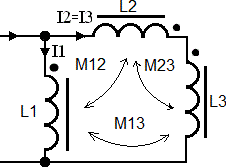
Рисунок 2 - Принципиальная схема с индуктивно связанными катушками.

В получившейся схеме, на рисунке 2, соединены согласно катушки L1 и L3, соединены встречно катушки L2 и L3 и катушки L1 и L2.

11. Коэффициенты взаимной индукции и индуктивной связи.

Электрическая цепь, содержащая взаимные индуктивности, может быть упрощена, если воспользоваться приемом, который называется устранение или развязка индуктивных связей. Им можно воспользоваться только, если катушки присоединены к общему узлу. Возможно два случая: катушки соединены одноименными выводами или разноименными выводами.

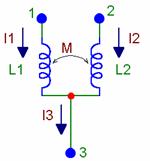
Рисунок 4.4 - Присоединение катушек с взаимной индуктивностью присоединенных к общему узлу

;   ;

.

Верхние знаки - когда одноименные соединены. Нижние - когда разноименные.

Исключаем из первого уравнения I₂, а из второго I₁:

;

;

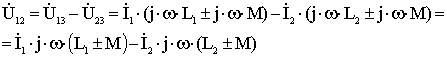
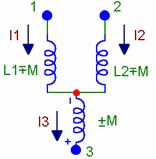
Рисунок 4.5 - Эквивалентная схема замещения для катушек с взаимной индуктивностью, присоединенных к общему узлу

Уравнения и схема замещения трансформатора без ферромагнитного сердечника

Трансформатор представляет собой аппарат, передающий энергию из одной цепи в другую посредством электромагнитной индукции. Он применяется для различных целей, но чаще всего предназначается для преобразования величин переменных напряжений и токов. Трансформатор состоит из двух или нескольких индуктивно связанных обмоток, насаженных на общий сердечник.

На рис. 3.8 активные сопротивления обмоток условно вынесены и изображены отдельно. Обмотка трансформатора, присоединяемая к источнику питания, называется первичной, а обмотка, к которой подключается нагрузка – вторичной. При заданной полярности зажимов обмоток трансформатора на рис. 3.8 токи направлены встречно, что не имеет принципиального значения.

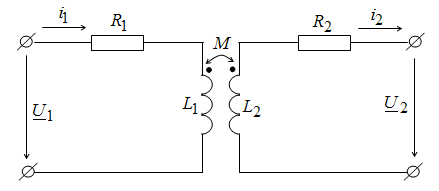
Рис. 3.8. Электрические элементы трансформатора

Уравнения трансформатора в дифференциальной форме:

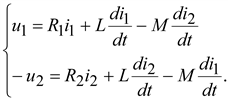 (3.16)

В комплексной форме записи:

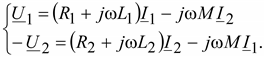 (3.17)

Первичные и вторичные обмотки имеют магнитную связь. На практике при расчетах удобнее заменить эту магнитную связь на электрическую.

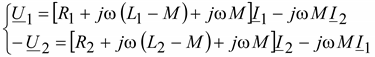.(3.18)

Последние уравнения являются контурными для следующей схемы (рис. 3.8).

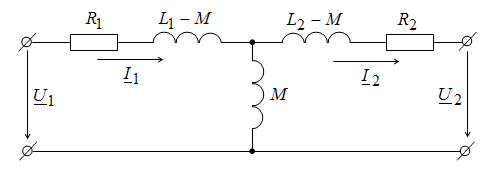
Рис. 3.8. Схема замещения трансформатора

Эта схема может рассматриваться в качестве схемы замещения трансформатора без ферромагнитного сердечника. В схеме замещения, в отличие от предыдущей, первичная и вторичная цепи трансформатора связаны не индуктивно, а электрически. Входящие в эту схему разности L₁ – M и L₂ – M имеют физический смысл только при одинаковом числе витков W₁ и W₂. В этом случае они представляют собой индуктивности рассеяния L_s1 и L_s2 обмоток трансформатора.

Для изображения таким образом трансформатора с разным чисел витков обмоток осуществляют приведение трансформатора. Приведение заключается в том, что напряжение U₂ и ток I₂ заменяются величинами, приведенными к первичной обмотке: напряжение U₂ умножается на n, а ток I₂ делится на n, где n = W₁/W₂ – отношение чисел витков, называемое коэффициентом трансформации. Внесем изменения в (3.17)

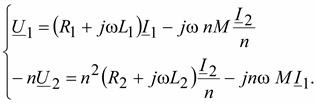 (3.19)

Схема замещения приведенного трансформатора представлена на рис. 3.9.

Уравнения (3.19) можно преобразовать к такому виду, чтобы они стали контурными для схемы на рис. 3.9:

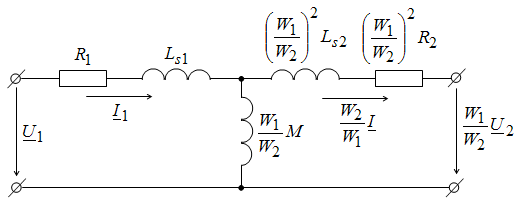
Рис. 3.9. Схема замещения приведенного трансформатора

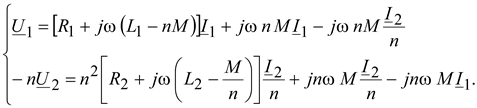 (3.20)

Приведенная схема замещения трансформатора содержит индуктивность 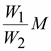  в поперечной ветви, которую называют ветвью намагничивания. Намагничивающая сила, определяющая общий магнитный поток, который пронизывает обмотки W₁ и W₂, при встречном направлении токов равна

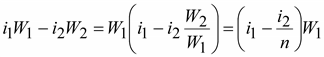. (3.21)

Ток 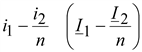 , проходящий через ветвь намагничивания, называется намагничивающим током трансформатора. Построим векторную диаграмму приведенного трансформатора (рис. 3.10).

При построении диаграммы в качестве исходного вектора принят приведенный вторичный ток. Падение напряжения от приведенного вторичного тока I₂/n в приведенном вторичном сопротивлении R₂n² и индуктивном сопротивлении рассеяния ωL_s2 n² вторичной обмотки складываются с приведенным вторичным напряжением nU₂, которое опережает ток I₀/n на угол φ₂. Полученное напряжение равно падению напряжения в индуктивном сопротивлении ветви намагничивания jωnM(I₁ – I₂/n). Ток намагничивания отстает от напряжения на угол 90⁰. Первичный ток находится как геометрическая сумма токов I₂/n и (I₁ – I₂/n). Падения напряжения от тока I₁ в R₁ и ωL_s1 геометрически складываются с напряжением на ветви намагничивания, образуя первичное напряжение.

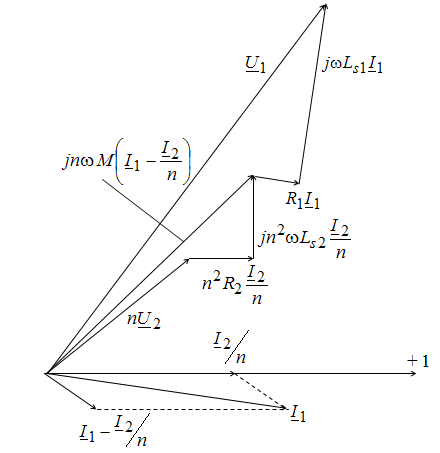
Рис. 3.10. Векторная диаграмма приведенного трансформатора

Так как вторичные электрические величины U₂ и I₂ в последней схеме приведены к первичной обмотке, то данная схема приведенного трансформатора не эквивалентна исходной. Эквивалентной будет так называемая схема идеального трансформатора, у которого при любых условиях отношение U₁/U₂ равно отношению I₂/I₁ = n. Идеальный трансформатор не имеет потерь энергии и при разомкнутой вторичной обмотке ток через его первичную обмотку не проходит. Реально таких трансформаторов нет, но по свойствам к нему близок трансформатор с коэффициентом связи примерно равным единице и со столь большим числом витков, что сопротивление   практически равно бесконечности.