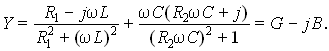- •Уравнение для потенциала в узлах
- •Практическое применение [править]Составление системы уравнений
- •[Править]Пример системы уравнений
- •Описание явления
- •[Править]Замечания
- •[Править]Применение
- •Комплексная форма записи мощности
- •Условие передачи максимальной мощности от источника энергии к приёмнику
- •Последовательный колебательный контур
- •Окончательно запишем , (2.4)
- •Итак (2.6)
- •Описание явления
- •[Править]Замечания
- •[Править]Применение
- •Полоса пропускания колебательного контура
- •Согласные направления токов в индуктивно связанных катушках; одноимённые зажимы индуктивно связанных катушек.
- •Коэффициенты взаимной индукции и индуктивной связи.
- •Входное и вносимое сопротивления трансформатора.
- •Принужденная и свободная составляющие переходного процесса. Классический метод расчета
- •Пример применения операторных методов
- •[Править]Задача
- •Решение операторным методом
- •[Править]Вывод
- •[Править]Замечания
- •Определение [править]Прямое преобразование Лапласа
- •[Править]Обратное преобразование Лапласа
[Править]Применение
Высокодобротный колебательный контур оказывает току определенной частоты f значительное сопротивление. Вследствие чего явление резонанса токов используется в полосовых фильтрах как электрическая «пробка», задерживающая определенную частоту.
Так как току с частотой f оказывается значительное сопротивление, то и падение напряжения на контуре при частоте f будет максимальным. Это свойство контура получило название избирательность, оно используется в радиоприемниках для выделения сигнала конкретной радиостанции.
Колебательный контур, работающий в режиме резонанса токов, является одним из основных узлов электронных генераторов.
Частотные характеристики напряжения на параллельном колебательном контуре Двухполюсные цепи, содержащие индуктивности и емкости, реактивные сопротивления которых имеют противоположные знаки, обладают специфическими частотными свойствами. При определенных частотах в таких цепях может наблюдаться полная компенсация реактивного сопротивления (X = 0), входное сопротивление принимает чисто активный характер, напряжение и ток на входе цепи совпадают по фазе ( = 0) — в цепи наблюдается резонанс. В резонансных режимах токи и напряжения на отдельных участках цепи могут существенно превышать входные величины. Как будет показано далее, это позволяет выделять резонансные частоты из спектра колебаний сложной формы, однако в ряде случаев возникновение резонансного режима может вызвать и нежелательные последствия: перегрузку или повреждение элементов цепи при появлении больших токов и напряжений.
Для определения резонансных частот двухполюсной цепи используется равенство нулю ее эквивалентного реактивного сопротивления или проводимости X = 0, B = 0.
Решение этих уравнений относительно частоты приводит к определению резонансных частот 0. Для цепей, включающих элементы R, L, C, оба указанных условия эквивалентны, так как эквивалентные реактивные параметры двухполюсника связаны соотношениемB = X/(R2 + X2). Для цепей без потерь, составленных только из индуктивностей и емкостей, при нулевом эквивалентном активном сопротивлении имеем B = 1/X, и оба условия дают различные значения резонансных частот. В таких цепях при условии X = 0 при резонансе обращается в нуль напряжение на входе цепи, а при B = 0 равен нулю входной ток двухполюсника. Существование таких режимов возможно, так как в цепи без потерь протекание токов в отдельных ветвях не сопровождается потерями энергии в цепи, на преодоление которых требовалось бы потребление активной мощности от источника.
Рассмотрим частотные свойства простейших цепей с последовательным или параллельным соединением индуктивности и емкости — колебательных контуров.
Комплексное
входное сопротивление последовательного
колебательного контура (рис.
8.7) равно 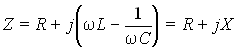 ,
его полное сопротивление
,
его полное сопротивление ![]() .
.
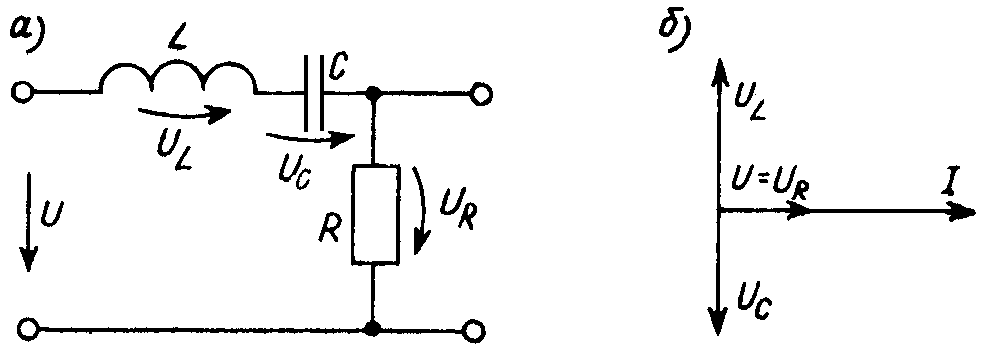
Рис. 8.7
Частотная зависимость z() имеет минимум при условии X = L – 1/C = 0 на резонансной частоте ω0 = 1/LC.
В режиме резонанса Z = R и, несмотря на присутствие реактивных элементов, ток в цепи совпадает по фазе с входным напряжением ( = 0).
Проанализируем частотные зависимости X() и z(). При 0 полное сопротивление цепи неограниченно возрастает за счет роста емкостного сопротивления 1/C, при неограниченно возрастает индуктивное сопротивление, и z (рис. 8.8).
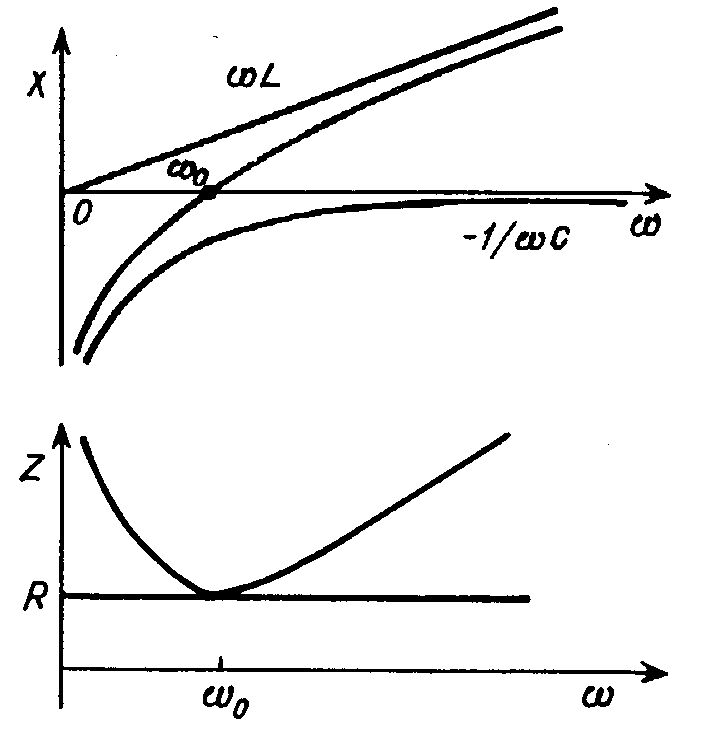
Рис. 8.8
Частотные зависимости тока в цепи и напряжений на ее элементах выражаются формулами:
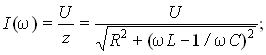
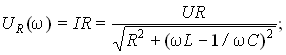
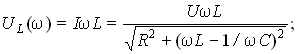
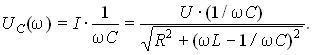
Вид их частотных характеристик (рис. 8.9) определяется характером частотной зависимости z(). Зависимости I и U имеют максимум на резонансной частоте 0
![]()
При 0 и ток в цепи и напряжение на резисторе убывают до нуля.
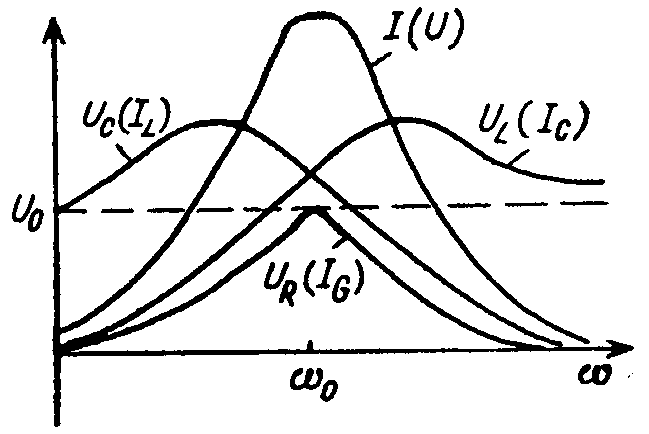
Рис. 8.9
Напряжение UC при = 0 равно входному напряжению U, так как конденсатор в этом режиме представляет разрыв в цепи. При напряжение UC убывает за счет спада тока и сопротивления 1/C. Зависимость UC() может иметь максимум в окрестности резонанса (рис. 8.9). При определенных соотношениях между параметрами контура возможен монотонный спад кривой UC().
Напряжение UL, равное нулю при = 0, затем возрастает, либо достигая максимума в окрестности резонанса (рис. 8.9), либо монотонно приближаясь к напряжению U при , когда сопротивление L неограниченно растет и индуктивность эквивалентна разрыву в цепи.
На резонансной частоте оба напряжения UC0 и UL0 равны и, полностью компенсируют друг друга (см. векторную диаграмму на рис. 8.7, б):
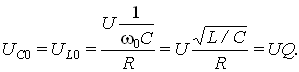
Величина 0L/R = 1/(0CR) = L/C/R = Q — добротность контура,
показывает, во сколько раз напряжения
на реактивных элементах UC0
и UL0
при резонансе превосходят напряжение
источника U.
Эта величина определяет также и характер
кривых UC()
и UL().
Монотонный характер этих зависимостей
наблюдается при ![]() .
Обратная величина d = 1/Q —
это затухание контура.
.
Обратная величина d = 1/Q —
это затухание контура.
Рассматривая UR в качестве выходного напряжения цепи, проанализируем характер зависимости UR() в окрестности резонансной частоты .
Рис. 8.10 |
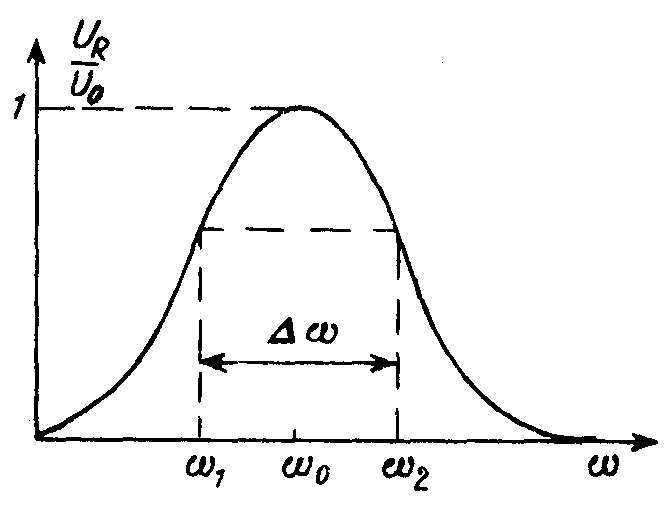
Передаточная функция K() = UR/U0 =
имеет при резонансе максимум, равный единице. Найдем значения частот 1 и 2, при которых значение K() уменьшается до 1 /2(рис. 8.10). При этих частотах значение подкоренного выражения, увеличивается вдвое по сравнению со своим значением при резонансе, равным R2. Это дает условия для определения частот 1 и 2:
|
Отсюда имеем:
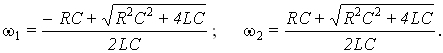
Разность 2 – 1 — полоса пропускания цепи — определяет диапазон частот, в котором отличие сигнала на выходе цепи от своего максимального значения не превосходит 2. При использовании логарифмических единиц это соответствует 3 дБ. Для мощности P, являющейся квадратичной функцией напряжения, отношение P/Pmax на границах полосы пропускания при частотах 1 и 2 составляет 1/2.
Подобное понятие вводится не только для колебательного контура, но и для произвольной цепи, в которой в качестве полосы пропускания принимают диапазон частот, в котором активная мощность, выделяемая в нагрузке, составляет не менее половины от своего максимального значения, или напряжение на нагрузке Uн > Uн max/Хотя понятие полосы пропускания является условным, оно отражает избирательный характер передачи сигнала от источника к нагрузке.
Используя полученные выражения для 1 и 2, для полосы пропускания контура найдем = 2 – 1 = R/L. Отношение резонансной частоты 0 к равно добротности контура: 0/ L/(RLC) = L/C/R = Q. Таким образом, у резонансного контура с более высокой добротностью, относительная ширина полосы пропускания /0 ýже. Это свойство колебательных контуров используют на практике для выделения сигнала данной частоты из совокупности различных частот.
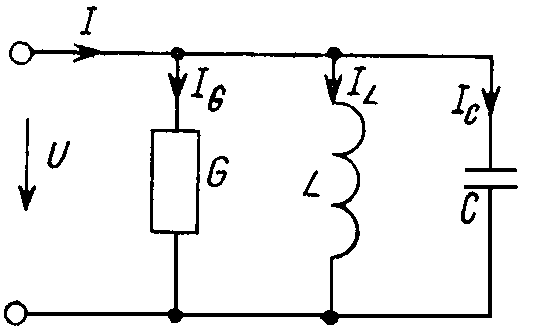
Контур с параллельным соединением G, L, C (рис. 8.11) дуален последовательному контуру.
Рис. 8.11 |
Поэтому
изучать его свойства будем с
использованием аналогии, вытекающей
из принципа
дуальности.
Так, частотная зависимость полной
проводимости контура |
У контура с высокой добротностью Q = C/L/G этот спад имеет резкий характер, для идеального контура с G = 0 имеем z(0) = .
При питании параллельного контура от источника тока I = const частотные зависимости U, IG, IL и IC (обозначения в скобках на рис. 8.9) тождественны изображенным на рис. 8.9 кривым I, UR, UC и UL. При частотах, близких к резонансной, ток в параллельных ветвях L и Cвысокодобротного контура значительно превышают ток входной ветви I; отношение IL0/I = IC0/I = Q.
Анализ работы контура при питании от источника напряжения U приводит к элементарным результатам: IG = UG; IL = U/L; IC = UC. Зависимости токов в ветвях контура от частоты имеют очевидный характер. Для общего тока имеем в этом случае I = Uy. Эта зависимость подобна кривой z() (рис. 8.8).
Рассмотренные свойства последовательного и параллельного колебательных контуров показывают, что подобные двухполюсники удобно использовать для фильтрации сигналов — подавления или выделения определенных частот путем настройки контура на эту частоту в качестве резонансной. При высокой добротности полное сопротивление последовательного контура, малое при частотах, близких к резонансной, резко возрастает при удалении от нее. Сопротивление высокодобротного параллельного контура, наоборот, весьма велико при резонансной и близких к ней частотах, и резко падает при удалении от резонансной частоты. Это позволяет осуществить ограничение сигнала данной частоты путем включения параллельных LC-звеньев последовательно в цепь прохождения тока к нагрузке и последовательных LC-цепочек параллельно сопротивлению нагрузки (рис. 8.12, а).
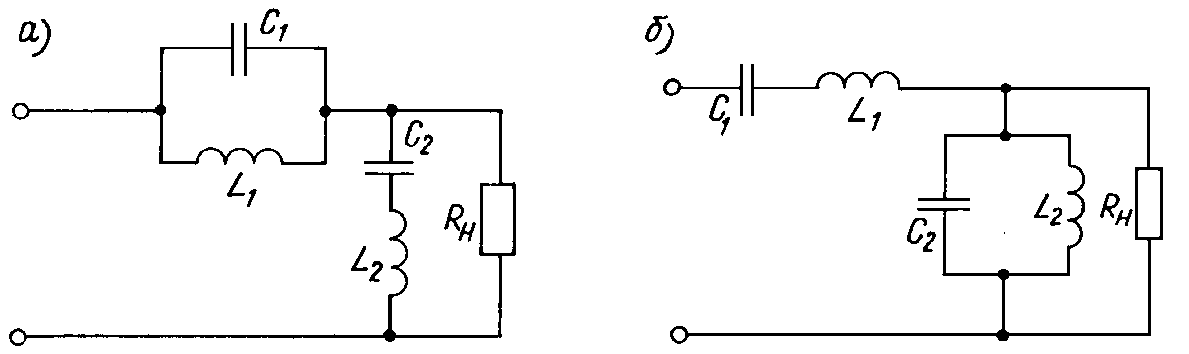
Рис. 8.12
При
соблюдении условий ![]() в
сопротивлении Rн ток
частоты 0 будет
отсутствовать.
в
сопротивлении Rн ток
частоты 0 будет
отсутствовать.
Для решения противоположной задачи — выделения сигнала с частотой0 из спектра частот — последовательные и параллельные контуры следует включить противоположным образом (рис. 8.12, б). Настройка обоих контуров на частоту 0 приводит к тому, что все сигналы, частота которых отличается от данной, будут ослабляться подобным фильтром.
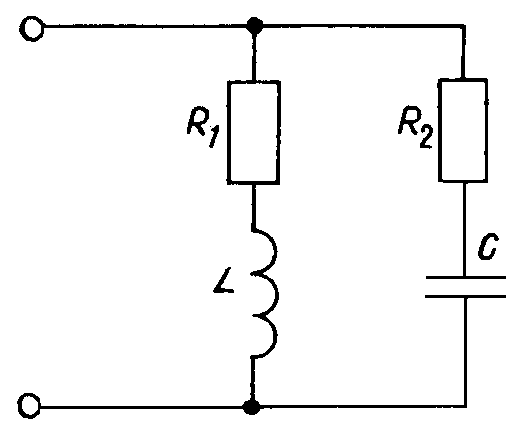
Параллельный колебательный контур с потерями (рис. 8.13).
Рис. 8.13 |
Оценим,
насколько зависят частотные свойства
идеального параллельного LC-контура
от потерь энергии в активных
сопротивлениях элементов контура R1 и R2.
Для определения резонансной частоты
используем выражение комплексной
проводимости контура
|
Его
мнимая часть определяет реактивную
проводимость 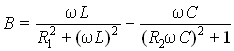 .
Из условия B = 0
найдем
.
Из условия B = 0
найдем 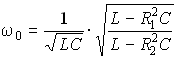 .
Отсюда следует, что при больших
значениях R1 или R2,
когда подкоренная дробь становится
отрицательной, резонанс в цепи отсутствует.
Это характерно для цепей с резистивными
элементами, в которых наличие катушек
и конденсаторов не гарантирует
возникновения резонансного режима. В
отличие от параллельного контура без
потерь (R1 = R2 = 0),
обладающего нулевой входной проводимостью
на резонансной частоте, контур с потерями
имеет ненулевую проводимость при
резонансе, так как протекание тока в
параллельных ветвях сопровождается
потерями, которые должны покрываться
источником во входной ветви.
.
Отсюда следует, что при больших
значениях R1 или R2,
когда подкоренная дробь становится
отрицательной, резонанс в цепи отсутствует.
Это характерно для цепей с резистивными
элементами, в которых наличие катушек
и конденсаторов не гарантирует
возникновения резонансного режима. В
отличие от параллельного контура без
потерь (R1 = R2 = 0),
обладающего нулевой входной проводимостью
на резонансной частоте, контур с потерями
имеет ненулевую проводимость при
резонансе, так как протекание тока в
параллельных ветвях сопровождается
потерями, которые должны покрываться
источником во входной ветви.
В
остальном частотная зависимость y() контура
с потерями при высокой добротности ![]() близка
к частотной характеристике проводимости
контура без потерь y() = 1/(L) – C, отличаясь
от последней тем, что проводимость
контура с потерями сохраняет конечное
значение при нулевой и бесконечно
большой частотах.
близка
к частотной характеристике проводимости
контура без потерь y() = 1/(L) – C, отличаясь
от последней тем, что проводимость
контура с потерями сохраняет конечное
значение при нулевой и бесконечно
большой частотах.
Наибольший
практический интерес рассматриваемая
цепь представляет при R2 = 0,
поскольку активное сопротивление
катушки существенно превышает активное
сопротивление конденсатора. В этом
случае резонансная частота равна ![]() ,
а проводимость контура при
резонансе y() = R1C/L.
При высокой добротности эта величина
достаточно мала, что позволяет использовать
подобный контур для эффективного
подавления нежелательных частот в
рассмотренных выше схемах фильтрации
сигналов (см. рис. 8.12).
,
а проводимость контура при
резонансе y() = R1C/L.
При высокой добротности эта величина
достаточно мала, что позволяет использовать
подобный контур для эффективного
подавления нежелательных частот в
рассмотренных выше схемах фильтрации
сигналов (см. рис. 8.12).
Метод компле́ксных амплитуд — метод расчета линейных электрических цепей, содержащих реактивные элементы, в установившемся режиме при гармонических входных сигналах, впервые применённый О. Хевисайдом.
Суть метода заключается в следующем:
Для всех реактивных элементов определяется их комплексный импеданс.
Все токи и напряжения рассматриваются в виде комплексных амплитуд.
После введения этих замен задача анализа цепи сводится к задаче анализа цепи на постоянном токе:
импедансы трактуются как обычные сопротивления
комплексные амплитуды токов и напряжений как обычные токи и напряжения
Таким образом, мы избавились от реактивности элементов и зависимости от времени сигналов. Эти факторы, затрудняющие математическое описание схемы, теперь перенесены в сигнал: все параметры зависят от частоты гармонического сигнала и являются комплекснозначными.
Задача анализа цепи на постоянном токе решается соответствующими методами, например, методом узловых потенциалов или методом контурных токов. После нахождения всех искомых комплексных амплитуд их можно при необходимости перевести обратно в гармонические сигналы.
Мощность в цепи гармонического тока
Энергетические
процессы в цепях переменного тока
являются функциями времени. Рассмотрим
мощности отдельных участков цепи с
последовательным соединением R, L, C (рис.
2.15), для чего допустим, что к ней приложено
напряжение![]() и
протекает ток
и
протекает ток ![]() .
.
Мощность в активном сопротивлении
![]() .
.
Учитывая RI = UR, а также равенство UR = Ucosφ, полученное из треугольника напряжений, будем иметь
![]() .
.
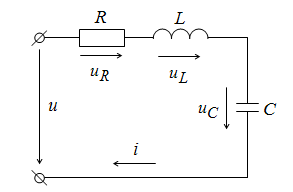
Рис. 2.15. Схема последовательной цепи
Из этого выражения видно:
1) мгновенная мощность в активном сопротивлении всегда положительна (т.е. всегда потребляется);
2) мгновенная мощность колеблется с двойной частотой около своего среднего значения, равного U I cos φ.
Кривая изменения мощности на активном сопротивлении показана на рис. 2.16.
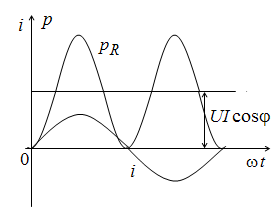
Рис. 2.16. Мгновенная мощность на активном сопротивлении
Мощность в индуктивности
![]() .
.
Но ![]() ,
следовательно,
,
следовательно, ![]() .
Кривые тока и мощности показаны на рис.
2.17.
.
Кривые тока и мощности показаны на рис.
2.17.
Из полученного выражения видно, что мгновенная мощность в индуктивности колеблется с двойной частотой около своего нулевого значения. Следовательно, каждые четверть периода энергия поступает в магнитное поле катушки, чтобы в последующие четверть периода вернуться полностью в источник питания, т.е. идеальная катушка индуктивности энергии не потребляет.
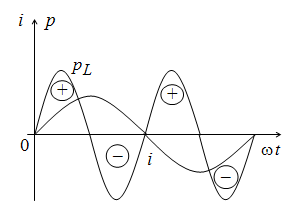
Рис. 2.17. Кривые тока и мощности на индуктивности
Мощность в емкости
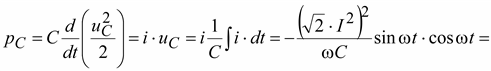
![]() .
.
Кривые тока и мощности показаны на рис. 2.18.
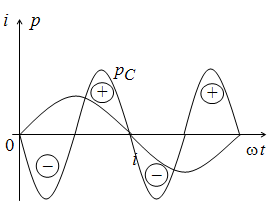
Рис. 2.18. Кривые тока и мощности на емкости
Эти выражения показывают, что в конденсаторе емкостью С энергия не потребляется. Так же, как и в индуктивности, она колеблется около нулевого значения с двойной частотой, поступая от источника и возвращаясь к нему. Следует отметить, что мощности в индуктивности и в емкости колеблются в противофазе. Это говорит о том, что магнитное и электрическое поле способны обмениваться запасами энергии друг с другом.
В соответствии с этим суммарная мгновенная мощность, накапливаемая в индуктивности и емкости, будет равна
![]()
![]() .
.
Этой мощностью, называемой мгновенной реактивной мощностью, реактивные элементы обмениваются не между собой, а с источником питания.
При ![]() ,
т.е. в режиме резонанса напряжений, эта
реактивная мощность равна нулю и катушка
и конденсатор обмениваются энергией
только между собой, на получая ничего
от источника и не возвращая в него.
,
т.е. в режиме резонанса напряжений, эта
реактивная мощность равна нулю и катушка
и конденсатор обмениваются энергией
только между собой, на получая ничего
от источника и не возвращая в него.
Определим мгновенную полную мощность.
Если к участку цепи приложено напряжение u = Um×sin(ω×t + φ) и по нему протекает ток i = Im×sin ω×t, то мгновенная мощность, поступающая в цепь, будет равна
![]() .
(2.34)
.
(2.34)
Она
состоит из двух слагающих: постоянной
величины ![]() ,
равной постоянной составляющей мгновенной
мощности активного сопротивления, и
гармонической, имеющей двойную частоту.
,
равной постоянной составляющей мгновенной
мощности активного сопротивления, и
гармонической, имеющей двойную частоту.
Средняя мощность
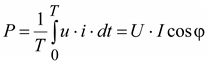 .
.
Эта мощность выделяется в приемниках электрической энергии. Множитель cos φ носит наименование коэффициента мощности.
![]() ;
;
![]() .
.
Согласно (2.34) мгновенная мощность колеблется с двойной частотой 2ω относительно средней мощности P = U I cos φ.
На рис. 2.19 показаны кривые изменения во времени тока, напряжения и мощности цепи.
Когда ток и напряжение имеют одинаковый знак, мгновенная мощность положительна, и энергия поступает от источника к приемнику, где преобразуется в тепло (на активном сопротивлении) и запасается в магнитном поле катушки индуктивности или в электрическом поле конденсатора. Когда ток и напряжение имеют разные знаки, мгновенная мощность отрицательна, и энергия возвращается от приемника к источнику.
На практике пользуются понятиями активной, реактивной и полной мощности.
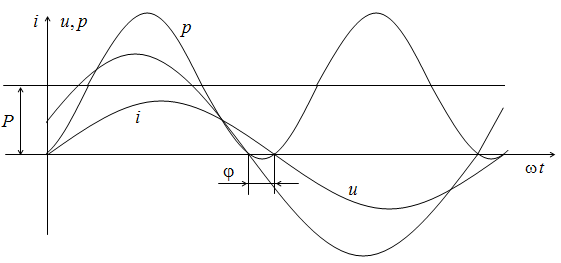
Рис. 2.19. Кривые изменения тока, напряжения и мощности
Под активной мощностью понимают среднее значение полной мгновенной мощности за период
P = U I cos φ.
Активная мощность никогда не бывает отрицательной, так как ею характеризуется потребление энергии цепью. Единицей измерения активной мощности принят ватт (Вт).
Реактивная мощность (Q) характеризует ту часть энергии, которой цепь обменивается с источником без потребления. Ее величина определяется амплитудным значением мгновенной реактивной мощности, выражение которой было ранее получено в виде U I sinφ sin 2ωt. Следовательно,
Q = U I sin φ.
Реактивную мощность принято измерять в вольт-амперах реактивных (ВАр). Она положительна при отстающем токе (когда φ > 0) и отрицательна при опережающем (когда φ < 0).
Полезная работа, совершаемая элементами цепи, характеризуется активной мощностью P. Однако эта мощность зависит от угла сдвига фаз φ, значение которого может меняться в зависимости от режима работы цепи. Следовательно, активная мощность не может быть той расчетной величиной, на которую можно приводить расчет электрических машин, аппаратов и других устройств. Поэтому их характеризуют полной мощностью
S = U×I,
являющейся произведением действующих значений тока и напряжения. Полная мощность равна наибольшему значению активной мощности, которую можно получить при заданных токе и напряжении. Единицей измерения полной мощности принят вольт-ампер (ВА).
Активная, реактивная и полная мощности связаны между собой соотношениями прямоугольного треугольника, называемого треугольником мощностей (рис. 2.20):
![]() ;
;
![]()
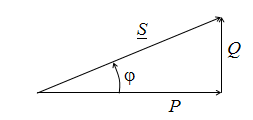
Рис. 2.20. Треугольник мощностей
Необходимо обратить внимание на особенности в понимании активной, реактивной и полной мощностей.
Активная мощность определяет ту работу, которая в среднем совершается (передается) в электрической цепи. Полная и реактивная мощности не определяют ни совершаемой работы, ни передаваемой энергии. Полная мощность, часто называемая кажущейся, является пределом, которого следует добиваться в целях повышения КПД. Реактивная мощность является условной величиной, характеризующей энергию электрических и магнитных полей, имеющихся в цепи.
Запишем мощность в комплексной форме
Символическое
представление действующих значений
тока I и напряжения U позволяет легко и
просто найти активную реактивную и
полную мощности. Для этого необходимо
взять произведение комплексного
напряжения U и комплекса ![]() ,
сопряженного с комплексным током I
,
сопряженного с комплексным током I
![]()
![]()
![]()
![]() .
.
Из этого выражения видно, что вещественная часть комплексной мощности равна активной мощности, мнимая часть – реактивной. Модуль комплексной мощности S равен полной мощности S.
![]() ;
; ![]() ;
;
![]() ;
;
![]() .
.

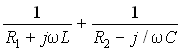 ,
или
,
или