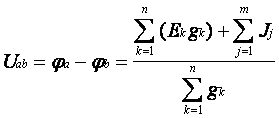Расчет электрических цепей с применением законов Кирхгофа и Ома Законы Кирхгофа наиболее общие. Они являются отдельным случаем универсальных уравнений электрического поля относительно произвольных электрических цепей с сосредоточенными параметрами. Закон Ома используется для расчета только линейных цепей. Алгоритм расчета: 1. Начертить по принципиальной схеме схему замещения; упростить схему, преобразовав последовательно и параллельно соединенные резисторы в эквивалентные, пронумеровать ЭДС соответствующих ветвей, узлы; произвольно выбрать и обозначить положительные направления токов в ветвях. 2. Записать n – 1 уравнений по первому и m – (n – 1) уравнений по второму закону Кирхгофа, где n – количество узлов, m – количество ветвей в цепи. Если бы мы записывали n уравнений по первому закону Кирхгофа, то одно из них – это линейная комбинация оставшихся, что привело бы к линейной зависимости уравнений. Источник тока J входит только в уравнение первого закона Кирхгофа (баланс тока в узлах) и переносится как известное в правую часть уравнения. Для схемы (рис. 1) n = 3, m = 4. 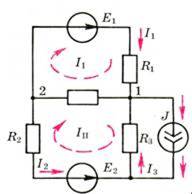Рис. 1.  Ветвь с идеальным источником тока не учитывается, поскольку ее сопротивление бесконечно велико. Уравнение по первому закону Кирхгофа при n – 1 = 2 для узла 1: – I1 – I3 + I4 + J = 0; для узла 2: I1 + I2 – I4 = 0. Уравнение по второму закону Кирхгофа при m – (n – 1) = 4 – 2 = 2 для контура 1 (направление обхода указано пунктиром): I1R1 + I2R2 = E1; для контура 2 (направление обхода то же самое, но можно было взять и противоположное): I2R2 – I3R3 – I4R4 = – E2. 3. Решить систему уравнений относительно тока I: Если среди компонент вектора I есть отрицательные, то это означает, что их направление противоположно положительному направлению, приведенному в схеме (рис. 1). 4. По закону Ома определить напряжения на элементах.  Сложность использования этого метода связана с чрезмерно большой размерностью систем уравнений.

Ме́тод ко́нтурных то́ков — метод сокращения размерности системы уравнений, описывающей электрическую цепь.

Контурные токи – это условно независимые, одинаковые для всех ветвей каждого контура токи (рис.1 , указанные пунктиром II , III), которые совпадают по модулю с соответствующими токами внешних ветвей (например,  ), токи смежных ветвей равняются их сумме (если, направления контурных токов совпадают) или разности (если направления противоположны). Например,  .  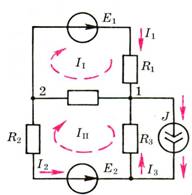 Рис.1. Введение контурных токов дает возможность исключить из системы по первому и второму законам Кирхгофа уравнения первого закона Кирхгофа, снизив размерность системы до m – (n – 1). Для схемы (рис.1) исключим I3 и I4 из двух первых уравнений системы: Из второго уравнения найдем I4, из первого – I3: Подставим полученную формулу в два последних уравнения системы Кирхгофа: Или относительно неизвестных I1 и I2: После введения обозначений (второе уравнение умножили на -1, чтобы III имел дополнительное значение) получим систему уравнений для контурных токов II и III: где R12 = R21 = R4 (взаимное сопротивление Rij будет иметь отрицательное значение, если II и III направлены навстречу друг другу); Е2 также отрицательна, поскольку направление Е2, противоположно по направлению току III, должно быть в левой части уравнения со знаком «-» но после перехода вправо получило знак «+». Обобщим систему для произвольного числа контуров: Элементы   формируются согласно алгоритма метода контурных токов: 1. Выделить m – (n – 1) независимых контуров (каждый новый контур необходимо выбрать так, чтобы в него входил хотя бы один элемент электрической цепи, который не входит в другие контуры: например, для рис. 2, если выбраны контуры abd и bcd, то нельзя брать третьим контур abcd. 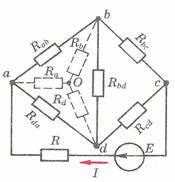  Рис.2. 2. Указать произвольно направления обхода контуров. Если на схеме уже обозначено направление токов в ветвях, то удобно направления контурных токов согласовать с направлением токов в ветвях. 3. Вычислить Rij: Rij равняется сумме сопротивлений всех элементов, входящих в i-й контур; Rij – равняется по модулю сумме сопротивлений ветвей, которые одновременно принадлежат i-му и j-му контурам; Rij больше нуля, если контурные токи i-го контура совпадают по направлению, и меньше нуля – при противоположных направлениях. 4. Вычислить правые части системы: Еi равняется алгебраической сумме ЭДС i-го контура; со знаком «+» берутся ЭДС, внутренняя стрелочка которых совпадает с направлением контурного тока i-го контура, «-» - если не совпадают. Если в семе есть источник тока J, то для его учета необходимо заблаговременно распределить ток J по ветвям любого незамкнутого контура, который дополняет ветвь с источником тока до замкнутого контура (в нашем случае – через R3, однако можно было бы и через R2 и R4). Полученное таким образом произведение J на соответствующее сопротивление необходимо перенести вправо, при этом необходимо поменять знак. 5. Решить систему уравнений относительно I. По контурным токам определить токи в ветвях. Во внешних ветвях они по модулю совпадают, во внутренних совпадающие по направлению складываются, направлены встречно – вычитаются. (В нашем примере I1 = I2; III = - I2; I1 – III = I4; ток I3 определим по первому закону Кирхгофа для узла 3: III – J + I3 = 0, откуда I3 = J - III).

Метод узловы́х потенциалов — метод расчета электрических цепей путём записи системы линейных алгебраических уравнений, в которой неизвестными являются потенциалы в узлах цепи. В результате применения метода определяются потенциалы во всех узлах цепи, а также, при необходимости, токи во всех ветвях.

Введение

Очень часто необходимым этапом при решении самых разных задач электротехники и электроники является расчет электрической цепи. Под этим термином понимается процесс получения полной информации о напряжениях во всех узлах и о токах во всех ветвях заданной электрической цепи. Для расчета линейной цепи достаточно записать необходимое число уравнений, которые базируются на правилах Кирхгофа и законе Ома, а затем решить полученную систему.

Однако на практике записать систему уравнений просто из вида электрической схемы удается только для очень простых схем. Если в схеме более десятка элементов или она содержит много взаимосвязанных контуров (участки типа мостов), то для записи определяющей схему системы уравнений уже требуются специальные методики. К таким методикам относятся метод узловых потенциалов и метод контурных токов.

Метод узловых потенциалов не привносит ничего нового к правилам Кирхгофа и закону Ома. Данный метод лишь формализует их использование настолько, чтобы их можно было применить к любой, сколь угодно сложной цепи и пригоден для расчёта посредством компьютеров. Иными словами, метод даёт ответ на вопрос «как использовать законы для расчета данной цепи?».

Теоретические основы

Если в цепи, состоящей из У узлов и Р рёбер известны все характеристики звеньев (полные сопротивления R, величины источников ЭДС E и тока J), то возможно вычислить токи I_i во всех рёбрах и потенциалы φ_i во всех узлах. Поскольку электрический потенциал определён с точностью до произвольного постоянного слагаемого, то потенциал в одном из узлов (назовём его базовым узлом) можно принять равным нулю, а потенциалы в остальных узлах определять относительно базового узла. Таким образом, при расчёте цепи имеем У+Р–1 неизвестных переменных: У–1 узловых потенциалов и Р токов в рёбрах.

Не все из указанных переменных независимы. Например, исходя из закона Ома для участка цепи, токи в звеньях полностью определяются потенциалами в узлах:

С другой стороны, токи в рёбрах однозначно определяют распределение потенциала в узлах относительно базового узла:

Таким образом, минимальное число независимых переменных в уравнениях цепи равно либо числу звеньев, либо числу узлов минус 1, в зависимости от того, какое из этих чисел меньше.

При расчёте цепей чаще всего используются уравнения, записываемые исходя из законов Кирхгофа. Система состоит из У–1 уравнений по 1-му закону Кирхгофа (для всех узлов, кроме базового) и К уравнений по 2-му закону Кирхгофа для каждого независимого контура. Независимыми переменными в уравнениях Кирхгофа являются токи звеньев. Поскольку согласно формуле Эйлера для плоского графа число узлов, рёбер и независимых контуров связаны соотношением

или

то число уравнений Кирхгофа равно числу переменных, и система разрешима. Однако число уравнений в системе Кирхгофа избыточно. Одним из методов сокращения числа уравнений является метод узловых потенциалов. Переменными в системе уравнений являются У–1 узловых потенциалов. Уравнения записываются для всех узлов, кроме базового. Уравнения для контуров в системе отсутствуют.

Уравнение для потенциала в узлах

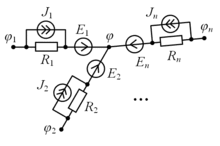
Рис. 1. Фрагмент цепи: узел с примыкающими звеньями

Рассмотрим фрагмент цепи, состоящий из узла и примыкающих к нему звеньев (рис. 1). Согласно 1-му закону Кирхгофа сумма токов в узле равна нулю:

Ток в звене определим исходя из закона Ома для участка цепи:

откуда

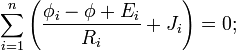
Обозначив проводимости рёбер через

получим окончательное уравнение для узла

Последнее уравнение получено исходя из предположения, что все источники тока и ЭДС направлены в сторону рассматриваемого узла. Если какой-либо источник направлен в противоположную сторону, его ЭДС или ток необходимо взять с обратным знаком.

Записав последнее уравнение для каждого узла цепи кроме базового, получим систему уравнений для узловых потенциалов.

Практическое применение [править]Составление системы уравнений

Перед началом расчёта выбирается один из узлов (базовый узел), потенциал которого считается равным нулю. Затем узлы нумеруются, после чего составляется система уравнений.

Уравнения составляются для каждого узла, кроме базового. Слева от знака равенства записывается:

• потенциал рассматриваемого узла, умноженный на сумму проводимостей ветвей, примыкающих к нему;

• минус потенциалы узлов, примыкающих к данному, умноженные на проводимости ветвей, соединяющих их с данным узлом.

Справа от знака равенства записывается:

• сумма всех источников токов, примыкающих к данному узлу;

• сумма произведений всех ЭДС, примыкающих к данному узлу, на проводимость соответствующего звена.

Если источник направлен в сторону рассматриваемого узла, то он записывается со знаком «+», в противном случае — со знаком «−».

Рис. 2. Пример электрической схемы

[Править]Пример системы уравнений

На схеме (рис. 2) четыре узла. Потенциал в узле 0 принят равным нулю (φ₀ = 0). Записываем уравнения для узлов 1, 2 и 3:

где проводимости рёбер равны

Метод наложения — метод расчёта электрических цепей, основанный на предположении, что ток в каждой из ветвей электрической цепи при всех включённых генераторах, равен сумме токов в этой же ветви, полученных при включении каждого из генераторов по очереди и отключении остальных генераторов(только в линейных цепях).

Метод наложения используется как для расчёта цепей постоянного тока, так и для расчёта цепей переменного тока.

Найти ток   методом наложения в цепи, показанной на рисунке.  ,  ,    .

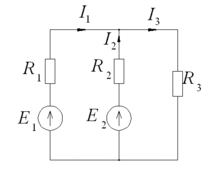
Пример метода наложения

При отключённом генераторе 2 ток   найдём по формуле:

.

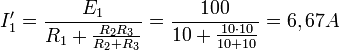При отключённом источнике 1, ток   будет

,

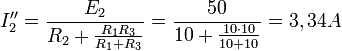а ток   будет

.

Тогда ток   при обоих включённых источниках будет равен сумме токов   и  :

.

В задаче за положительные направления токов   и   приняты направления, совпадающие с направлением, показанным на рисунке для тока  . То же самое для тока 

Теоремы об эквивалентном источнике напряжения и эквивалентном источнике тока.

Курс теории электрических цепей является составной частью курса теоретических основ электротехники (ТОЭ). Это фундаментальная наука, базирующаяся на исследованиях в области электрических и магнитных явлений.

Теорема об эквивалентном источнике (эквивалентном генераторе)

Определения

Автономный двухполюсник – двухполюсник, напряжение холостого хода или ток короткого замыкания которого не равны нулю.

Комплексное входное сопротивление двухполюсника – отношение комплексной амплитуды напряжения на его зажимах к амплитуде тока.

Ток произвольной ветви линейной электрической цепи не изменится, если автономный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным линеаризованным источником энергии, который может быть представлен последовательной или параллельной схемой замещения. Э. д. с. идеального источника напряжения в схеме замещения равна напряжению холостого хода автономного двухполюсника, ток тока равен току короткого замыкания а внутреннее сопротивление и внутренняя проводимость эквивалентного равны соответственно комплексному входному сопротивлению комплексной входной проводимости двухполюсника.

Доказательство. Введем в выделенную ветвь k—k' два вспомогательных независимых источника напряжения>  и  , э. д. с. которых равны по значению, но противоположны по направлению (рис. 8.5, а). Введение двух скомпенсированных источников э. д. с. не нарушает режима работы цепи, поэтому ток ветви k—k' преобразованной цепи равен току исходной цепи. Далее, используя принцип наложения, представим ток рассматриваемой ветви преобразованной цепи в виде суммы двух составляющих:

,

где> —частичный ток k-ой ветви, создаваемый действием независимого источника напряжения   и всех независимых источников, входящих в состав автономного двухполюсника АД, а   — частичный ток k-oй ветви, вызываемый действием независимого источника напряжения  .

Из эквивалентной схемы, изображенной на рис. 8.5, б следует:

,

Выберем  так, что  . Тогда напряжение на внешних зажимах АД равно напряжению холостого хода автономного двухполюсника  Используя выражение (3.11), найдем значение э. д. с.   при котором частичный ток k-ой ветви :

>

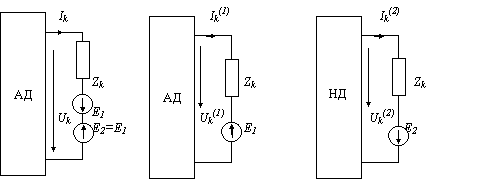
Рис. 8.5. К доказательству теоремы об эквивалентном источнике.

(АД – автономный двухполюсник, НД неавтономный двухполюсник)>

Используя эквивалентную схему (рис. 8.5, в) для определения частичного тока > находим

>

где Zэ — комплексное входное сопротивление исходного автономного двухполюсника, равное комплексному входному сопротивлению приведенного на рис. 8.5, в неавтономного двухполюсника НД. Как видно из выражения (8.2), ток k-ой ветви исходной цепи (рис. а) равен току некоторой цепи, содержащей Zk, источник напряжения >   и комплексное сопротивление Zэ = Zkk . Итак, ток ветви не изменился при замене автономного двухполюсника эквивалентным источником энергии, э. д. с. которого равна напряжению холостого хода автономного двухполюсника, а внутреннее сопротивление – его комплексному входному сопротивлению.

Переходя от последовательной схемы замещения эквивалентного источника к параллельной, можно показать, что значение тока Jэк независимого (см. рис. 8.5, в) равно току короткого замыкания автономного двухполюсника, а внутренняя проводимость Yэ — его комплексной входной проводимости Уэ = l/Zkk.

Воспользовавшись теоремой об эквивалентном источнике, можно найти последовательную или параллельную схемы замещения любого сколь угодно сложного линейного активного двухполюсника. Эта теорема позволяет существенно упростить анализ цепей в тех случаях, когда требуется определить ток напряжение только одной ветви сложной цепи. В связи с тем, что параметры элементов последовательной и параллельной схем двухполюсника легко поддаются измерениям, выполняемым на внешних зажимах, теорему источнике применяют для построения эквивалентных активных двухполюсников по результатам их экспериментального исследования.

Выделим из рассматриваемой цепи ветвь, содержащую сопротивление Z6, и представим остальную часть последовательной схемой замещения (рис. 8.6, а).

Методы анализа цепей, ориентированные на применение средств вычислительной техники Общие представления о программах машинного анализа цепей.

Формирование компонентных уравнений цепи Для составления уравнений электрического равновесия цепи с помощью ЭВМ необходимо формализовать исходные о топологии и параметрах входящих в нее элементов.

Формирование топологических уравнений цепи Топологические свойства цепи полностью определяются ее графом, которому ставятся в соответствие топологические матрицы: матрица узлов А, главных контуров В, матрицу сечений Q и др.

Метод переменных состояния Наличие интегралов в уравнениях электрического равновесия цепи, составленных методами узловых напряжений и контурных токов, значительно затрудняет решение этих уравнений течение длительного времени ограничивало возможности применения данных методов при машинном анализе цепей.

Цепи с индуктивной связью Понятие взаимной индуктивности. Одноимённые зажимы.

Одноименные зажимы При анализе цепей с взаимной индуктивностью возникает задача определить, каким образом (согласно или встречно) по отношению к выбранным условным положительным направлениям токов включены рассматриваемые индуктивные катушки и в соответствие этим какой знак (плюс минус) необходимо использовать выражениях (10.10), (10.11).

Метод двух узлов

Данный метод является частным случаем метода узловых потенциалов для схемы с двумя узлами и произвольным количеством любых ветвей ( активных и пассивных ).

В общем случае включения n+m ветвей между некоторыми узлами a-b напряжение между ними определяется выражением

где (Ek gk) – алгебраическая сумма произведений ЭДС ветвей на проводимости этих ветвей;

(Jj) – алгебраическая сумма токов источников тока ветвей между узлами a и b;

(gk) – сумма проводимостей всех ветвей между узлами a-b.

Резонанс токов — резонанс, происходящий в параллельном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.