Глава 1. Линейные радиотехнические цепи с активными и реактивными элементами § 1. Общие сведения о линейных радиотехнических цепях

Все системы, применяемые на практике, подразделяются на линейные и нелинейные. Любое радиотехническое устройство представляет собой сочетание линейных и нелинейных элементов.

Линейными элементами называются такие элементы, параметры которых не зависят ни от величины протекающего по ним тока, ни от величины приложенного к ним напряжения.

Поскольку параметры линейной системы являются величинами постоянными, то зависимость тока в системе от подводимого к ней напряжения является линейной функцией. Например, если радиотехническая цепь содержит резистор R, к которому подведено напряжение U, то ток в цепи пропорционален приложенному напряжению (рис. 3.1.2):

I = Y · U

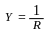
где – электрическая проводимость резистора.

Рис. 3.1.2. Схема и характеристика линейного элемента

Если цепь содержит не только активное сопротивление R, но и реактивные элементы, параметры которых не зависят от тока или напряжения, то и в этом случае ток в цепи также пропорционален приложенному напряжению:

I = Y · U;

г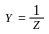 де ; Z – полное сопротивление цепи.

Таким образом, линейные системы характеризуются линейной зависимостью между напряжением и током, т. е. линейной вольтамперной характеристикой.

Оценим поведение линейной системы с сопротивлением Z, если к ее входу приложено напряжение U, являющееся суммой двух синусоидальных колебаний разных частот ω₁ и ω₂ :

U = U_1m · sin ω₁t + U_2m · sin ω₂t ;

Ток, протекающий через сопротивление Z, можно определить из следующих соотношений:

Таким образом, сложение синусоидальных колебаний разных частот в линейной системе не приводит к возникновению новых частот. Поэтому при изучении поведения системы можно рассматривать колебания каждой частоты в отдельности, а затем суммировать полученные результаты.

1.1. Активное сопротивление в цепи переменного тока

Переменный ток представляет собой процесс, при котором напряжение изменяется во времени по синусоидальному закону:

u = U_m · sin ωt;

Ток, протекающий через резистор с сопротивлением R, определяется следующим выражением:

Таким образом, ток, протекающий через активное сопротивление, включенное в цепь переменного тока, совпадает по фазе с приложенным напряжением.

1.2. Индуктивность в цепи переменного тока

Переменный ток, протекающий через индуктивность, описывается следующим выражением:

i = I_m · sin ωt ; ;

П

Ф = Ф_m · sin ωt ;

ри протекании этого тока в катушке индуктивности создается переменный магнитный поток, который совпадает по фазе с протекающим током:

Под воздействием переменного магнитного поля в катушке появляется э.д.с. самоиндукции:

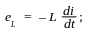
e_L = – ωL · I_m · cos ωt = ωL · I_m · sin (ωt – 90º) ;

Сомножитель ωL имеет размерность сопротивления и представляет собой реактивное сопротивление x_L катушки индуктивности:

x_L = ωL = 2π f L ;

Поэтому ωL · I_m = x_L · I_m = E_m ;

e_L = – E_m · cos ωt = E _m · sin (ωt – 90º) ; ;

Следовательно, э.д.с. самоиндукции отстает по фазе от тока на 90º.

Для поддержания тока в катушке к ней должно быть приложено напряжение u от источника переменного тока, которое в любой момент времени по величине равно э.д.с. самоиндукции, и имеет знак, противоположный знаку э.д.с. самоиндукции:

u = – e_L ;

u = – E _m · sin (ωt – 90º);

После преобразования получаем:

u = U _m · sin (ωt + 90º) ;

Таким образом, напряжение, приложенное к катушке индуктивности, опережает протекающий ток на 90º.

В реальных условиях катушка индуктивности имеет не только реактивное сопротивление ωL, но и активное R. Эквивалентная схема реальной катушки индуктивности приведена на рис. 3.1.3.

Рис. 3.1.3. Эквивалентная схема катушки индуктивности

Векторные диаграммы напряжений и сопротивлений для реальной катушки индуктивности приведены на рис. 3.1.4.

При построении диаграммы напряжений за исходный вектор принят вектор тока I, т. к. его значение одинаково для всей последовательной цепи.

a)

b)

Рис. 3.1.4. Векторные диаграммы катушки индуктивности

a) диаграмма токов и напряжений; b) диаграмма сопротивлений.

Падение напряжения на активном сопротивлении равно:

U_R = I · R ;

Это напряжение совпадает по фазе с протекающим током I. Падение напряжения на индуктивном сопротивлении U_L = I ·  L опережает по фазе ток I на 90º. Суммарное напряжение U является геометрической суммой напряжений U_R и U_L :

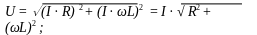
Разделив обе части уравнения на I, получим выражение для общего сопротивления цепи:

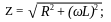
С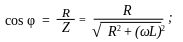 двиг фаз φ между напряжением и током определяется из выражения: