3. Тепе-теңдіктегі күштерді қосу және азайту

Денеге қойылған күштер жүйесіне өзара тепе-теңдіктегі күштер жүйесі қосылса немесе алынса, күштер жүйесінің денеге әсері өзгермейді. Айтайық, дене   күштері әсерінен тепе-теңдікте болсын (1.3-сурет). Денеге және  күштер жүйесін қоялық. Нәтижеде дене жаңа   күштер жүйесі әсерінде де тепе-теңдікте болады, яғни:

Жоғардағы аксиомадан төмендегі теорема келіп шығады.

Теорема: Берілген күшті өзінің әсер сызығы бойымен бір нүктеден екінші нүктеге мөлшері және бағыты өзгертілмей көшірілсе, оның денеге әсері өзгермейді.

4. Әсер және кері әсердің теңдік

Абсолют қатты денелердің бір-біріне әсері тең және олар бір түзу бойымен қарама-қарсы бағытталған, яғни әсер әрқашан кері әсерге тең және оған қарама-қарсы бағыттылған. Бұл аксиома И.Ньютон тарапынан баяндалған болып, ол классикалық механиканың негізгі заңдарының бірі болып есептеледі.

5. Қатты емес денелер тепе-теңдігінің сақталу заңы.

Қатты емес дене күштер әсерінде тепе-теңдікте болса, дене қатты денеге айналғанда да оның тепе-теңдігі өзгермейді. Бұл аксиомадан байқалатыны, абсолют қатты денеге қойылған күштердің тепе-теңдік шарты деформацияланатын денеге қойылған күштер үшін де орынды болады. Мысалы деформацияланатын денелерге тиісті мәселелер қатарына жататын жіп, шынжыр, қайыс, стержень сияқты денелердегі зорығуларды анықтауға тиісті есептер шешуде алтыншы аксиоманы пайдаланамыз.

2. Сұрақ

Гук заңы. Беріктік шарты.

Роберт Гук 1660 жылы тәжірибе жүзінде білеудің абсолют ұзаруы (сығу жағдайында - қысқаруы) мен оған әсер етуші күштің арасында белгілі байланыс барын ашты. Ол білеудің серпімді абсолют ұзаруының білеуге әсер етуші күш пен білеу ұзындығына тура пропорционалдығын, ал қима ауданына кері пропорционалдығын және оның шамасы материалдың қасиетіне де байланыстылығын тапты. Бұл заңдылық Гук заңы деп аталады

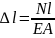
Мұндағы E - материалдың бірінші текті серпімділік модулі, ол тәжірибе жүзінде анықталады. Серпімділік модулі - материал қасиетін сипаттайтын коэффицент; ӛлшем бірлігі кернеудің ӛлшем бірлігіндей.EA – білеудің созылғандағы немесе сығылғандағы қатаңдығы деп аталады, ол материалдың созылуға немесе сығылуға қарсыласу қабілеттігін сипаттайды.

Беріктік деп конструкцияның немесе оның жеке элементтерінің сыртқы күш әсерінен қирамай қарсыласу қабілетін атайды

23- билет

1. Сұрақ

Бұралу кезіндегі беріктік және қатаңдық.

Беріктікдеп конструкцияның немесе оның жеке элементтерінің сыртқы күш әсеріне қирамай қарсыласу қабілетін айтады.

Қатаңдықдеп конструкция мен оның элементтерінің деформацияға қарсыласу қабілетін атайды

2. Сұрақ

Қос күштерді қосу. Қос күштердің тепе-теңдік шарты.

Теорема. Денеге бір жазықтықта әсер ететін қос күштер жиыны, моменті қос күштердің моменттерінің алгебралық қосындысына тең болатын қос күшпен тепе-тең. Сонымен, денеге бір жазықта әсер ететін бірнеше қос күштерді қосу үшін, осы қос күштерінің моменттерінің алгебралық қосындысын анықтаса жеткілікті. Қосу нәтижесінде алынған момент тең әсерлі қос күшті анықтайды,яғни денеге бір жазықта әсер етуші қос күштер жиыныі тепе-теңдікте болу үшін жиындағыі қос күштер моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті.

24- билет

1. Сұрақ

Таралған күштің қарқындылығы, жанама күш, ию моменті арасындағы дифференциалдық байланыс. Жанама күш және ию моменті эпюрлерін тұрғызудың және тексерудің ережелері.

Ию моменті, көлденең күш және бірқалыпты таралған жүктеменің қарқындылығы өзара төменде көрсетілгендей дифференциалдық байланыста болады:

dM/dx=Q; dQ/dx=-q.

Бұл байланыстардың шын мәнінде орын алатындығын көрсету үшін суреттегі арқалықты қарастырып, арқалықтың сол жағындағы тіректен х қашықтықтағы көлденең қимада туындайтын ішкі күштердің өрнегін тұрғызайық.

M(x)=R_A ·x- (q · x²/2), Q(x)=R_A-q ·x.

Енді осы қиманы арқалықтың өсі бойымен шексіз аз dx шамасына жылжытайық, яғни алғашқы қимадан шексіз аз ара қашықтықтағы екінші қиманы қарастырайық. Бұл қимадағы ішкі күштердің шамасы

M(x+dx)=R_A ·(x+dx)-(q·(x+dx)²)/2,

Q(x+dx)=R_A-q·(x+dx).

Жанама күштің өсімшесін анықтайық

dQ=Q(x+dx)-Q(x)=R_A-q ·(q+dx)-R_A+q·x=-q·dx,

екенін көреміз.

Енді ию моментінің өсімшесін анықтайық

dM=M(x+dx)-M(x)=R_A ·(x+dx)-(q(x+dx)²)/2-R_A·x+(qx²)/2.

Бұдан

dM=R_A ·dx-q·xdx=(R_A-q·x)dx=Q·dx

немесе

Q=dM/dx.

Сонымен, мынаны тұжырымдауға болады: бірқалыпты таралған жүктеменің қарқындығы қимадағы көдлденең күш өрнегінің х бойынша алынған теріс таңбалы бірінші туындысына тең; осы қимадағы көлденең күш қимадағы ию моменті өрнегінің х бойынша алынған туындысына тең.