2.Еркін бағытталған жазық. Күштер жүйесінің тепе-теңдік шарты. Кеңістіктегі күштер жүйесі.

Еркін бағытталған жазық күштер жүйесінің тепе-теңдік шарты. Егер еркін бағытталған күштердің бас векторы нқлге тең болса, онда оның модулі де нөлге тең, яғни R=0 болса, онда R= =0 немесе R_x= R_y= .

Осы теңдіктерден тепе-теңдіктің келесі шарттарын аламыз:

1. Еркін бағытталған жазық күштер жүйесінің тепе-теңдікте болуы үшін жүйені құраушы күштерінің екі координат өстеріндегі проекцияларының алгебралық қосындысы және күш жазықтығындағы кез келген бір нүктеге қатысты алынған күштердің моменттерінің алгебралық қосындысы нөлге тең болулары қажет және жеткілікті.

, . Бұл өрнектерді тепе-теңдіктің шарты немесе тепе-теңдік теңдеуі деп атайды.

2. Еркін бағытталған жазық күштер жүйесінің тепе-теңдікте болуы үшін кез келген екі А және В нүктелеріне қатысты құраушы күштерінің моменттерінің алгебралық қосындысы мен АВ түзуіне перпендикуляр болып келмеген қандай да бір өстегі осы күштер проекцияларының алгебралық қосындысы нөлге тең болулары қажет және жеткілікті. , ,

3. Еркін бағытталған жазық күштер жүйесінің тепе-теңдікте болуы үшін жүйенің құрама күштерінің бір түзудің бойында жатпайтын кез келген А, В және С нүктелеріне қатысты моменттерінің алгебралық қосындысы нөлге тең болулары қажет және жеткілікті. , , .

Кеңістіктегі күштер жүйесі. Егер денеге әсер ететін күштердің әсер сызықтары бір жазықтықта жатпайтын болса, күштер жүйесін кеңістіктегі күштер жүйесі деп атайды.

14- билет

1. Сұрақ

Сонымен, «Материалдар кедергісі» деп машина мен конструкциялардың бөліктерінің беріктігі, қатаңдығы және орнықтылығы туралы ғылымды айтамыз.

Беріктік деп конструкцияның немесе оның жеке элементтерінің сыртқы күш әсеріне қирамай қарсыласу қабілетін айтады.

Қатаңдық деп конструкция мен оның элементтерінің деформацияға қарсыласу қабілетін атайды.

Орнықтылық деп конструкцияның немесе оның элементтерінің белгілі алғашқы серпімді тепе-теңдік күйін сақтау қабілетін айтады. Есептеу денелерінің түрлері. Инженерлік практикада кездесетін сан алуан конструкция элементтері пішіндері мен ӛлшемдеріне байланысты жинақталып, тӛмендегідей қарапайым түрлерге жіктелген: 1 Білеу (брус) - екі ӛлшемі үшін,шісінен әлдеқайда кіші дене (I.2.1, а, b - сурет). Дербес жағдайда білеудің кӛлденең қимасының ауданы тұрақты, ал ӛсі түзу сызықты болуы мүмкін (I.2,1, b - сурет).

Ӛсі түзу сызықты білеуді стержень деп атайды. Білеудің өсі дегеніміз кӛлденең қималардың ауырлық центрлерінің геометриялық орны (I.2.1, c - сурет). 2 Пластина – ара қашықтығы басқа ӛлшемдеріне қарағанда ӛте кіші, екі жазық бетпен шектелген дене (I.2.2, а - сурет). 3 Қабықша - ара қашықтығы басқа ӛлшемдеріне қарағанда әлдеқайда кіші болатын екі қисық сызықты беттермен шектелген дене (I.2.2, b - сурет).

Кернеулі күйі деп аталатын,жүктелген стержень материалы жағдайының ең маңызды сипаттамасы болып ішкі күштердің қарқындылығы есептелінеді,яғни серпімді күштердің қима ауданының бірлігіне шаққандағы шамасы қарастырылады. Бұл шама кернеу деп аталады. Материалдың кернеулі күйін зерттеу,яғни жүктелген конструкция элементтерінің кез-келген қимасындағы кернеуді анықтау материалдар кедергісінің ең маңызды есептерінің бірі болып табылады.

Серпімді күштердің таралу заңдылығын зерттеу үшін қима бетіндегі кез- келген нүкте төңірегіндегі,ауданы шексіз кіші dA болатын элементар қиманы бөліп алайық.Осы элементар қимаға түсетін серпімді күштердің тең әсерлі күші dR бас вектор болсын делік. Бас вектор dR-дің шексіз кіші аудан dA-ға қатынасы жүргізілген қиманың берілген нүктесіндегі толық кернеу деп аталады. Формуласы: p= dR / dA

Кернеудің өлшем бірлігі: Н/м²,кН/м²,МН/м²,немесе Па,КПа,МПа. 1 КПа=10 ³Па, 1МПа = 10 ⁶ Па.

Қарастырылған кимадағы берілген нүеткнің кернеуі векторлық шама , ол өзінің бағытымен және шамасымен анықталады.

Тік кернеу σ – осьтік іщкі күштің қарқындығы немесе қарастырылған қиманың берілген нүктесінің аудан бірлігіне келтірілген осьтік күш : σ = dN / dA

Жанама кернеу τ_z, τ_y – ішкі көлденең күштің қарқындығын немесе қарастырылған қиманың берілген нүктесінің аудан бірлігіне келтірілген көлденең күш : τ_z = dQ_z / dA, τ_y = dQ_y / dA

Жалпы алғанда, берілген нүктедегі кернеу элементар қиманың жазықтығына кез-келген α бұрышымен түсуі мүмкін.

Әлбетте, тік және жанама кернеулердің шамалары : σ =psin α, τ=pcos α

Демек толық кернеудің шамасы : p= √ σ²+ τ²

2. Сұрақ

Арқалықты жүйелер. Жүктемелердің түрлері. Машиналармен конструкцияларда өте жиі арқалық деп аталатын (немесе арқалықты жүйелер) созылған пішінді денелер кездеседі. Арқалық деп қандай да бір құрылымның түзу білік түрінде екі (немесе одан да көп) нүктесінде тірегі бар конструкциялық тетігін айтамыз.Алдыңғы тақырыптан белгілідей, жазық күштер жүйесінің тепе-теңдік шарты үш теңдеумен өрнектеледі.Олардың көмегімен жүктелген денені қарастыра отырып, денеге түсірілген қандай да бір күштердің шамасы бойынша байланыс реакцияларын, дара жағдайда тірек реакцияларын анықтауға болады. Осы ескпті шешудің жалпы аналитикалық әдісінің түйіні мынада : берілген дене тепе теңдікте болғандықтан,байланыс реакцияларын бірге есептегенде денеге әсер ететін күштердің барлығы тепе теңдік шартын орындауы қажет. Осы тұрғызылған тепе теңдік шарттарынан берілген күштермен қатар белгісіз рефкциялар енетін теңдеулер аламыз.Алынған теңдеулер жүйесін шеше отырып,белгізіс күштерді анықтаймыз.

Әрбір жазық күштер жүйесі үшін белгілі анықталған,сәйкес тепе теңдік теңдеулер саны болады.Мұнан,белгісіз күштер саны тұрғызылған тепе теңдік теңдеулердің санына тең болуы қжет. Егер белгісіз күштер саны теңдеулердің санынан аспаса,огда теңдеулерді шешуге болады. Мұндай есептерді статикалық анықталған деп атайды,ал егер белгісіз күштер саны теңдеулердің санынан асып түссе,есеп статикалық анықталмаған болады.Есепті статиканың әдістерімен шешуге болмайды.Статикалық анықталмаған есептерді,тек дененің серпімді қасиеттерін ескере отырып шешуге болдады,ал ол жағдай теориялық механикада қарастырылмайды.

Жүктеме түсу жағдайына байланысты екі түрге бөлінеді: қадалған және таралған күштер. Осыған дейін біз тек қадалған күштерді қарастырдық,яғни күшті бір нүктеге жинақталған деп. Шын жағдайда күшті бір нүктеге түсіру мүмкін емес,тек кейбір жағдайларда осылай сұлбалау орынды да.Мысалы арқалыққа түсірілгенбір цилиндрлік дене немесе арқалыққа сүйенген екі қабырғалық панель. Тірек реакцияларын анықтағанда арқалықты қадалған F₁және F₂ күштермен жүктелген деп қарастыруға болады.

Көптеген жағдайда қарастырылап отырған денеге тұтас жүктеменің түсірілуін ескермеуге болмайды. Тұтас жүктемеге судың плотинаға қысымы,тасымалдаушының лентасына құмның түсіретін қысымы мысал бола алады жіне т.б.

Таралған күштердің ішінен тек бір қалыпты таралған күштерді қарастырамыз. Мұндай жүктемелер шартты түрде тік төртбұрыш түрінде кескінделеді. Оның ішіне жүктеменің қандай бағытта әсер ететінін көрсететін параллель жебелер түсіріледі.Бірқалыпты таралған жүктеме екі параметрмен беріледі: қарқынымен q, яғни ұзындық бірлігіне (м) келетін күш бірлігімен(Н немесе кН) және ұзындықпен l. Статиканың есептерінде,абсолют қатты арқалыққа түсірілген бірқалыпты таралған күшті оған тең әсерлі Q қадалған күшпен алмастыруға болады.бұл күш таралған күш әсер ететін ұзындықтың ортасына түсіріліп, q қарқындығымен бағыттас болады. Оның шамасы жүктеме әсер ететін l ұзындықпен q қарқындықтың көбейтіндісіне тең.

Сонымен қатар арқалыққа кейбір жағдайда қос күш әсер етеді. Мұндай жағдайда қос күштің арқалыққа әсері, бізге белгілідей, оның моментімен М=Fa өлшенеді және шартты түрде доғалы жебемен кескінделеді.

15- билет

1-сұрақ

Құрылым элементтерінің созылу мен сығылуға қарсыласу сенімділігін , беріктігін қамтамасыз ететін өлшем келесі беріктік шарты деп аталатын шарттың орындалуы болып табылады

Ϭmax= Nmax/A≤ Ϭadt

Ϭmax –қауіпті қиманың қандайда бір нүктесіндегі шынайы ең үлкен кернеу

Созылған немесе сығылған стерженнің деформациялану шамасын сипаттау үшін абсалют ұзарудың стерженнің алғашқы ұзындығына ,ал абсалют қысқарудың стерженнің алғашқы еніне қатынастары ,яғни

ε=Δl/l

ε’=Δb/b

ε – бойлық Салыстырмалы деформация.

ε’ - ендік Салыстырмалы деформация.

Δl-абсалют ұзару

Δb- абсалют қысқару

2-сұрақ

Күштің денеге айналдырушы әсері Күш моменті деп аталады, . Күштің нүктеге қатысты моменті деп , плюс не минус таңбамен алынған күш модулі мен осы нүктеден әсер сызығына дейін түсірілген перпендикулярдың ұзындығына көбейтінісін айтады . Күштің өске қатысты моменті Күштің өске перпендикуляр жазықтықтағы проекциясының , өс пен жазықтықтың қиылысу нүктесіне қатысты моментінің алгебралық шамасына тең

16 - билет

1. сұрақ

Жинақталатын күштер жүйесінің тепе-теңдік шарты.

Әсер сызықтары бір нүктеде қиылысатын күштер жүйесі жинақталатын күштер жүйесі деп аталады . Кейде күштер көп бұрыш тұрғызғанда соңғы қосылатын күштің ұшы алғашқы күштің бас нүктесіне сәйкес келуі мүмкін , яғни жинақталатын күштер жүйесінің тең әсерлі күші нолге тең . Бұл жағдайда жинақталатын күштер жүйесі тепе-теңдікте деп аталады. Сонымен жинақталатын күштер жүйесі тепе-теңдікте болуы үшін күштер көпбұрышының тұйықталған болуы қажет және жеткілікті . Бұл тұжырым жинақталатын күштер жүйесі тепе-теңдікте болуының геометриялық шарты деп аталады.

Ȓ=F1+F2+….+Fn = ∑Fi =0

2. сұрақ

Иілу кезіндегі орын ауыстыру. Арқалықтың иілу өсінің универсал теңдеуі.

2 шамамен анықталады

У иілу шамасымен – деформацияланбаған арқалықтың бойлық өсіне перпендикуляр бағытта қиманың ауылық центрінің орын ауыстсруы

Ѳ бұрылу бұрышымен - қиманың алғашқы күйіне қатысты бұрылуы немесе оған тең серпімді сызыққа жүргізілген жанама сызығының деформацияланбаған арқалық өсімен құратын бұрышы

17- билет

1. Сұрақ

Жазық жинақталатын күштер жүйесінің тең әсерлі күшін анықтаудың аналитикалық әдісі. Бір нүктеге түсірілген екі күштің тең әсерлі күшінің модульі мен бағытын аналитикалық тәсілмен де анықтауға болады, ол үшін АВС үшбұрышын қарастырайық. Бұрыш BAD=φ, Бұрыш ABC =π-φ.

Косинустар теоремасы бойынша R²=F₁²+F₂² – 2F₁F₂cos(π-φ) =F₁²+F₂²+2F₁F₂cos φ,

Бұдан тең әсерлі күші модульі, R= √F₁²+F₂²+2F₁F₂cos φ

Синустар теоремасы бойынша, F₁ / sinα = R / sin (π-φ) = R /sin φ

Осы тепе теңдіктен тең әсерлі күштің әсер ету бағытын анықтаймыз sinα = F₁ sin φ / R.

Екі күшті қосудың дербес жағдайларын қарастырайық:

1. Егер φ =0 болса, онда ( R= F₁+F₂)

Қатты дененің бір нүктесіне бір түзудің бойымен бір бағытта түсірілген екі күштің тең әсерлі күшінің шамасы күштер шамаларының қосындысына тең және сол түзудің бойында күштер бағытымен бағытталады.

2. Егер φ =180 болса, онда (R=F₁ – F₂)

Қатты дененің бір нүктесіне бір түзудің бойымен қарама қарсы бағытта түсірілген екі күштің тең әсерлі күшінің шамасы күштер шамаларының айырылымына тең және сол түзудің бойында үлкен күш бағытымен бағыттас болады

3. Егер φ =90 болса, онда R = √ F₁²+F₂²

Қатты дененің бір нүктесіне өзара перпендикуляр түсірілген екі күштің тең әсерлі күшінің шамасы мен бағыты осы күштерден тұрғызылған тіктөртбұрыштың диоганаліна тең.

2. Сұрақ

18-билет

1. Сұрақ

Материалдар кедергісінде беріктік, қатаңдық және орнықтылық мәселелерін

қарастырғанда бізге білік қималарының ауданынан басқа да сипаттамалары қажет болады. Олар қиманың күрделі геометриялық сипаттамалары деп аталады.

Статикалық моменттері. Ауырлық ортасының координаталары.

Фигураның ауданының осьтерге қатысты статикалық моменттері:

Sx = ∫ y dA, Sу = ∫ х dA

мұндағы х, у - dA- элементар ауданының Х,У осіне дейін арақашықтығы,

интеграл аудан А бойынша алынады (1-сурет). Бұл шаманың өлшем бірлігі,

көбінесе см³. Бұл шама оң, теріс таңбалы және нөлге тең болуы мүмкін.

Бұл шамаға мынандай теңдеу жазуға болады:

Sx = ∫ ydA = А∙yc, Sу = ∫ хdA = А∙хc

мұндағы А - фигураның толық ауданы, хc, yc - фигураның ауырлық ортасының

Х,У осіндегі координаталары.

Осы формуладан ауырлық ортасының координаталары анықталады:

Sz = yc*A, Szy= zc*A

Осы формулалардан мынандай ереже алынады:

Егер Z және У осьтері фигураның ауырлық орталықтарынан өтсе, онда ол осы осьтерге қатысты статикалық моменттер нөлге тең. Бұл осьтерді орталық осьтер деп атайды.

Қиманың белгілі бір оське қарағандағы статикалық моменттері сол

фигураны құрайтын қарапайым фигуралардың статикалық моменттерінің

қосындысына тең (егер фигура бөліктерге жіктелсе).

Қиманың остік, полярлық және ортадан тепкіш екпін моменттері.

Берілген қиманың кез келген Z, У осьтеріне қатысты осьтік екпін моменттері деп төмендегі интегралдармен анықталатын геометриялық сипаттамаларын айтады

Jz = ∫y²dA, Jy = ∫x²dA

Мұндағы z, у- dA- элементар аудан мен Z,У остерінен арақашықтықтары.

Берілген қиманың полюс деп аталатын кез келген нүктеге қатысты өрістік екпін моменті деп төмендегі интегралмен анықталатын геометриялық сипаттаманы айтады:

Jρ = ∫ρ²dA

мұндағы ρ – полюстен шексіз кіші ауданға дейінгі ара қашықтығы.

Берілген қиманың кез келген өзара перпендикуляр Z,У осьтерге қатысты

центрден тепкіш екпін моменті:

Jzу = ∫zуdA

Центрден тепкіш инерция моментінің таңбасы оң, теріс, кей жағдайларда

нөлге тең болуы мүмкін. Инерция моменттерінің өлшем бірлігі –см³

2. Сұрақ

Денелердің өлшемдері мен пішіндерінің өзгеруін деформация деп атайды. Брустың В бөлігінен А қимасы арқылы С бөлігіне ішкі күштер үздіксіз жайылып таралып беріледі (І. 6, б - сурет). Жалпы жағдайда, бұл ішкі күштер қиманың ауырлық центрі арқылы өтетін, басты вектор деп аталатын R күшіне және басты момент деп аталатын М моментіне келтіріледі (І. 6, в - сурет). Басты векторды OX, OY, OZ осьтерінің бойында жатқан құраушы күштеріне, ал бас моментті құраушы моменттеріне жіктейік. Бұл құраушы күштер мен моменттер ішкі күш компоненттері немесе факторлары деп аталады. - көлденең қимаға перпендикуляр бойлық ось бойымен әсер етеді, сондықтан оны бойлық күш деп, ал OX, OY осьтеріне параллель әсер ететін ішкі күштерін көлденең немесе жанама күштер деп атайды. моменттерін ию, ал моментін бұрау моменттері деп ажыратады.

Сыртқы күштердің әсерінен пайда болған денедегі серпімді деформация дененің өлшемдеріне қарағанда шексіз кіші, сондықтан, дененің бөліктері үшін теориялық механиканың келесі тепе – теңдік теңдеулерін қолдануға болады

1) 2) 3)

4) 5) 6) І.03

Бірінші үш теңдеуден ішкі күштері, ал соңғы үшеуінен ішкі моменттері анықталады. Бұл мысалда брусқа әсер ететін сыртқы күштер бір жазықтықта жатпайды деп жалпы жағдайды қарастырдық. Енді іс жүзінде жиі кездесетін қарапайым жағдайларды атап өтейік.

Егер дененің кез келген көлденең қимасында тек қана пайда болса, деформация бұралу деп аталады.

19- билет

1. Сұрақ

Материалдардың механикалық қасиеттерін тәжірибелік зерттеу. Материалдардың сыртқы күш әсеріне қарсыласу қабілеті мен деформациялануы немесе қирауы олардың механикалық қасиеттеріне тікелей байланысты. Материалдардың механикалық қасиеттері тәжірибе жүзінде арнайы үлгілерді сынау арқылы анықталады. Үлгіні жүктеудің түрлеріне, байланысты сынау статикалық, динамикалық, циклды сынау деп, ал үлгінің деформациялану ерекшеліктеріне байланысты созуға, сығуға, июге, бұрауға сынау деп т.б. кӛптеген түрлерге бӛлінеді. Жеке жағдайларда үлгілер бұралып иілу, бұралып сығу сияқты күрделі деформацияларға сыналады. Сынау нәтижесінде алынатын механикалық сипаттамалар материалдардың жұмыс істеу шарттарына, температураға, қоршаған ортаға, күш әсерінің ӛзгеруі жылдамдығына т. б. факторларға байланысты ӛзгеріп тұрады. Сондықтан материалдардың механикалық қасиеттерін ӛзара салыстыру үшін оларды қатаң түрде бірдей жағдайларда сынайды.

Сынама үлгілердің формалары мен ӛлшемдері, оларды сынау шарттары мемлекеттік стандартта қарастырылып бекітілген.

Созу диаграммалары. Сан алуан сынау тәсілдерінің ішінде кең тарағаны – материал үлгілерін созуға сынау. Ӛйткені, созуға сынау нәтижесінде алынатын механикалык шамалар, материалдардың сыртқы күшке қарсыласу қабілетін, деформациялануын немесе қирау ерекшеліктерін айтарлықтай толық сипаттайды.

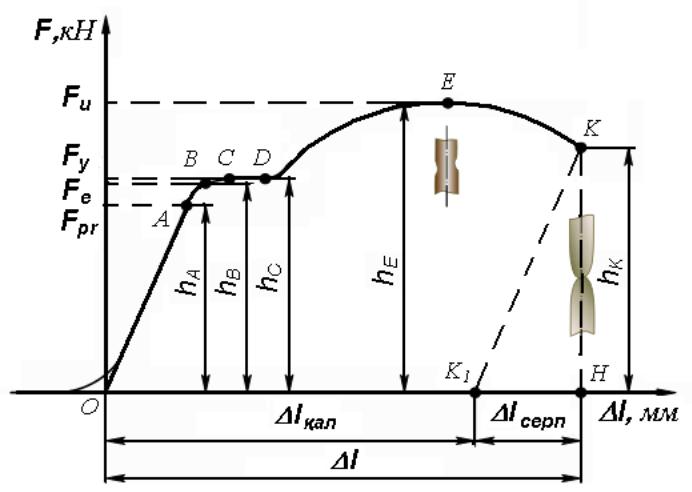
2. Сұрақ

Ауырлық центрі.

Ауырлық центрі  немесе Масса центрі - жүйені қозғалтқан кезде жүйенің барлық массасы жинақталған материалдық нүкте сияқты қозғалатын механикалық жүйедегі массаның таралуын сипаттайтын нүкте, қатты дененің кеңістіктегі кез келген қалпында оның бөлшектеріне тең әсерлі күшпен түсетін ауырлық күшінің геометриялық нүктесі; бұл нүкте кей жағдайда осы дененің ешбір нүктесімен сәйкес келмеуі мүмкін (мысалы, сақинада). Біртекті ауырлық өрісіндегі қатты дененің ауырлық центрі оның массалар центріне сәйкес келеді.

20- билет

1. Сұрақ

ИНЕРЦИЯНЫҢ БАС ӨCTEPI, БАС MOMEHTTEPI

Алдыңғы параграфта алынған 5.08, 5.09, 5.10 формулаларына қарап инерция моменттерінің тек бұрышына (5.5-сурет) тәуелді екенін байқауға болады. Олай болса, өстің инерция моменттерінің экстремальді, мәндеріне сәйкес бұрышының мәнін анықтауға болады. Ол үшін 5.08 немесе 5.09 өрнегінен біp рет туынды алып, оны нөлге теңестірсек болғаны.

осыдан

(5.11)

Алынған формула бойынша бұрышының екі мәні бар: біpі ao екіншісі 90°; демек инерция моменттерінің мәні экстремальды өзара перпендикуляр екі-ақ өс бар. Бұл өстер бас өстер деп аталады, оларға қарағандағы өстік инерция моменттері бас инерция моменттері деп аталады. Бас өстерге

қарағандағы центрден тепкіш инерция моменті нөлге тең.

Енді 5.08 және 5.09 өрнектеріндегі -нің орнына қойып, бас инерция моменттерің анықтаймыз (5.5-сурет).

Өрнектерді тригонометриялық функциялардан босатып басты инерция моментерінің формулаларын келесі түрге келтіруге болады

. (5.12)

Өстік инерция моменті мен қима ауданының арасындағы байланыс арқылы табылатын шаманы

,

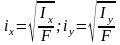қиманың инерция радиусы деп атайды.

Жарты өстері бас инерция радиустеріне тең ( ), бас өстерге тұрғызылған эллипс – инерция эллипсі деп аталады, келесі теңдеумен өрнектеледі

Инерция эллипсінен кез келген центрлік өске карағандағы инерция моментін табуға болады. Мысалы, X_i өсіне қарағандағы инерция моментін табу үшін, осы өске параллель эллипске жанама жүргізіледі. Эллипс центрінен жанамаға түсірілген перпендикулярдың (СА) ұзындығы инерция радиусының (i_x) шамасына тең (5. 9-сурет). Инерция радиусы арқылы, инерция моментін келесі формуламен анықтауға болады

.

2. Сұрақ

Статиканың аксиомалары. Дененің тепе-тендікте болу шарттары өмірлік тәжірибеден негізделген және дәлелдеусіз қабылданатын бірнеше жағдайға негізделіп қорытылады.

Оларды статиканың аксиомалары деп ат.

Статиканың нег аксиомаларын Ньютон тұжырымдаған.