1-билет

Жазық қималардың екпін инерция моменті

Интегралдармен анықталатын геометриялық сипаттамаларды қиманың статикалық моменттері дейміз.

Берілген қиманың кез келген өзара перпендикуляр өстеріне қарағандағы центрден тепкіш екпін моменті деп, төмендегі интегралмен анықталатын геометриялық сипаттаманы айтамыз:

Параллель осьтерге қатысты екпін моменттерінің байланысы (өзгеруі).

Бұл тәуелділікті анықтау үшін, ауданы қиманы (I.2.25 - сурет) қарастырайық. Қиманың ауырлық центрінен өзара перпендикуляр өстері жүргізілген. Ауырлық центрден өтетін өстерді центрлік өстер деп, ал центрлік өстерге қарағандағы екпін моменттерін центрлік екпін моменттерідеп атаймыз.

Қиманың центрлік екпін моменттері берілген деп қарастырып, центрлік өстерге параллель өстеріне қарағандағы екпін моменттерінің шамаларын анықтайық.

Бөлініп алынған шексіз кіші ауданының жүйесіндегі координаттары , ал жүйесіндегі координаттары болсын. Онда, анықтама бойынша, қиманың өсіне қарағандағы екпін моменті

Анықтама бойынша, мұндағы

; ;

және центрлік өске қарағандағы қиманың статикалық моменті нөлге тең, олай болса

Дәл осылай және анықталады, сонымен

;

; (I.2.54)

,

яғни, қиманың кез келген центрлік өсіне параллель өске қарағандағы өстік екпін моменті, центрлік екпін моментіне қиманың ауданын осы өстердің ара қашықтығының квадратына көбейтіп қосқанға тең, ал центрден тепкіш екпін моменті, центрлік өстерге қарағандағы центрден тепкіш екпін моментіне қиманың ауданын осы өстердің ара қашықтықтарына көбейтіп қосқанға тең.

Бұралған осьтерге қатысты екпін моменттерінің байланысы (бұралуы).

Суретте көрсетілген (I.2.26 - сурет) қиманың және өстеріне қарағандағы және екпін моменттері берілген болсын делік. Енді өс жүйесін қандай да бір бұрышына бұрайық және, әмендегідей, сағат тіліне қарсы бұрылған бұрышты оң таңбалы деп ұйғарамыз. деп қабылдайық. Жаңа және өстеріне қарағандағы екпін моменттерін анықтайық.

Ол үшін, шексіз кіші ауданының пен жүйелеріндегі координаттарының арасындағы өзара байланысын анықтайық ( )

Олай болса,

жалпы (I.2.35) заңдылыққа байланысты

.

Центрден тепкіш екпін моментін (1.38) өрнегінен табамыз

Сонымен,

(I.2.55)

(I.2.56)

(I.2.57)

Алынған (I.2.55) және (I.2.56) өрнектерін қоссақ

екенін көреміз, яғни өзара перпендикуляр өстерге қарағандағы екпін моменттерінің қосындысы осы өстерді кез келген бұрышқа бұрғаннан өзгермейді.

2. сұрақ

Статиканың аксиомалары. Дененің тепе-теңдікте болу шарттары өмірлік тәжірибеден негізделген және дәлелдеусіз қабылданатын бірнеше жағдайға негізделіп қорытылады.

Оларды статиканың аксиомалары деп атайды.

Статиканың негізгі аксиомалары ағылшын ғалымы Ньютон (1642-1727) тұжырымдаған, сондықтан да олар ғалымның атымен аталады.

1 - аксиома(екпін аксиомасы немесе Ньютонның бірінші заңы).Қандай да болмасын күштер мәжбүр етпесе, дене тыныштықтағы немесе бірқалыпты түзу сызықты қозғалыстағы күйін сақтай алады.

Екпін немесе екпіндік деп, қозғалыстағы заттық дененің күш әсері болмаса да қозғалысын сақтайтын немесе күш әсерінен қозғалысын біртіндеп өзгертетін мүмкіндігін атайды.

2 - аксиома(екі күштің тепе-теңдік шарты).Екі күш түскен еркін қатты дене тепе-теңдігі үшін, күштердің шамалары (модульдері) тең және әсер сызықтары бір болып қарама-қарсы бағытталуы қажет және жеткілікті, яғни , егер және (I.1.9 - сурет).

Басқаша айтқанда, екі күш тепе-теңдікте болу үшін, олардың модульдері тең болуы және бір түзу бойымен қарама–қарсы бағытталуы қажет және жеткілікті.

3 - аксиома(теңестірілген күштерді қосу не алып тастау, шығару принципі).Кез келген күштер жүйесіне нөлге эквивалент күштер жүйесіне қосқаннан немесе алып тастағаннан (шығарғаннан) берілген жүйенің қатты денеге жасайтын әсері өзгермейді.

Егер және екі күштер жүйесі болса, онда бұл аксиома былай жазылады

4 - аксиома(параллелограмм ережесі). Қатты дененің бір нүктесіне түсірілген екі күштің тең әсерлі күшін,ің шамасы мен бағыты берілген күштерден құрылған параллелограмм диагоналымен анықталады да, сол нүктеге түсіріледі.

Қабырғалары берілген векторлар болатын параллелограмм диагоналын тұрғызуды (I.1.10, а - сурет) векторлық немесе геометриялық қосу деп атайды. Демек, бір нүктеге түсірілген екі күштің тең әсерлі күші осы күштердің векторлық қосындысына тең

және сол нүктеге түсіріледі.

Күш параллелограммен қатар екі жүйенің тең әсерлі күшін, күш үшбұрышымен де анықтауға болады. (I.1.10, b - сурет). Тең әсерлі күштің шамасы I.1.10, b, c - суреттерінен көрінетіндей векторлардың қосылу тәртібіне байланысты емес, яғни

5 – аксиома (әсер және қарсы әсер заңы).Екі дене бір–біріне әрқашан модульдері тең, бір түзу бойымен қарама-қарсы бағытталған күштермен әсер етеді.

Бұл аксиома физикада Ньютонның үшін,ші заңы деп аталады. Бесінші аксиома механикада өте маңызды орын алады. Егер денесі денесіне күшімен әсер етсе, денесі денесіне дәл осы сияқты модульді күшімен қарама-қарсы бағытта әсер етеді (I.1.11 - сурет). және күштерінің модульдері тең, ал бағыттары бір түзу бойымен қарама-қарсы бағытталса да, олар әр денеге түсірілгендіктен тепе-теңдіктегі күштер жүйесін құра алмайды. Бұл күштердің бірін тура әсер етуші күш деп қараса, екіншісі қарсы әсер күш болып табылады. Сонымен аксиома бойынша әрбір әсерге оған тең және қарама-қарсы бағытталған қарсы әсер болады. Осыдан барып табиғатта сыңар күш болмайтыны, әрбір күшке үнемі онымен бірге екінші бір қарама-қарсы күш сәйкес келіп отыратыны байқалады.

6 – аксиома (қатаю ережесі).Деформацияланатын дене абсолют қатты денеге айналса да механикалық күйі өзгермейді.

Басқаша айтқанда, берілген күштер жүйесі әсерінде тұрған деформацияланатын дене тепе-теңдігі, егер дене мезетте қатайса да, яғни абсолют қатты денеге айналса да өзгермейді.

Бұл ережеден абсолют қатты дененің тепе-теңдігінің қажет және жеткілікті болатын шарттарының деформацияланатын дене тепе-теңдігі үшін тек қажетті ғана болып, жеткілікті болмайтындығы көрінеді. Мысалы, егер күштер әсеріндегі резенкеден жасалған дене оның тепе-теңдігі дене абсолют қатты денеге айналса да сақталады. Ал бірақ та күштер тепе-теңдікте тұрған абсолют қатты дене бірден резенкеден жасаған денеге айналса, онда дене тепе-теңдік күйін сақтай алмауы мүмкін.

2- билет

1. Сұрақ

Күш. Табиғаттағы заттық денелер әрдайым өзара немесе қоршаған ортамен әсерде болады.

Күшдеп денелердің өзара механикалық әсерлерінің өлшемін атайды. Күнделікті тұрмыста, техника саласында күштің денеге әсері оның шамасы (модулі), бағыты және түсу нүктесі арқылы анықталатынын көреміз. Бұдан күшті векторлық шама деп қарастыруға болатындығы шығады.

Физикадан белгілідей күш шамасы динамометрдің жәрдемімен өлшенетін салмақ арқылы анықталады.

Механикада күштің өлшем бірлігі ретінде физикалық шамалардың өлшеу бірліктерінің халықаралық системасынада (СИ) 1 Ньютон алынады.

Ньютон деп массасы 1 кг денеге күш әсері бағытында 1м/с² үдеу беретін күш аталады. Ньютонның еселік бірліктері – килоньютон (1кН = 10³Н) және меганьютон (1МН = 10⁶Н).

Күшті кез келген вектор сияқты бағытталған кесіндімен бейнелеуге болады. Вектор - тың АВ кесінді ұзындығы (I.1.1- сурет) белгілі бір масштабта алынған сан мәнін (модулін) бейнелейді, ал оның бағыты күштің әсер ету бағытына дәл келеді. Ол вектордың бас нүктесі А күштің денеге әсер ететін нүктесіне сәйкес болады. Дененің күш әсер етіп тұрған А нүктесі күштің түсу нүктесі деп, ал бойымен күш векторы бағытталған сызығын күштің әсер ету сызығыдеп атайды.

Қандай да бір денеге бір мезгілде әсер ететін күштер жиынын күштер жүйесі деп атайды.

Күштер жүйесі дөңгелек жақшалар ішінде алынған күш векторларымен белгіленеді. Мысалы: - күштен тұратын күштер жүйесі.

Дененің механикалық күйін өзгертпей әсер етуші күштер жүйесін тепе–теңдіктегі күштер жүйесі деп немесе нөлге эквивалентті (пара-пар) күштер жүйесі деп атайды

Денеге бірдей механикалық әсер етуші әр түрлі күш жиындары бір-біріне эквивалент жүйелер деп аталады.

Эквивалент екі күштер жүйесінің қандай да болмасын бір денеге әсерлері бірдей болғандықтан, олардың біреуін екіншісімен алмастыруға болады.

Қатты денеге түсірілген күштер жүйесі бір күшке эквивалент болса, онда ол күшті берілген күштер жүйесінің тең әсерлі күшідеп атайды

Берілген күштер жүйесінің теңестіруші күші осы жүйенің теңгеруші күші деп аталады.

2. Сұрақ

3- билет

1. Сұрақ

Аз көміртекті болаттың созылу диаграммасы және оның механикалық сипаттамалары.Аз көміртекті болатты созып сынаған кезде алынатын созу диаграммасы суретте корсетілген. Диаграмманың абсцисса осінде үлгінің деформациясы абсолют шамасы, ал ордината осінде деформация тудыратын күш өрнектелген бұл диаграммадан төмендегідей негізгі механикалық сипаттамалар анықталады:

• Гук заңына бағынышты аралықтағы (диаграммада ОА – аралығы) ең үлкен кернеу δ_pr. Бұл кернеу δ_pr – пропорционалдық шек деп аталады да келесі өрнекпен анықталады δ_pr=F_pr/A₀ мұндағы F_pr – пропорционалдық шекке сәйкес күштің шамасы, A_{0 –} үлгінің жүктемеге дейінгі көлденең қимасының ауданы.

• Қалдық немесе пластикалық деформация тудырмайтын кернеудің ең үлкен шамасын (диаграмма В нүктесінде) серпімділік шегі деп атап, келесі өрнекпен анықталады δ_е=F_е/A₀ мұндағы F_е – серпімділік күшке сәйкес күштің массасы. Материалдардың серпімділік шегінің шын мәнін анықтау өте қиын, көп уақытты және дәл өлшегіш құралдарды пайдалануды қажет етеді. Сондықтан да көп жағдайларда δ_pr мен δ_е бір біріне тең деп алынады.

• Деформацияның өсуі күштің тұрақты мәнінде өтетін кернеуді ең аз шамасын (диаграммада СД аралығы) аққыштық шегі деп атап, келесі өрнекпен есептейді δ_у=F_у/A₀ мұндағы F_у – аққыштық күшке сәйкес күштің массасы.

• Диаграмманың ең эоғарғы нүттесіне сәйкес келетін (диаграммада Е нүтесі) кернеу беріктік шегі деп аталады, δ_u=F_u/A₀ формуласымен анықталады. F_u - беріктік шекке сәйкес күштің шамасы. Материалдың беріктік шегін уақытша қарсыласу шегі деп те атайды.

• Үзіле кезіне сәйкес келетін кернеу шамасы қирау шегі деп аталып, δ_r=F_r/A₀ формуласымен анықталады. F_r - қирау шекке сәйкес күштің шамасы.

Диаграмманың осы аталған кемшіліктерін болдырмау үшін ордината осін δ=F/A₀ арқылы, ал абсцисса осін ε=∆l/l₀ арқылы өрнектейтін диаграмма тұрғызылады. Бұл диаграмма шарты кернеу диаграммасы деп аталады. Өйткені бұл диаграммадағы механикалық сипаттамалар – δ_pr, δ_e, δ_y, δ_u, δ_r – үлгінің сынауға дейінгі бастапқы қима ауданы арқылы анықталған.

2. Сұрақ

Қос күш және оның денеге әсері. Қос күштің негізгі қасиеттері.

Модульдері тең және қарама қарсы баытталған екі параллель күш жүйесін қос күш деп атайды. XIX ғасыр басында француз ғалымы Пуансо (1777-1859) механикаға қос күш ұғымын енгізіп, қос күштер теориясын тұрғызады.

Қос күшті құрайтын күштер орналасқан жазықтық қос күш әсерінің жазықтығы, ал күштерлің ең жақын ара қашықтығы d қос күшінің иіні деп аталады. Қос күштің денеге әсері денені айналмалы қозғалысқа келтіруге тырысатынымен спатталады. Қос күш моменті деп + не – таңбамен алынған қос күшті құраушы күштердің бірінің модулі мен оның иінінің көбейтіндісін айтады M(F₁,F₂)=F*d. Егер қос күш денеі сағат тілі жүрісімен бағыттас айналдыруға тырысса, онда кос күш моменті теріс таңбалы, ал егер сағат тілі жүрісіне кері бағытта айналдырса қос күш моменті оң таңбалы деп алу ұйғарылған.

Қос күштің 3 қасиеті бар:

1. Қос күштің тең әсерлі күші болмайды.

2. Қос күштің құраушы күштерінің әсер жазықтығындағы кез келген нүктеге қатысты алынған моменттерінің алгебралық қосындысы қос күш моментіне тең. Қос күштің бұл қасиетін былай тұжырымдауға болады: кез келген момент центрлеріне қатысты құрылған момент теңдеулеріне қос күш бірдей таңбамен және бірдей шамамен кіреді, яғни қос күш моментінің таңбасы мен шамасы момент центрінің орнына туелсіз.

3. Қос күштің құраушы күштерінің кез келген осьтегі проекцияларының алгербралық қосындысы әрқашан нөлге тең.

4- билет

1. Сұрақ

Параллель өстерге қарағанда инерция моментерінің арасындағы тәуелділік

Қиманың өзара перпендикуляр X, У центрлік өстеріне қарағандағы

4 .4-сурет

инерция моменттері белгілі дейік. Енді осы өстерге параллель жаңа өстеріне қарағандағы инерция моменттерінің шамаларын анықтайық (5.4-сурет). Бөлініп алынған тің ХОУ жүйесіндегі координаттары х, у, ал жүйесіндегі координаттары = x+a, 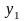=y+b болсын.

Фигураның және өстеріне қарағандағы инерция моменттері төмендегі интегралдар мен анықталады

Бұл өрнектердегі интегралдары, центрлік Х, У

өстеріне қарағандағы статикалық моменттер болғандықтан нөлге тең, олай болса:

. (5.06)

Сонымен, фигураның кез келген центрлік өсіне параллель өске қарағандағы өстік инерция моменті, центрлік өстік инерция моментіне, фигураның ауданын осы өстердің ара қашықтығының квадратына көбейтіп қосқанға тең. Центрлік өске қарағандағы өстік инерция моменті, осы өске параллель, кез келген өске қарағандағы өстік инерция моменттерінен кіші.

Фигураның өзара перпендикуляр центрлік өстеріне параллель өстерге қарағандағы центрден тепкіш инерция моменті, фигура ауданының осы өстердің ара қашықтықтарына көбейтіп қосқанға тең (5.4-сурет).

Жалпы жағдайда, күрделі фигуралардың инерция моменттері келесі формулалармен анықталады

(5.07)

2. Сұрақ

Статиканың қарапайым теоремалары. Күшті әсер сызығы бойымен көшіру теоремасы.Кез келген күшті, әсер ететін дененің механикалық күйін өзгертпей-ақ өзінің әсер сызығы бойымен басқа нүктеге көшіруге болады.

күші қатты дененің нүктесіне түсірілген, осы күшті әсер сызығы бойындағы қандай да бір нүктесіне көшіру қажет делік (I.1.12, а - сурет). күшін,ің әсер сызығы бойымен нүктесіне өзара тең, қарама-қарсы бағытталған және күштерін түсірейік (I.1.12, b - сурет). Бұл күштердің шамасы берілген күшінің шамасына тең болсын және

_{сондықтан да} нүктесіндегі екі күш нөлге эквивалент болатын жиын құрайды, онда

Үшінші аксиома бойынша

Соңғы үш күштен тұратын жүйеде және күштері екінші аксиома бойынша

Олай болса, үш күштен тұратын жүйеден оларды алып тастауға болады.

Бұл дегеніміз нүктесіне түсірілген күшін, әсер сызығы бойынша нүктесіне көшірілгенмен пара-пар (I.1.12, с - сурет). Теорема дәлелденді.

Сонымен, денеге әсер ететін күшін, өзінің әсер ету сызығының бойымен кез келген нүктеге көшіруге болады.

Әсер сызығы бойынша көшіруге болатын векторларды сырғыма векторлар деп атайды. Демек қатты денеге әсер етуші күштер де сырғыма векторлар болып табылады.

Үш күш туралы теорема.Егер бір-біріне параллель емес, бір жазықтықта жататын үш күш тепе-теңдіктегі күштер жиынын құрайтын болса, онда күштердің әсер сызықтары бір нүктеде қиылысады.

Қатты дененің нүктелерінде бір жазықтықта жатқан, өзара параллель емес күштері берілсін делік (I.1.13 - сурет) және күштерінің әсер сызықтары бір нүктеде қиылысатын болсын. және күштерін әсер сызықтары бойымен нүктесіне көшіріп, параллелограмм ережесі бойынша осы күштердің тең әсерлі күшін, анықтайық

Олай болса,

_{Теорема шарты бойынша}

Сондықтан,

Екінші аксиомаға сәйкес, екі күштің тепе-теңдікте болуы үшін олар бір түзудің бойымен қарама-қарсы бағытталулары қажет. Олай болса үшінші күштің де әсер сызығы нүктесінен өтуге тиісті. Сонымен теорема дәлелденді.

5- билет

1. Сұрақ

Қос күштердің эквиваленттілігі .

Еркін қатты дененің механикалық күйін өзгертпей бір қос күшті екінші бір қос күшпен алмастыруға мүмкн болса, онда бұл қос күштер пара-пар немесе эквивалентті деп аталады.

1-теорема. Қос күштің денеге әсері, оны әсер ету жазықтығында басқа орынға ауыстырғаннан өзгермейді.

Иіні АВ=l (F₁,F₁ˈ) қос күші беріліп, қос күштер иіні A₁B₁=l болатын кездейсоқ алынған орынға ауыстыру қажет болсын делік.

A мен В және А₁ мен В₁ нүктелерінен, сәйкесінше АВ және А₁В₁ кесінділеріне перпендикуляр, параллель түзулер жүргізейік. Екі параллель түзудің екінші параллель түзумен қиылысады және қиылысында СDEK ромб пайда болады (өйткені берілгені бойынша AB=A₁B₁=l, ал параеллелограмның бір төбесінен түсірілген биіктіктер тең болса, онда ол ромб). F­₁ күшін әсер ету сызығының бойымен А нүктесінен С нүктесіне, ал F₁ˈ күшін В нүктесінен Е нүктесіне түсірейік. СА₁ түзуінің бойымен С нүктесіне, модульдері F₁ ­–ге тең теңестірілген F₂ және F₃ күштер жүйесін түсірейік; DB₁ түзінің бойымен Е нүктесіне де модульдері F₁ˈ -ке тең, теңестірілген F₃ˈ және F₂ˈ күштер жүйесін түсірейік, сонымен F­­­_1­­­ =F₂=F₃= F­­­_1­­­ˈ=F₂ˈ=F₃ˈ.

C нүктесіне түсірілген F­­­_1­­­ және F₃ күштерінің тең әсерлі R_c күшін және Е нүктесіне түсірілген F­­­_1­­­ˈжәне F₃ˈ күштерінің тең әсерлі R_E күшін анықтайық. R_c және R_E күштері бірін-бірі теңестіретінін аңғару қиын емес, өйткені олардың шамалары өзара тең және олар CDEK ромбасының диагональінің бойымен қарама-қарсы бағытта әсер етеді. Сонымен F­­­_1­­­, F₃, F­­_1­­­ˈ және F₃ˈкүштері теңестірілген күштер жүйесін құрайды, яғни { F­­­_1­­­,F₃, F­­­_1­­­ˈ,F₃ˈ}~0. Олай болса оларды қарастырмай-ақ қоюға болады, сонда қарастырылған күштер жүйесінен тек екі күш қалады, С нүктесіндегі F₂ күші мен Е нүктесіндегі F₂ˈ күші. Бұл күштерді әсер сызықтарының бойымен жылжыта отырып, сәйкесінше А₁ және В₁ нүктелеріне түсірсек, онда иіні АВ болатын (F₁, F₁ˈ) қос күштеріне пара-пар келетін иіні А₁ В₁-ге тең (F₂,F₂ˈ) қос күшін аламыз, өйткені F₁, F₁ˈ, F₂ және F₂ˈ күштерінің модульдері және АВ мен А₁ В₁ иіндері тең. Сонымен, берілген қос күшті басқа орынға ауыстырдық. Бұл теореманың дәлелденгендігін көрсетеді.

2-теорема. Моменттері өзара тең бір жазықтықтағы екі қос күштің денеге әсерлері бірдей болады.

Иіні АВ=l₁ (F₁, F_1­ˈ) қос күші берілсін делік. Онда, қос моменті М₁=F₁l₁ болады.

Қос күшке АВ иіні бойымен әсер ететін теңестірілген F пен Fˈ күштерін біріктірейік және F₁ мен F, сонымен қатар F₁ˈ пен Fˈ күштерін қос-қостап қосайық. Олардың тең әсерлі күштері F₂ мен F₂ˈ, иіні AC=l₂ тең жаңа қос күшті құрайды. Жоғарыда келтірілген түрлендірулер статиканың аксиомаларына негізделіп жүргізілді және дененің алғашқы күйін еш өзгертпейді, яғни (F₂,F₂ˈ) қос күші денеге (F₁, F₁ˈ) қос күшіндей әсер етеді. Енді қос күштердің моменттерінің теңдігін дәлелдеу керек:

(F₁, F₁ˈ) қос күшінің моменті М₁=F₁l_1,

(F₂, F₂ˈ) қос күшінің моменті М₂=F₂l_2.

Сызбадан l₂=l₁cosα , F₂=F₁/cosα екені көрінеді, олай болса, M₂=F₂l₂=(F₁/cosα)l₁cosα=F₁l₁, яғни М₂=M₁.

Теорема дәлелденді!!!!!!!!!!!!

2. Сұрақ

Дағдарыс күш. Эйлер формуласының қолдану шегі.

Бойлық июді туындататын ең кіші сыртқы сығу күшін дағдарыс күш деп атайды. Сығылған стерженьді орнықтылыққа есептеудің мәнісі мынада: оның бойлық F күштің қандай да бір мәнінде түзу сызықты орнықтылығын сақтауы мен қандай да бір орнықтылық қорының болуы.

Дағдарыс күшті анықтайтын формуланы ең алғаш 1774 жылы Л. Эйлер жариялаған. Дағдарыс күштің стержень ұштарының бекітілуіне тәуелді болғандықтан, біз дағдарыс күштің әр түрлі жағдайға сай мәнін анықтаймыз.

Бойлық өсі бойымен сығылған топсалы қос тіректі, ұзындығы l стерженьді қарастырайық. Егер сығушы күштің шамасы дағдарыс күшіне тең немесе онан асқан жағдайда стержент орнықтылығын жоғалтып, иіледі. Онда оның әрбір қимасындағы ию моменті

M= -F_cry.

Теріс таңба ию моментінің таңбалары туралы ереже бойынша алынған: иілген арқалықтың дөңес жағы төмен жатса, ию моменті оң, иілу мөлшері теріс таңбалы, ал дөңес жағы жоғары болса, ию моменті теріс, иілу мөлшері оң таңбалы.

Егер стерженнің серпімді сызығы синусоидалы кескіндейді деп қабылдасақ, онда стерженнің ортасына сәйкес келетін иілу мөлшерінің ең үлкен шамасын f деп отырып, серпімді сызықтың теңдеуін былайша жазуға болады

y=fsin(П/l)x,

олай болса,

M= -F_crfsin(П/l)x.

Серпімді сызықтың жалпы дифферинциалдық теңдеуіне назар аудрып, алынған моменттің мәнін қойсақ, онда серпімді сызықтығ дифференциалдық теңдеуі былай өрнектеледі

(EI)d²y/dx² = - F_crfsin(П/l)x.

Бойлық иілген стержень орнықтылығын үнемі ең кіші қатаңдық жазықтығында жоғалтады, олай болса, I стерженьнің көлденең қимасының центрлік өстік екпін моментінің ең кіші мәніне тең деп түсінген жөн, яғни I=I_min.

Алынған дифференциалдық теңдеуді бір рет интегралдайық

(EI_min)dy/dx=F_crf(l/П)cos(П/l)x+C_1.

Интегралдың тұрақты шамасы С₁ анықтайық. Иілу тақырыбында қарастырғандай dy/dx туындысы серпімді сызыққа жүргізілген жанаманың х өсіне қарағандағы бұрышын көрсетеді, ал стерженнің ортасына жүрг.жанама бұл өске пареллель, олай болса x=(l/2)dy/dx туындысы нөлге тең. Сонымен, С₁=0.

Тағы да бір рет интегралдайы

EI_miny = F_crfl²/П²sin(П/l)x+C₂.

Тіректердегі иілу шамасы 0-ге тең болғандықтан, яғни x=0, x=l болғанда, y=0, олай болса С₂ =0.

x=l/2 болғанда, иілу шамасы y=f, бұл дегеніміз

EI_miny = F­_crfl²/П²,

немесе

F_cr=П²EI­­_min/l².

Бұл өрнек топсалы қостіректі бекітілген стерженьге арналған дағдарыс күшті анықтайтын Эйлер формуласы деп аталады.

6- билет

1. Сұрақ

Созылған (сығылған) білеуді беріктікке есептеу. Машиналар мен құрылымдарды және олардың элементтерін жобалағанда, негізінен келесідей үш есептің түрлерімен кездесуге болады: 1) Жобалау есебі, яғни берілген күштердің шамасына сәйкес, таңдап алынған материалдан жасалынатын конструкция элементінің беріктігін, қатаңдығы мен жеткілікті тӛзімділігін қамтамасыз ететін қиманың ең аз ӛлшемдерін анықтау. 2) Беріктікті тексеру есебі, яғни белгілі күштердің шамасы мен конструкция элементтерінің кӛлденең қима ӛдшемдері бойынша элементтердегі нақтылы кернеулердің ең үлкен шамасын анықтап, мүмкіндік кернеумен салыстыру. 3) Жүк кӛтеру қабілетін анықтау есебі, яғни белгілі конструкция элементтерінің кӛлденең қима ӛлшемдері мен материалдарының мүмкіндік кернеуі бойынша конструкция элементтерінің жүк кӛтеру қабілетін анықтау. Созылу мен сығылу деформацияның беріктік шарты келесі формуламен өрнектеледі.

Созылу деформациясымен шынжырларды, арқандарды, болттарды, әр

түрлі аспаларды есептеуде кездессек, сығылу деформациясы іргетастар мен

тіректерді есептеуде қарастырылады.

Білеуге әсер етуші күштерді созушы күштер деп қарастырсақ, (I.2.8, b -

сурет) онда білеудің ұзындығы

(I.2.6)

шамасына ұзарады (созылады), ал ені

b b₁ b₀ (I.2.7)

шамасына қысқарады (сығылады).

Білеудің бастапқы ұзындығының ұзару шамасын - абсолют ұзару, ал

енінің қысқару шамасын b - абсолют қысқару деп атаймыз.

=5<5A5 b шамалары бойынша білеудің деформациялану қабілетін

сипаттауға болмайды, ӛйткені абсолют ұзару мен қысқару білеуге әсер етуші күшпен қатар білеудің бастапқы ӛлшем бірліктеріне байланысты. Сондықтан созылған немесе сығылған білеудің деформациялану шамасын сипаттау үшін, абсолют ұзарудың білеудің алғашқы ұзындығына, ал абсолют қысқарудың білеудің алғашқы еніне қатынастарын алған дұрыс, яғни

мұндағы E- бойлық салыстырмалы деформациясы деп, ал E’- ендік салыстырмалы деформация деп аталады. формулаларынан E мен E’ ӛлшем бірліксіз шамалар екенін көреміз

Деформациялар. Қандай дене болмасын сыртқы күш әсерінен ӛздерінің ӛлшемдері мен пішіндерін ӛзгертеді, яғни деформацияланады, ақырында күштің бір жеткілікті үлкен шамасында қирайды, бірнеше бӛлшектерге бӛлінеді. Денелердің ӛлшемдері мен пішіндерінің ӛзгеруін деформация деп атайды. Ол материалдың атомдарының ара қашықтықтарының ӛзгеруі мен атом блоктарының орын ауыстыруы салдарынан туындайды.

Сыртқы күш әсері жойылғанда, денедегі деформация да жойылса, ондай деформацияны серпімді деформация деп атайды, ал дененің күш әсері

ДЕФОРМАЦИЯ МЕН ОРЫН АУЫСТЫРУ

Қандай дене болмасын сыртқы күш әсерінен өздерінің өлшемдері мен формаларын өзгертеді, деформацияланады.

Дененің сызықты өлшемдерінің өзгеруі сызықтық деформация, ал бұрыштық өлшемдерінің өзгеруі бұрыштық деформация делінеді.

Деформация нәтижесінде дененің сызықтық өлшемінің өcyi – созылу (ұзару), ал кемуі – сығылу (қысқару) деп аталады.

Деформация материалдың атомдарының ара қашықтықтарының өзгеруі мен атом блоктарының орын ауыстыруы салдарынан туады. Оның табиғатын толық зерттеп білу үшін, жазық дененің кез келген нүктесінің жанынан өзара перпендикуляр АВ, СA түзулерін алайық (I. 3, а-сурет).

Дене деформацияланғанда АС түзу сызығы шамасына ұзарады (I. 3, б-сурет). Оның орташа сызықтық салыстырмалы деформациясы келесі формуламен анықталады.

(1.01)

1.3-сурет

Бұл қатынастың бөліміндегі АС кесіндісінің ұзындығы нөлге ұмтылғандағы шегі, А нүктесіндегі толық салыстырмалы деформацияны аныктайды

. (1.02)

Енді бұрыштық деформацияны қарастырайық. Деформацияға дейінгі ВАС тікбұрышы мен деформациядан кейінгі В'А'С сүйір бұрышының арасындағы айырма берілген нүктенің бұрыштық деформациясын сипаттайды.

Сонымен күш түскен дененің кез келген нүктедегі деформациясы сызықтық салыстырмалы және бұрыштық деформациялармен сипатталады. Денеде пайда болған сызықтық және бұрыштық деформациялар сырттан әсер етуші күш жойылғанда толық жойылуы немесе жойылмауы да мұмкін. Сыртқы күш әсері жойылғанда, денедегі деформация да жойылса, ондай деформацияны серпімді деп, ал деформация толық жойылмай қалса, онда қалдық деформацияны пластикалық деформация деп атайды. Егер дененің бекіту шарттары мен нүктелеріндегі деформацияның шамасы белгілі болса, онда кез келген нүктенің деформациядан кейінгі орнын, яғни орын ауыстыру шамасын анықтауға болады. Машина бөлшектері серпімді деформацияланғанда ғана, олардың жұмыс істеу қабілеті қамтамасыз етіледі. Сондықтан, нүктелердің ең үлкен орын ауыстыру шамасы белгілі бip мүмкіндік шамадан аспауы керек. Мұндай шарт теңсіздік ретінде көрсетіліп, қатаңдық шарты деп аталады.

2. Сұрақ

Еркінжазықкүштержүйесі. Жазықпараллелькүштержүйесі. Күштіберілгеннүктегекелтіру.

денеге әсер ететін кез келген күшті дененің қандай да бір нүктесіне өзіне-өзі параллель көшіруге болады, бұл жағдайда келтіру нүктесіне күшпен қатар моменті берілген күштің жаңа түсіру нүктесіне қатысты моментіне тең қос күшті қосу қажет.

Осы сияқты күштің орнын ауыстыруды күшті берілген нүктеге келтіру деп атайды

Әсер сызықтары бір жазықта жататын және параллель болатын күштер жиынын жазық параллель күштер жиыны деп айтады. Физика курсынан белгілідей (I.1.24, а - сурет) бір бағытталған екі параллель күштің тең әсерлі күші берілген күштер қосындысына тең де, осы күштерге параллель және бағыттас болады, ал оның әсер сызығы берілген екі күштің түсу нүктелерін қосатын кесіндіні сол күштердің модульдеріне кері пропорционал болатындай етіп екі бөлікке іштей бөлетін нүктеден өтеді, яғни

(,F1,F2) F1|| F2 ,F1≠ F2 ,R= F1+F2 ,F1/F2=BC/AC .

Еркін жазық күштер жүйесін берілген нүктеге келтіру.

денеге әсер ететін кез келген күшті дененің қандай да бір нүктесіне өзіне-өзі параллель көшіруге болады, бұл жағдайда келтіру нүктесіне күшпен қатар моменті берілген күштің жаңа түсіру нүктесіне қатысты моментіне тең қос күшті қосу қажет.

Осы сияқты күштің орнын ауыстыруды күшті берілген нүктеге келтіру деп атайды,

7- билет

1. Сұрақ

Қос күштерді қосу.

Қос күштердің тепе-теңдік шарты. Теорема.

Денеге бір жазықтықта әсер ететін қос күштер жиыны, моменті қос күштердің моменттерінің алгебралық қосындысына тең болатын қос күшпен тепе-тең.

Сонымен, денеге бір жазықта әсер ететін бірнеше қос күштерді қосу үшін, осы қос күштерінің моменттерінің алгебралық қосындысын анықтаса жеткілікті. Қосу нәтижесінде алынған момент тең әсерлі қос күшті анықтайды.

яғни денеге бір жазықта әсер етуші қос күштер жиыныі тепе-теңдікте болу үшін жиындағыі қос күштер моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті.

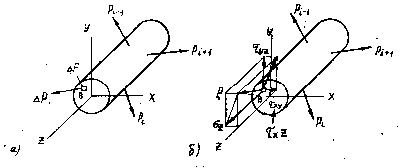Ішкі күштер дененің бір бөлігімен екінші бөлігіне көлденең қима арқылы үздіксіз жайыла таралып беріледі Олардың әсер ету заңдылығын білу үшін қима бетінде жатқан нүктесін қарастырайық (1.5, а-сурет). Нүктені қоршаған шексіз кіші ауданды , ал ол ауданға сәйкес келетін ішкі күшті деп белгілейік. Ішкі күш ның шексіз кіші аудан ке қатынасы

1.5-сурет

нүктесіндегі ішкі күштің орташа шамасын – орташа кернеуді аңықтайды.

. (1.04)

Шексіз кіші аудан нөлге ұмтылғандағы көрсетілген қатынастың шегі В нүктесіндегі толық кернеу деп аталады:

. (1.05)

Толық кернеудің көлденең қима жазықтығына перпендикуляр OZ өсте, түсіріген проекциясы тік кернеу деп аталып, OZ әрпімен белгіленеді, ал қима бетіне түcipiлгeн проекциясы жанама кернеу деп

1.6-сурет

аталып, әрпімен белгіленеді (1.5, б-сурет).

Суреттен, толық кернеу , екендігін көреміз.

2. Сұрақ

Ясинский формуласы. Іс жүзінде, кӛптеген конструкция элементтері иілгіштігі шектік мәннен кем стержень болып келеді. Мұндай стержендерді орнықтылыққа есептеудің басқа әдісін Ф.С. Ясинский ұсынды. Алдын-ала кӛптеген зерттеулердің нәтижелерін талдап және кӛптеген материалдардың ау 

мен 0@0AK=40“K BÙC5;4V;V:BV AK710H0 :5A:V=45?, ?@>?>@F8>=0;4K› H5:B5= үлкен дағдарыс кернеулерді анықтайтын келесі эмпирикалық формуланы қорытып шығарды

мұндағы a,b - материалдарға байланысты, тәжірибе жүзінде анықталатын,

қабылданатын тұрақты коэффициенттер. Бұл формуланы Ясин формуласы деп

атайды. Кейбір материалдар үшін, a,b коэффициенттері 2.1-кестеде берілген.

8- билет

1. Сұрақ

«Материалдар кедергісі» деп машина мен конструкциялардың бөліктерінің беріктігі, қатаңдығы және орнықтылығы туралы ғылымды айтамыз.

Беріктік деп конструкцияның немесе оның жеке элементтерінің сыртқы күш әсеріне қирамай қарсыласу қабілетін айтады.

Қатаңдық деп конструкция мен оның элементтерінің деформацияға қарсыласу қабілетін атайды.

Орнықтылық деп конструкцияның немесе оның элементтерінің белгілі алғашқы серпімді тепе-теңдік күйін сақтау қабілетін айтады. Есептеу денелерінің түрлері. Инженерлік практикада кездесетін сан алуан конструкция элементтері пішіндері мен ӛлшемдеріне байланысты жинақталып, тӛмендегідей қарапайым түрлерге жіктелген: 1 Білеу (брус) - екі ӛлшемі үшін,шісінен әлдеқайда кіші дене (I.2.1, а, b - сурет). Дербес жағдайда білеудің кӛлденең қимасының ауданы тұрақты, ал ӛсі түзу сызықты болуы мүмкін (I.2,1, b - сурет).

Ӛсі түзу сызықты білеуді стержень деп атайды. Білеудің өсі дегеніміз кӛлденең қималардың ауырлық центрлерінің геометриялық орны (I.2.1, c - сурет). 2 Пластина – ара қашықтығы басқа ӛлшемдеріне қарағанда ӛте кіші, екі жазық бетпен шектелген дене (I.2.2, а - сурет). 3 Қабықша - ара қашықтығы басқа ӛлшемдеріне қарағанда әлдеқайда кіші болатын екі қисық сызықты беттермен шектелген дене (I.2.2, b - сурет).

4 Массив - үш ӛлшемдері ӛзара шамалас дене (I.2.2, с - сурет). «Материалдар кедергісі» пәнінде қатаңдығы жеткілікті, аз деформацияланатын, кӛбінесе кӛлденең қималары тұрақты, білеу тәріздес жұмыр денелер немесе олардан құрылған қарапайым жүйелер қарастырылады.

Сыртқы күштер және олардың сұрыптамасы, түрлері.

Сыртқы күштер. Материалдар кедергісі есептерін шешкенде, ең алдымен конструкция элементтеріне әсер ететін сыртқы күштің шамасы мен түсу сипатын анықтап алу қажет. Белгілідей, сыртқы күш деп денелердің бір- бірімен әсерін, демек, сол конструкция элементтерінің өзара әсерін де айтады. Сол сияқты берілген конструкция элементінің басқа денемен әсері қарастырылған элемент үшін, сыртқы күш болып табылады. Мысалы, шамға құйылған жермайдың салмағы шан орнатылған тұғырға түседі, одан тұғырдың аяқтары арқылы іргетасқа түседі. Элементтің өз салмағы да сыртқы күшке жатады.

Сыртқы күштер көлемдік және беттік болып бөлінеді. Беті арқылы берілетін сыртқы күшбеттік, ал көлемі арқылы берілетін сыртқы күш көлемдік күш деп аталады.

Беттік күштер қадалғаннемесе таралған күш болуы мүмкін.

Қадалған күш деп, конструкция элементтеріне өз өлшемдерімен салыстырғанда өте шағын аудан арқылы берілетін күшті айтады. Қадалған күштің өлшем бірлігі ньютон (Н), килоньютон (кН), меганьютон (МН). Мысалы, тісті берілістегі тістердің бір-біріне әсері. Ауданның өте шағындығына байланысты қадалған күш әдетте денеге нүкте арқылы беріледі деп есептелінеді.

Таралған күш деп не элементтің барлық көлеміне (көлемдік күш), не белгілі бір ауданына (жазықтық күш), не белгілі бір ұзындыққа (сызықтық немесе бойлық жүк) үздіксіз түсірілген күшті айтады. Ол қарқындылығымен сипатталады. Қарқындылық деп күштің бірлік көлемге немесе бірлік ауданға немесе бірлік ұзындыққа түсірілген шамасын айтады. Қарқындылық латынша q әрпімен белгіленеді, сәйкесінше таралған күштердің өлшем бірлігі: көлемдік күш - ; жазықтық күш - ; , ;сызықтық немесе бойлық күш - ; ,

Бұл күштер таралу заңдылықтарына байланысты біркелкі таралған тұрақты және бірқалыпсыз таралған айнымалы күштер деп жіктеледі. Біркелкі таралған тұрақты күштің кез келген нүктедегі қарқындылығы өзара тең, ал бірқалыпсыз таралған айнымалы күштің қарқындылығы әр түрлі.

Денеге тұтас көлемі арқылы берілетін күштер қатаң түрде үздіксіз біркелкі тараған деп қарастырылады.

Көлемдік күшке мысал ретінде дененің салмағын, жазықтық күшке – будың қазан қабырғасына қысымын, сызықтық күшке – ені ұзындығынан өте аз арқалыққа ұзына бойлы түсірілген күшті келтіруге болады.

Сыртқы күш әсер ететін уақытына байланысты да екі топқа бөлінеді: тұрақты күшжәне уақытша күш.

Тұрақты күш деп мөлшері мен бағыты өзгермейтін күшті айтады. Егер денеге түскен күштердің шамасы немесе бағыты уақытқа байланысты өзгеріп отырса, ондай күштерді айнымалы күштер деп атайды.

Сыртқы күштерді статикалық және динамикалықкүштер деп те топтастыруға болады.

Статикалық күш деп өзінің шамасын немесе түсу нүктесін баяу жылдамдықпен өзгертетін, осы жағдайда туындауы мүмкін үдеуді ескермеуге болатын күшті атайды. Мұндай күш әсерінен конструкцияның және оның элементтерінің тербелісі мардымсыз аз болады.

Динамикалық күш деп уақытқа байланысты үлкен жылдамдықпен өзгеретін күшті айтады. Мұндай күштің әсерінен конструкция немесе оның элементтері елеулі тербелістерге ұшырайды. Тербеліс жылдамдығының өзгеруіне байланысты конструкцияда пайда болатын, оның массасы мен үдеуінің көбейтіндісіне тура пропорционал екпін күші шамасы жағынан конструкцияда тербеліс тудырушы сыртқы күштің шамасынан бірнеше есе үлкен болуы мүмкін.

Динамикалық күштер соққы, айнымалы–қайталанбалы және т. б. түрлерге жіктеледі.

Соққы күш деп кинетикалық энергиясы бар қозғалыстағы дененің екінші бір денеге соқтығысуы арқылы берілетін күшті айтады.

Айнымалы–қайталанбалыкүштер деп машина бөлшектеріне уақытқа тәуелді, периодты түрде қайталанып түсетін күштерді атайды. Мысалы, қозғалыстағы машинаның шатун, білік сияқты бөліктеріне немесе темір жол вагонының өсіне түсетін күштер айнымалы – қайталанбалы күштерге жатады.

Жалпы жағдайда күш уақытқа тәуелді күрделі заңдылықпен өзгеруі мүмкін.

2. Сұрақ

Күштің өске проекциясы. Белгілі бағытталған түзу сызықты өс деп атайды. Күштің өске проекциясы деп, күш векторының ұштарынан өске түсірілген екі перпендикулярмен шектелген, өстің бағытталған кесіндісі аталады. Егер кесінді бағыты өстің оң бағытымен сәйкес келсе, күштің өске проекциясы оң таңбалы деп есептеледі. Егер кесінді бағыты өстің оң бағытына қарама-қарсы болса, күштің өске проекциясы теріс таңбалы делінеді

Сонымен, күштің өске проекиясының шамасы осы күштің модулін өстің оң бағыты мен күштің бағыты арасындағы бұрыш косинусына көбейткенге тең.

9- билет

1. Сұрақ