1. Вероятностные распределения. Случайная величина. Дискретные и непрерывные случайные величины. Примеры.

ВР - если вы имеете некоторую переменную, принимающую значения случайным образом, то вам хотелось бы знать, с какими вероятностями эта переменная принимает определенные значения. Совокупность этих вероятностей как раз и задает распределение вероятностей

СВ - это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.

Дискретные величины – описываются биноминальным распределением(величина может принимать только два значения)мужчины и женщины

2. Числовые характеристики случайной величины.

Мат.ожидание, дисперсия,

Математическое ожидание для дискретной случайной величины.

Мат.ожид. – среднее значение М(х)= Σ Р(х)

Свойства математического ожидания для постоянной величины.

1) Математическое ожидание постоянной величины равно самой постоянной.

2) Постоянный множитель можно выносить за знак математического ожидания

3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых.

3. Дисперсия постоянной случайной величины и ее свойства.

D(x)= Σ(-M(x))²P(x)

1) Дисперсия постоянной величины равна нулю.

2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.

3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин

4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.

4. Биноминальное распределение. Схема Бернулли и условия ее воплощения. Расчет среднего значения и дисперсии при биноминальном распределении.

Результат случ.исхода описывается в 2х исходах.

Дисперсия определяет насколько случайные величины отклоняются от среднего значения – мера рассеяния случ.величины относительно среднего.

М=np, D²⁼npq

5. Распределение Пуассона. Расчет вероятности распределения Пуассона. Особенности распределения Пуассона по сравнению с биноминальным распределением.

Распределение дискретной случайной величины, равной числу успехов в определенных интервалах.

Позволяет проявить число появлений в опред. Интервале. Случайная величина х (которая определяет успехи )может принимать неограниченное кол-во значений. Успехи случайны независимы, распределены равномерно, внутри некоторого интервала.

Р(х)= М^хе^-М/х!

• Биноминальное распределение определяется средним кол-вом испытаний n с вероятностью, в то время , как распределение Пуассона только М(средним)

• В первом случае число испытаний ограничено(n) во втором - бесконечно.

6. Характеристики нормального распределения. Свойства графика плотности нормального распределения. Примеры построения графиков для разных случайных величин.

Непрерывная Случайная величина имеет нормальное распределение если её плотность задается уравнением:

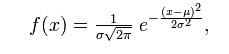
Имеет форму колокола, симметричного относительно М