13. Уравнение неразрывности (в дифференциальной форме)
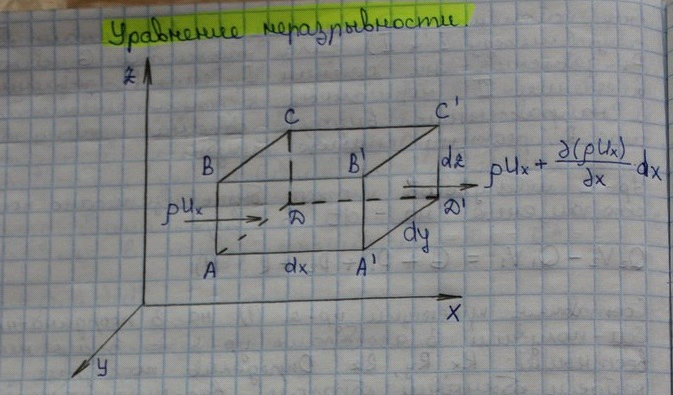
На рисунке показана схема течения потока через стенки элементарного параллелепипеда. Изолируем неподвижный объём в форме параллелепипеда со стороны dx dy dz. Обозначим через Ux составляющую скорости течения жидкости вдоль Ox Uy вдоль OY и Ur вдоль OZ. Через площадку ABCD за время dt внутрь параллелепипеда втекает масса жидкости pUxdydzdt. Из объёма параллелепипеда в течении времени dt через площадку A'B'C'D' вытекает масса жидкости pUxdydzdt+ (pUx)dxdydzdt
При течении жидкости должны соблюдаться условия сплошности заключающие в том, что жидкость или газ должны двигаться в трубопроводах или воздуховодах как сплошная среда без разрывов.
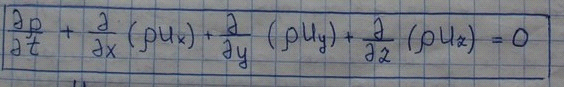
14. Метод анализа размерности (пи-теорема)
ПИ - теорема - это зависимость между некоторыми физическими величинами, всегда может быть преобразована в уравнение в которое войдут безразмерные комбинации тех же физических величин( числа пи) при чём число этих безразмерных комбинаций всегда меньше чем число исходных физических величин.
В соответствии с ПИ-теоремой уравнение можно записать в виде: Ф(ПИ1,ПИ2...ПИn)=0 Где ПИ независимая безразмерная произведение нескольких А.
При этом заметим, что число членов в физическом уравнение сократилось от n до n-m. В задачах механики жидкости имеется 44 первичных (основных) размерности это масса (М), длина (L), время (Т). В этом случая max число независимых комбинаций можно получить выражая числа ПИ в виде:
ПИ1=А1х1*А2у1*А3z1*А4
ПИ2=А2х2*А2у2*А3Z2*А5
В каждом числе будет (m+1) переменная
15. Движение газа в трубе переменного сечения. Сопло Лаваля.
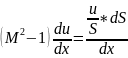
Это уравнение позволяет провести качественный анализ характера движения сжимаемого газа в трубе переменного сечения.
Рассмотрим
движение при М<1,
т.е. при дозвуковом потоке. В этом случае
М2-1<0
и знак
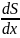будет зависеть от знака производной
скоростей
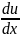. В сужающемся канале (конфузоре)
скорость растет, а в расширяющемся
канале (диффузоре) скорость убывает.
При числах М>1, т.е. при сверхзвуковом потоке газа имеем М2-1>0, в сужающейся трубе скорость убывает, а в расширяющейся растет.
Е
сли
скорость на входе дозвуковая, то возможны
2 случая (кривые 1 и 2). В первом случае
скорость в узком сечении не достигает
скорости звука. Тогда в расширяющейся
части скорость будет убывать и на выходе
из сопла будет дозвуковой.
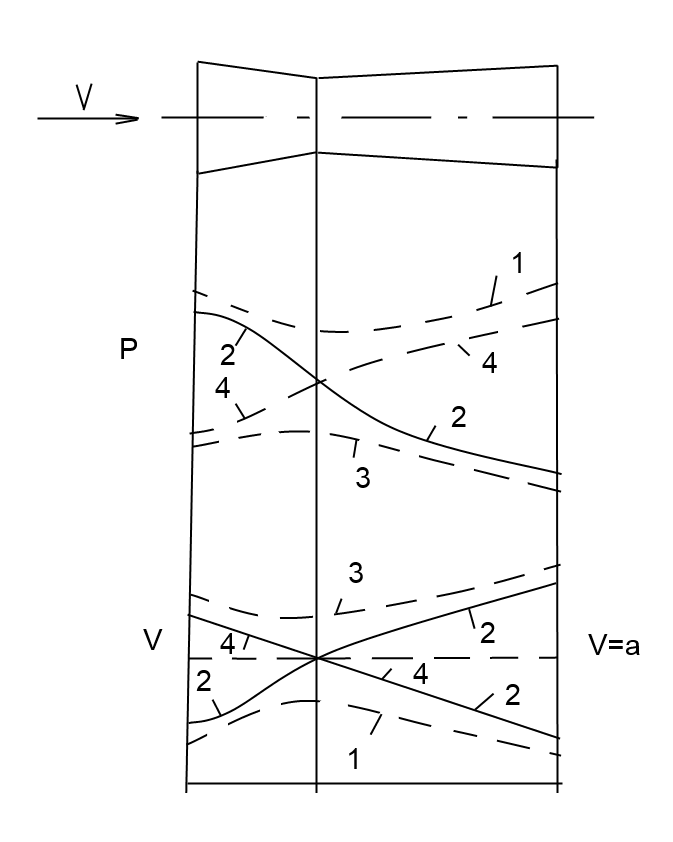
Во втором случае (кривая 2 и и 2') скорость в наиболее узком сечении будет достигать скорости звука и в зависимости от величины давления за соплом либо дальше в расширяющейся части трубы, становится сверхзвуковой (кривая 2), либо если давление на выходе из трубы сверхкритическое, скорость в диффузоре убывает и при выходе из трубы становится дозвуковой (кривая 2')
Труба переменного сечения, рассчитанная так, что дозвуковая скорость на входе становится сверхзвуковой на выходе, называется соплом Лаваля. Наиболее узкое сечение называют критическим, а соответствующие параметры потока также называют критическими(скорость, давление, плотность, температура)
Если скорость на входе сверхзвуковая, то убывая в сужающейся трубе она достигает наименьшего значения в наиболее узком сечении. Если это наименьшее значение остается больше скорости звука, то в расширяющейся части трубы скорость газа растет и на выходе будет также, как и на входе сверхзвуковой (кривая 3)
Когда сверхзвуковой поток достигает в наименьшем сечении скорости звука ( кривая 4), то так же, как и для кривой 2, возможны 2 варианта. Если давление на выходе меньше критического, то в диффузоре скорость будет расти и на выходе она станет сверхзвуковой (кривая 2). При давлении больше критического скорость в диффузоре убывает и на выходе она достигает дозвуковой (кривая 2')