
Экономика энергетики / энергетика-лк
.6.doc
Лекция 6. Тема 3. Методы преобразования энергии.
3.6. Газотурбинный цикл Брайтона.
В этом разделе рассматривается (упрощенно) один из реальных циклов, распространенных в энергетике, авиации, в судовых установках, на железнодорожном транспорте. В газотурбинных циклах рабочим телом является газ. Обычно это воздух или продукты сгорания топлива. В ядерной энергетике перспективным рабочим телом рассматривается гелий.
Наиболее просто нагревать и охлаждать газ при постоянном давлении (изобарически), например, нагревая или охлаждая трубы, по которым течет газ.




 2
4 5
2
4 5


 3
3



 1
1








6





 Т
1
p Q1
Т
1
p Q1


 4
1
4
1
 Q1
Q1
 2
2
 4
4


 3
2
3
2
Q2 Q2
3


S V
Рис.3.9. Тепловая схема, TS-диаграмма и pV-диаграмма газотурбинного цикла Брайтона.
Согласно тепловой схеме (рис.3.9) газ нагревается изобарически (процесс 4-1 на диаграммах) в теплообменнике 1 (в ядерном реакторе, камере сгорания и т.п.). Нагретый газ адиабатически расширяется в газовой турбине 2 (процесс 1-2), расположенной на одном валу 3 с компрессором 4, в котором газ сжимается адиабатически (процесс 3-4) после охлаждения (изобарического) в холодильнике 6 (процесс 2-3). Вращательное движение, приобретенное турбиной при расширении газа, передается ротору электрогенератора 5, где механическая энергия преобразуется в электрическую.
Следует отметить, что турбины, впервые созданные в 1890 г., стали основным средством получения электроэнергии и основным типом судовых и авиационных двигателей.
Оценим КПД цикла Брайтона как функцию максимальной Т1 и минимальной Т3 температур и максимального р1 и минимального р2 давлений в цикле. Согласно первому началу термодинамики (3.5), определению работы расширения (3.3) и свойству дифференциалов d(pV)=pdV+Vdp имеем
dQ=dU+dA=dU+pdV=dU+d(pV) – Vdp=di - Vdp. (3.14)
Здесь величина i=U+pV носит наименование энтальпии или теплосодержания единицы массы рабочего тела (Дж/кг), а величина (-Vdp) имеет смысл полезной внешней работы. Из полученного выражения следует, что в изобарическом процессе (dp=0) полезной внешней работы не совершается и все тепло, подведенное к телу, идет на увеличение его теплосодержания (энтальпии) dQ=di. Для однофазного вещества (газа, жидкости или твердого тела) увеличение теплосодержания сопровождается увеличением температуры тела Т: dQ=di=СpdT, здесь Сp – теплоемкость вещества, Дж/кг.град, численно равная количеству тепла (Дж), которое надо подвести к единице массы вещества (кг), чтобы нагреть его на один градус. Данные о теплоемкости газов и других веществ содержатся в таблицах теплофизических свойств веществ (см.табл.3.2).
Таким образом, для цикла Брайтона количества тепла, полученного от нагревателя и отданного в окружающую среду, равны:
Q1= Сp(T1 - T4), Q2= Сp(T2 – T3). (3.15).
Подстановка этих выражений в (3.2) или (3.12) дает величину КПД. Однако, температуры Т2 и Т4 зависят от давлений газа в нагревателе (р1) и холодильнике (р2). Найдем эти зависимости, используя свойства адиабатического процесса (dQ=0) в турбине и в компрессоре. Согласно уравнению первого начала (3.14) для адиабаты имеем: 0=di-Vdp или (-Vdp)=-di. Как видно, полезная внешняя работа (-Vdp) совершается за счет убыли энетальпии (теплосодержания) рабочего тела. Поскольку di= CpdT, то
CpdT=Vdp. (3.16)
Давление, температура и объем газа связаны уравнением состояния (идеальных газов)
рV=RT или p= RT, (3.17)
где =1/V – плотность газа, кг/м3, R=Ro/ - газовая постоянная, Ro=831 Дж/моль.град – универсальная газовая постоянная, одинаковая для всех газов, - молекулярная масса (масса одного моля) газа, кг/моль, (см. табл.3.2).
Таблица 3.2.
Теплофизические свойства некоторых веществ при нормальных условиях
(комнатная температура и атмосферное давление)
|
Вещество |
Молекулярная масса , кг/моль |
Плотность , кг/м3 |
Теплоемкость Ср, Дж/кг.град |
Теплопроводность , Вт/м.град |
|
Водород, Н2 |
2 |
0,09 |
14300 |
0,17 |
|
Гелий, Не |
4 |
0,18 |
5200 |
0,14 |
|
Кислород, О2 |
32 |
1,43 |
925 |
0,025 |
|
Углекислый газ, СО2 |
44 |
1,8 |
871 |
0,014 |
|
Воздух |
|
1,2 |
1000 |
0,026 |
|
Вода, H2O |
18 |
998 |
4183 |
0,6 |
|
Железо, Fe |
56 |
7900 |
462 |
74 |
|
Медь, Cu |
63 |
8800 |
381 |
384 |
В![]() ыражая
удельный объем газа через давление и
тепературу с помощью уравнения состояния
получим V=RT/p.
Подставляя это выражение в формулу
(3.16) первого начала для адиабаты, получаем
дифференциальное уравнение адиабаты
в разделяющихся переменных (р,Т):
ыражая
удельный объем газа через давление и
тепературу с помощью уравнения состояния
получим V=RT/p.
Подставляя это выражение в формулу
(3.16) первого начала для адиабаты, получаем
дифференциальное уравнение адиабаты
в разделяющихся переменных (р,Т):
Р![]() ешение
этого уравнения, проходящее через
некоторую точку (ро,То),
имеет вид
ешение
этого уравнения, проходящее через
некоторую точку (ро,То),
имеет вид
Вернемся теперь к циклу Брайтона (рис.3.9). Отношение максимального давления в цикле (р1=р4) к минимальному (р2=р3) принято обозначать греческой буквой (степень сжатия газа в компрессоре или степень расширения в турбине): = р1/ р2= р4/ р3. Из (3.19) следует, что отношение температур в турбине и в компрессоре, где идут адиабатические процессы, одинаковы и равны
![]()
В итоге для КПД цикла Брайтона получаем выражение
![]()
Как видно, КПД цикла Брайтона не зависит от уровня температур (явно), а только от степени расширения газа в турбине . При =1 имеем =0. Величина R/Cp для одноатомных газов (гелий, аргон и др.) равна 2/5=0,4, для двухатомных газов (водород, кислород, азот и др.) 2/7=0,29, для многоатомных газов (воздух, продукты сгорания) менее 0,2. Как следует из рис.3.10, КПД цикла Брайтона не превышает 50% при 5, в то время как КПД цикла Карно при Тмакс=727оС и Тмин=27оС составляет 70%.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
4 |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
0,2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 1 2 3 4 5 6 7 8 9
Рис.3.10. Зависимость КПД газотурбинного цикла от степени расширения газа в турбине: 1-цикл Брайтона для одноатомного газа, 2-цикл Брайтона для двухатомного газа, 3- газотурбинный цикл с идеальной регенерацией тепла при Тмакс=727оС и Тмин=27оС, 4-газотурбинный цикл с регенерацией тепла при Тмакс=727оС и Тмин=27оС (при степени регенерации 90%, КПД турбины и компрессора 90%).
Как повысить КПД цикла Брайтона? Из TS-диаграммы на рис.3.9 следует, что если температура газа на выходе из турбины Т2 превышает температуру газа на выходе из компрессора Т4, то возможна регенерация тепла в цикле. Для увеличения доли тепла, регенерируемого в цикле, выгодно понижать температуру Т4. Достигается это путем многоступенчатого сжатия газа с промежуточным охлаждением после каждой ступени. Такая схема изображена на рис.3.11. Оптимальная степень расширения газа в этом случае находится в диапазоне =2-4 (см.рис.3.10).


 2
3 4
5
2
3 4
5














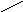

 1
6 7
1
6 7














 8
8



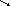

 1
1
 Q1
Q1


 6 2
6 2


 Регенерация
Регенерация





 5
3
5
3


 4
Q2
4
Q2

Рис.3.11. Тепловая схема и TS-диаграмма газотурбинного цикла с регенерацией тепла и двухступенчатым сжатием и промежуточным охлаждением газа. На тепловой схеме: 1-источник тепла (нагреватель), 2-газовая турбина, 3-компрессор низкого давления, 4-компрессор высокого давления, 5-электрогенератор, 6,7-промежуточные холодильники, 8-регенератор-теплообенник. На TS-диаграмме: 1-2 –адиабатическое расширение в турбине, 2-3 – изобарическое охлаждение в регенераторе, 3-4-5 – многоступенчатое охлаждение и сжатие газа в компрессоре, 5-6 – изобарический нагрев газа в регенераторе, 6-1 – изобарический нагрев во внешнем нагревателе
3.7. Паротурбинный цикл Рэнкина.
Тепловая схема такого цикла приведена на рис.3.2. Рабочим телом цикла Рэнкина является вода и водяной пар. Для анализа TS-диаграммы цикла Рэнкина необходимо обратиться к термодинамическим свойствам воды и ее пара.
3.7.1. Термодинамические свойства воды и водяного пара. Вначале введем понятия гомогенной и гетерогенной термодинамических систем. Система гомогенна, если ее химический состав и физические свойства всюду одинаковы или непрерывно (без скачков) изменяются от точки к точке. Система гетерогенна, если она состоит из двух или более различных гомогенных систем. Гомогенные области в гетерогенной системе называются фазами. Чистая вода или сухой пар являются гомогенными системами. Пример гетерогенной системы – смесь пара с капельками воды или смесь воды с пузырьками пара.
Следующим важным понятием термодинамики является равновесие фаз. Вода и пар находятся в равновесии, когда нет преимущественного испарения воды или конденсации пара.
?
3.8. Минимальная стоимость и оптимальный КПД космической энергоустановки.
Когда говорят о «Глобализации экономики», об «Электронном бизнесе» и об «Информационном обществе», то не всегда ясно представляют масштабы технических средств для обеспечения телекоммуникаций. Невозможно представить себе всемирную связь без спутниковых систем ретрансляции, способных десятилетиями работать в космических условиях без вмешательства человека. При потребностях электропитания таких спутников около 100 кВт наиболее перспективны ядерные энергетические установки с компактными реакторами-преобразователями (термоэмиссионные или термоэлектрические преобразователи). Схеа такой учтановки показана на рис. 3.___.

 4
4






 1
2 3
1
2 3








 5
5



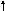


 6
6
6
6







7
Рис.3.___. Схема космической ядерной энергетической установки с прямым преобразованием тепла в электричество: 1-ядерный реактор с термоэмиссионным или термоэлектрическим преобразователем, 2-радиационная защита, 3-блок приборов управления, 4-холодильник-излучатель, теплоноситель, циркулирующий через реактор и излучатель, 6 - трубы с теплоносителем в излучателе (в разрезе), 7 – стенка излучателя (в разрезе).
В предыдущих разделах отмечено, что на промышленных электростанциях большой вклад в стоимость электроэнергии вносят затраты на топливо. Для экономии топлива необходимо увеличивать КПД цикла преобразования энергии. Какие требования предъявляются к КПД космической энергоустановки? Ядерные реакторы могут работать без дозаправки топливом несколько лет. Поэтому снижение стоимости космической энергоустановки достигается путем максимального снижения ее массы (вывод в космос килограмма полезного груза по стоимости близок к стоимости килограмма золота).
В космосе избыточное тепло цикла Q2 может быть сброшено в окружающую среду (в космическое пространство) тепловым излучением. Интенсивность теплового излучения согласно закону Стефана-Больцмана пропорциональна четвертой степени температуры холодильника-излучателя Т2. То есть мощность теплового излучения Q2 с поверхности холодильника-излучателя, имеющего площадь F м2, равна
Q2=FT4, Вт, (3.___)
Где =5,67.10-8 Вт/м2град4 – постоянная Стефана-Больцмана, - степень черноты поверхности излучателя..
Отсюда следует, что уменьшение нижней (минимальной) температуры цикла Т2, необходимое для повышения термического КПД цикла К=1-Т2/Т1 при заданной температуре Т1 подвода тепла (температуры в реакторе), приводит к резкому увеличению площади излучателя F. С ростом площади излучателя растет и его масса. В установках большой мощности масса излучателя может давать основной вклад в массу всей энергоустановки. Поэтому в качестве целевой функции можно взять отношение генерируемой электрической мощности W=Q1-Q2 к площади поверхности излучателя F (Q1 – тепловая мощность реактора). Величина W/F должна быть максимальна.
КПД энергетической установки =1- Q2/ Q1 представим как произведение термического КПД К=1-Т2/Т1 на внутренний КПД 01, который характеризует необратимость преобразования тепла в электричество (несовершенство реального цикла по сравнению с циклом Карно): =К 0. В таком случае выражение для целевой функции можно получить в виде:
![]()
Верхняя (максимальная) температура цикла Т1 обычно лимитируется термостойкостью материалов и может рассматриваться как неуправляемый (заданный) параметр. В таком случае величина W/F как функция КПД цикла Карно К имеет экстремум. Дифференцируя целевую функцию по К и приравнивая производную нулю, получаем алгебраическое уравнение для определения оптимального значения термического КПД, при котором W/F максимально:
1 - К - 4К(1 - К0) = 0.
В совершенной энергетической установке, в которой внутренний КПД близок к 1 (0=1), оптимальный термический КПД равен К = 25 %, а Т2/Т1=3/4. В несовершенной установке, в которой внутренний КПД мал (0=0), имеем К = 20 %, а Т2/Т1=4/5.




 0,6
0,6


 0,4
0,4