2.Расчет длительности импульса двоичного кода и ширины спектра сигнала

После определения частоты дискретизации и числа разрядов двоичного кода можно определить длительность импульса кодовой последовательности

=

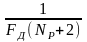
где _с – длительность временного интервала, предназначенного для передачи сигналов синхронизации.

В системах, которые являются предметом настоящей курсовой работы, предусмотрено использование сигналов с активной паузой за счёт изменения фазы на  или частоты на некоторое значение _м. Скачкообразное изменение параметра сигнала называется манипуляцией в отличие от модуляции, которая предусматривает плавное изменение параметра. Таким образом, в результате манипуляции двоичная последовательность кодовых символов с различными фазами ( частотами) может быть представлена суммой двух импульсных последовательностей с различными начальными фазами или частотами. Поскольку характер последовательностей определяется реализацией сообщения, каждую из них следует считать случайным процессом с характерной для последовательности прямоугольных импульсов функцией корреляции в виде гармонической функции (косинуса) с огибающей треугольной формы. Спектральная плотность мощности такой последовательности имеет вид функции (sin² х)/х², максимум которой находится на несущей частоте, а ширина главного лепестка по первым нулям спектральной плотности равна f₀ = 2/_u. На практике и в литературе [1,4,6] обычно ширина спектра определяется полосой частот, в которой сосредоточено 80-90% энергии (мощности) сигнала. По этому критерию для радиоимпульса прямоугольной формы обычно принимается

f_с=F_д(N_P+2)

f_с =

3.Информационные характеристики каналов связи.

1. Энтропия источника сообщений

W₄ (x) = ; ;

2. Информационная насыщенность

Для оценки избыточности сначала рекомендуется рассчитать информационную насыщенность сообщения :

I_Н (х) = Н (х)/Н_МАКС,

где Н_МАКС – максимальная энтропия источника, достигаемая при равномерном распределении.

Н_МАКС = - бит/симв

Тогда избыточность может быть найдена из выражения:

R(х) = 1 – I_Н (х) = .

R(x) = 1-

Производительность источника сообщения находится из равенства:

V_n = бит/с

4.Расчёт отношений мощностей сигнала и помехи, необходимых для обеспечения заданного качества приёма

Пропускная способность канала связи определяется известной формулой Шеннона

С = log

1+

5.Выбор сложного сигнала для передачи информации и синхронизации.

Заметим, что наилучший способ приёма - идеальный приёмник Котельникова – может быть реализован при сигнале, известном точно за исключением, в данном случае, факта: какой из двух возможных сигналов - S₁ (t) или S₂ (t) - присутствует на входе приёмника в данный момент времени. Помехоустойчивость приёмника, характеризуемая вероятностью ошибки р_ош, определяется только отношением его энергии к спектральной плотности помехи. Поэтому применение сложных сигналов не может дать выигрыша помехоустойчивости при помехе в виде широкополосного шума и сигнале, известном точно. Однако применение сложных сигналов позволяет получить целый ряд других преимуществ – повышение помехоустойчивости по отношению к помехам от других подобных систем связи, при действии узкополосных помех, многолучевом распределении сигнала и т.п. Кроме того, использование сложного сигнала позволяет обеспечить синхронизацию устройства восстановления аналогового сообщения по принятому цифровому сигналу.

Таким образом, нужно выбрать два вида используемых сигналов с ФКМ – фазокодовой манипуляцией. Один сигнал должен быть использован для синхронизации, второй – для передачи информационных символов.

Выберем для передачи информационной последовательности код Баркера, для импульсов синхронизации выберем М-последовательность.

D_k=a₁d_k-1+ a₂d_k-2 +…..+a_nd_k-n – М-последовательность

Инф:D_k=d_k-1+d_k-4

Синхр: D_k=d_k-3+d_k-4

Первые четыре импульса задаются в соответствии с вариантом, после пятого задается последовательность. Зададим первые четыре импульса:

d₁d₂d₃d₄

1 1 0 0 ,следующие рассчитаем по формулам:

d₅=d₂+d₁=1+1=0 d₅=d₄+d₁=0+1=1

d₆=d₃+d₂=0+1=1 d₆=d₅+d₂=1+1=0

d₇=d₄+d₃=0+0=0 d₇=d₆+d₃=0+0=0

d₈=d₅+d₄=0+0=0 d₈=d₇+d₄=0+0=0

d₉=d₆+d₅=1+0=1 d₉=d₈+d₅=0+1=1

d₁₀=d₇+d₆=0+1=1 d₁₀=d₉+d₆=1+0=1

d₁₁=d₈+d₇=0+0=0 d₁₁=d₁₀+d₇=1+0=1

d₁₂=d₉+d₈=1+0=1 d₁₂=d₁₁+d₈=1+0=1

d₁₃=d₁₀+d₉=1+1=0 d₁₃=d₁₂+d₉=1+1=0

d₁₄=d₁₁+d₁₀=0+1=1 d₁₄=d₁₃+d₁₀=0+1=1

d₁₅=d₁₂+d₁₁=1+0=0 d₁₅=d₁₄+d₁₁=1+1=0

Синхр. Инф.

110001001101011 110010001111010

По этим данным строим структурную схему согласованного фильтра для информационного сигнала и для синхросигнала.

Структурная схема согласованного фильтра для информационного импульса.

1

12

0

0

1

0

0

0

1

1

1

1

0

1

0

S_вх(t)

-1

-1

-1

-1

-1

-1

-1

Σ

S_вых(t)

СФОИ

Структурная схема согласованного фильтра для синхросигнала

1

12

0

0

0

1

0

0

1

1

0

1

0

1

1 1

-1

СФОИ

S_вх(t)

-1

Σ

S_вых(t)

Строим функцию корреляции для информационного сигнала.

Вход	0	1	0	1	1	1	1	0	0	0	1	0	0	1	1
	0	1	0	1	1	1	1	0	0	0	1	0	0	1	1
		0	0	1	1	1	1	0	0	0	1	0	0	1	1
*			1	0	1	0	0	0	0	1	1	1	0	1	1
*				1	0	1	0	0	0	0	1	1	1	0	1
					0	1	0	1	1	1	1	0	0	0	1
*						1	0	1	0	0	0	0	1	1	1
*							1	0	1	0	0	0	0	1	1
*								1	0	1	0	0	0	0	1
									0	1	0	1	1	1	1
										0	1	0	1	1	1
											0	1	0	1	1
												0	1	0	1
*													1	0	1
														0	1
*															1
	-1	0	1	0	1	4	-1	0	-5	-2	-1	-2	-1	0	15

Строим функцию корреляции для синхросигнала

Вход	1	1	0	1	0	1	1	0	0	1	0	0	0	1	1
	1	1	0	1	0	1	1	0	0	1	0	0	0	1	1
		1	1	0	1	0	1	1	0	0	1	0	0	0	1
*			0	0	1	0	1	0	0	1	1	0	1	1	1
*				0	0	1	0	1	0	0	1	1	0	1	1
*					0	0	1	0	1	0	0	1	1	0	1
						1	1	0	1	0	1	1	0	0	1
*							0	0	1	0	1	0	0	1	1
*								0	0	1	0	1	0	0	1
									1	1	0	1	0	1	1
										1	1	0	1	0	1
*											0	0	1	0	1
												1	1	0	1
*													0	0	1
														1	1
															1
	1	2	-1	-2	-1	0	3	-4	-1	0	1	0	-3	-2	15

Теперь построим функции корреляции для информационного сигнала с мешающим воздействием

Вход	0	1	0	1	1	1	1	0	0	0	1	0	0	1	1
	0	1	0	1	1	1	1	0	0	0	1	0	0	1	1
		1	0	1	1	1	1	0	0	0	1	0	0	1	1
*			1	0	1	0	0	0	0	1	1	1	0	1	1
*				1	0	1	0	0	0	0	1	1	1	0	1
*					1	0	1	0	0	0	0	1	1	1	0
						0	1	0	1	1	1	1	0	0	0
*							1	0	1	0	0	0	0	1	1
*								1	0	1	0	0	0	0	1
									0	1	0	1	1	1	1
										0	1	0	1	1	1
*											1	0	1	0	0
												0	1	0	1
*													1	0	1
														0	1
															0
	-1	0	1	0	3	0	3	-4	-5	-2	1	0	1	-2	7

Построим функции корреляции для синхросигнала с мешающим воздействием

Вход	1	1	0	1	0	1	1	0	0	1	0	0	0	1	1
	1	1	0	1	0	1	1	0	0	1	0	0	0	1	1
		1	1	0	1	0	1	1	0	0	1	0	0	0	1
*			0	0	1	0	1	0	0	1	1	0	1	1	1
*				0	0	1	0	1	0	0	1	1	0	1	1
					1	1	0	1	0	1	1	0	0	1	0
*						0	0	1	0	1	0	0	1	1	0
*							0	0	1	0	1	0	0	1	1
*								0	0	1	0	1	0	0	1
									1	1	0	1	0	1	1
										1	1	0	1	0	1
											1	1	0	1	0
												1	1	0	1
*													0	0	1
														1	1
*															0
	1	2	-1	-2	1	0	-1	0	-5	4	3	-2	-5	4	7

Сведем результаты расчетов в таблицу:

Обозначение	Расчет
Эффективные значения относительных среднеквадратичных ошибок этапов входных преобразований и ошибки, вызванной действием помех
Значение частоты дискретизации Fд	3,6кГц
Значение пикфактора H	4
Число разрядов двоичного кода, Nр	10
Ширина спектра сигнала ИКМ-ОФМ , кГц	43
Требуемое значение отношения сигнал/шум для обеспечения пропускной способности канала связи	241220,67
Требуемое отношение q2 при оптимальном когерентном приеме	24
Требуемое отношение q2 при оптимальном некогерентном приеме	27,3