5. Расчетные характеристики материалов и расчет элементов на растяжение, смятие, скалывание, поперечный изгиб, косой изгиб, расчет сжато-изогнутых и растянуто-изогнутых элементов.

Э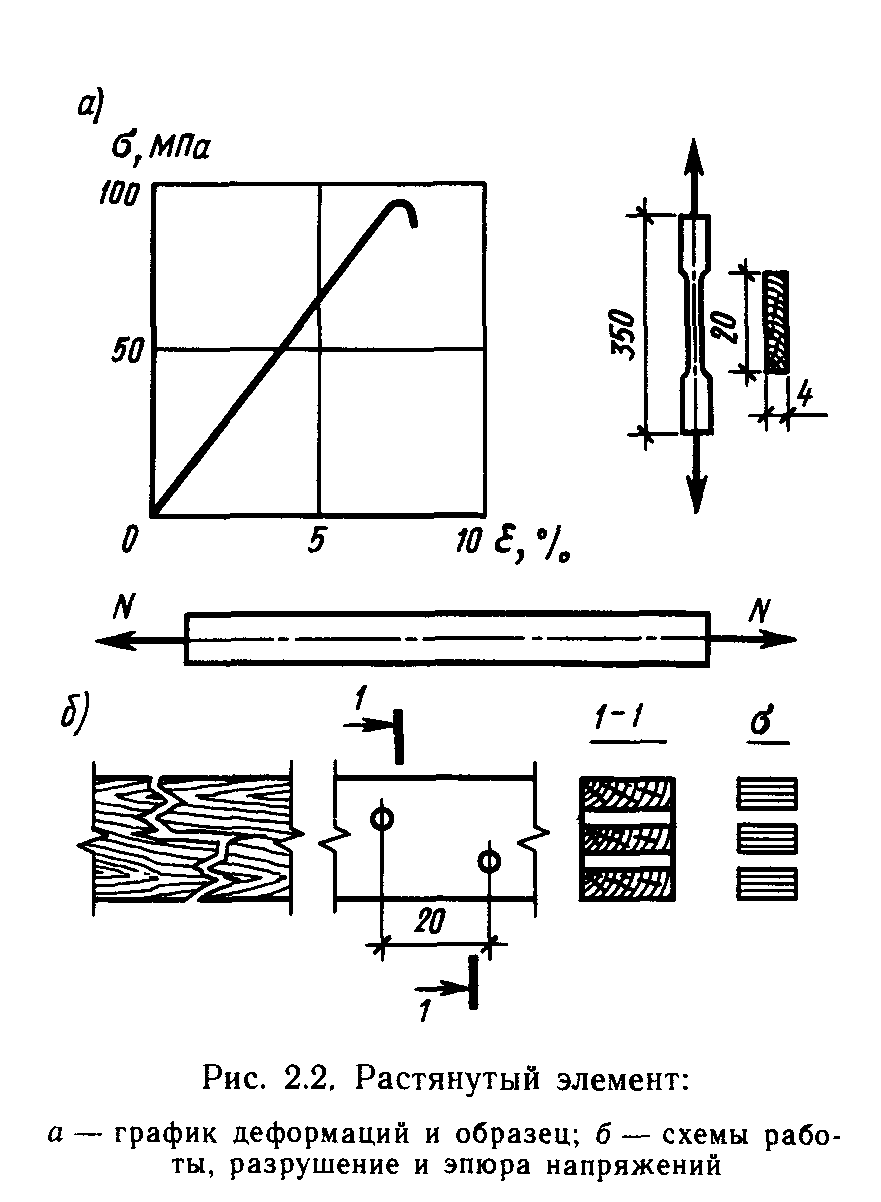 лементами деревянных конструкций служат доски, брусья, бруски, бревна цельных сечений с размерами, указанными в сортаментах пиленых и круглых лесоматериалов. Усилия, действующие в элементах конструкций, и их прогибы определяются общими методами строительной механики. В результате их расчета решаются ряд практических задач роектирования деревянных конструкций. Проверка прочности и прогиба элемента заключается в определении напряжений в сечениях, которые не должны превышать расчетных сопротивлений древесины, а также его прогибов, которые не должны превосходить предельных, допускаемых нормами. Подбор сечений при проектировании новых деревянных конструкций заключается в определении таких размеров элемента, при которых его прочность и устойчивость будут достаточны для воспринятия действующих усилий, а прогибы будут не более предельных. Несущая способность элемента определяется чаще всего в процессе обследования конструкций во время их эксплуатации. Для этого определяют наибольшие нагрузки и усилия, которые может выдерживать элемент известных размеров, чтобыпри этом расчетные сопротивления древесины и предельные прогибы не были превышены. Деревянные элементы рассчитывают на растяжение, сжатие, изгиб, растяжение или сжатие с изгибом, смятие и скалывание в соответствии с нормами СНиП П-25—80 «Нормы проектирования. Деревянные конструкции». Приводимые ниже расчетные сопротивления соответствуют древесине сосны и ели. В соответствии с этими же нормами производится расчет деревянных изгибаемых элементов по прогибам. Растянутые элементы — это нижние пояса ферм, затяжки арок и некоторые стержни других сквозных конструкций. Древесина работает на растяжение почти как упругий мате­риал и имеет высокую прочность. Разрушение растянутых эле­ментов происходит хрупко, в виде почти мгновенного разрыва.

Расчет по прочности растянутых элементов производится на растягивающую силу N от расчетных нагрузок:

Прочность растянутых элементов в тех местах, где они ослаб­лены отверстиями или врезками, снижается дополнительно в результате концентрации напряжений у их краев. Это учитывает­ся снижающим коэффициентом условий работы mр = 0,8.

С жатые элементы. На сжатие работают стойки, под­косы, верхние пояса и отдельные стержни ферм и других сквоз­ных конструкций.

Прочность стержня при сжатии и потеря устойчивости зависят от площади А и формы его сечения, длины l и типа закрепления его концов, что учитывается коэффициентом устойчивости φ, называемым иногда коэффициентом продольного изгиба. Сжатые деревянные элементы рассчитываются по прочности и устойчивости при действии продольных сил сжатия N от расчетных нагрузок:

Коэффициент устойчивости элемента ф определяется в зави­симости от его расчетной длины l₀, радиуса инерции сечения i, гибкости λ = l₀/i и находится из выражений φ = 3000/ λ² при λ >70 и φ = 1-0.8(λ/100)² при λ<=70.

Изгибаемые элементы — балки, доски настилов и обшивок — наиболее распространенные элементы деревянных конструкций.

Расчет изгибаемых элементов по прочности поперечных сечений производится на действие максимальных изгибающих момен­тов М (МН-м) от расчетных нагрузок :

где W — момент сопротивления сечения. У наиболее распростра­ненных прямоугольных сечений с шириной b и высотой h W = bh²/6, а для круглых сечений диаметром d W=d³/10.

Расчет изгибаемого элемента по прогибам заключается в оп­ределении его наибольшего относительного прогиба f/l от норма­тивных нагрузок и проверке условия, чтобы он не превосходил предельно допускаемого нормами значения, что определяется условием f/l≤[f/l].

Проверить относительный прогиб однопролетной шарнирно опертой балки прямоугольного сечения bxh, пролетом l при равномерной нормативной нагрузке q_н (МН/м) можно по формуле

С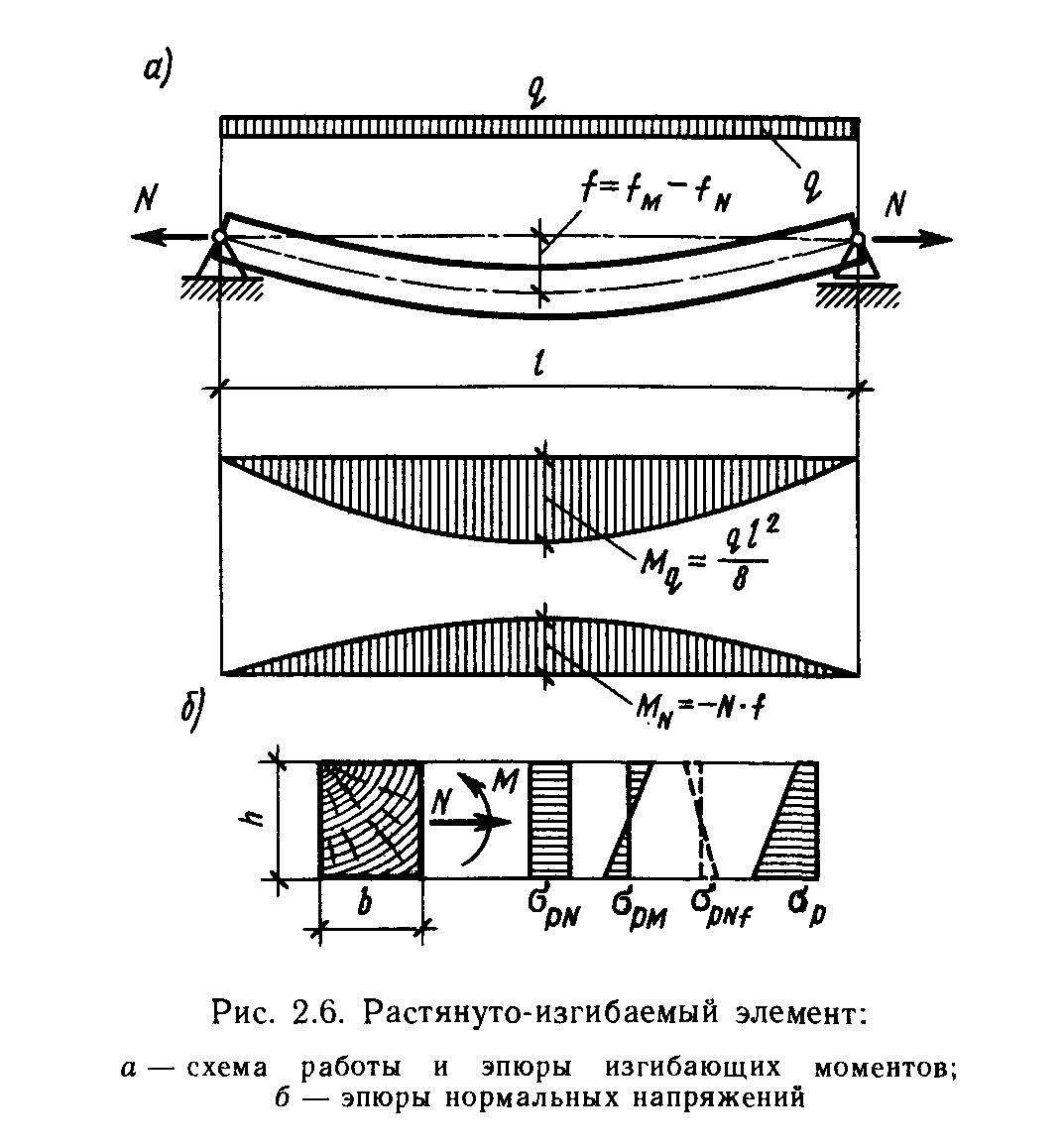 жато-изгибаемые элементы работают одновремен-но на сжатие и изгиб. Так работают, например, верхние пояса ферм, в которых кроме сжатия действует еще изгиб от междуузловой нагрузки от веса покрытия. В элементах, где сжимающие силы действуют с эксцентриситетом относительно их осей, тоже возникает сжатие с изгибом. Поэтому они называются также внецентренно сжатыми.

Расчет сжато-изгибаемого элемента производится на действие максимальных продольных сжимающих сил N и изгибающих моментов М от расчетных нагрузок по формуле

где М_Д=М/ξ, а коэффициент ξ=1-Nλ²/(3000R_cA); М_Д — это из­гибающий момент с учетом дополнительного изгибающего мо­мента, который возникает в результате прогиба элемента f от внешней нагрузки. При этом сжимающие продольные силы N начинают действовать с эксцентриситетом, равным /, и возни­кает дополнительный момент М = Nf Этот доп. мо­мент и учитывается коэффициентом ξ, который зависит от про­дольной силы N. гибкости λ расчетного сопротивления сжатию R_c и площади сечения А.

С жато-изгибаемый элемент должен быть также проверен на прочность и устойчивость только при сжатии продольной силой в направлении из плоскости действия изгибающего момента:

Расчет сжато-изгибаемых элементов.

Метод расчета сжато-изгибаемых элементов состав­ного сечения на податливых связях остается таким же, как и элементов цельного сечения, но в формулах допол­нительно учитывается податливость связей.

При расчете в плоскости изгиба составной элемент испытывает сложное сопротивление и податливость свя­зей учитывают дважды:

1. Введением коэффициента кю, такого же как при расчете составных элементов на поперечный изгиб;

2. 2. вычислением коэффициента ξ с учетом приведенной гибкости элемента.

3. Нормальные напряжения определяют по формуле

4. 

5. г де М_Д = М/ξ, а коэф. Ξ = 1-Nλп²/(3000R_cA); λп = μ λц

6. При определении количества связей, которое надо поставить на участке от опоры до сечения с максималь­ным моментом, учитывают возрастание поперечной силы при сжато-изгибаемом элементе:

7. 

8. В стержнях с короткими прокладками помимо обще­го расчета стержня необходима еще проверка наиболее напряженных ветвей как сжато-изгибаемых стержней по формуле:

9. 

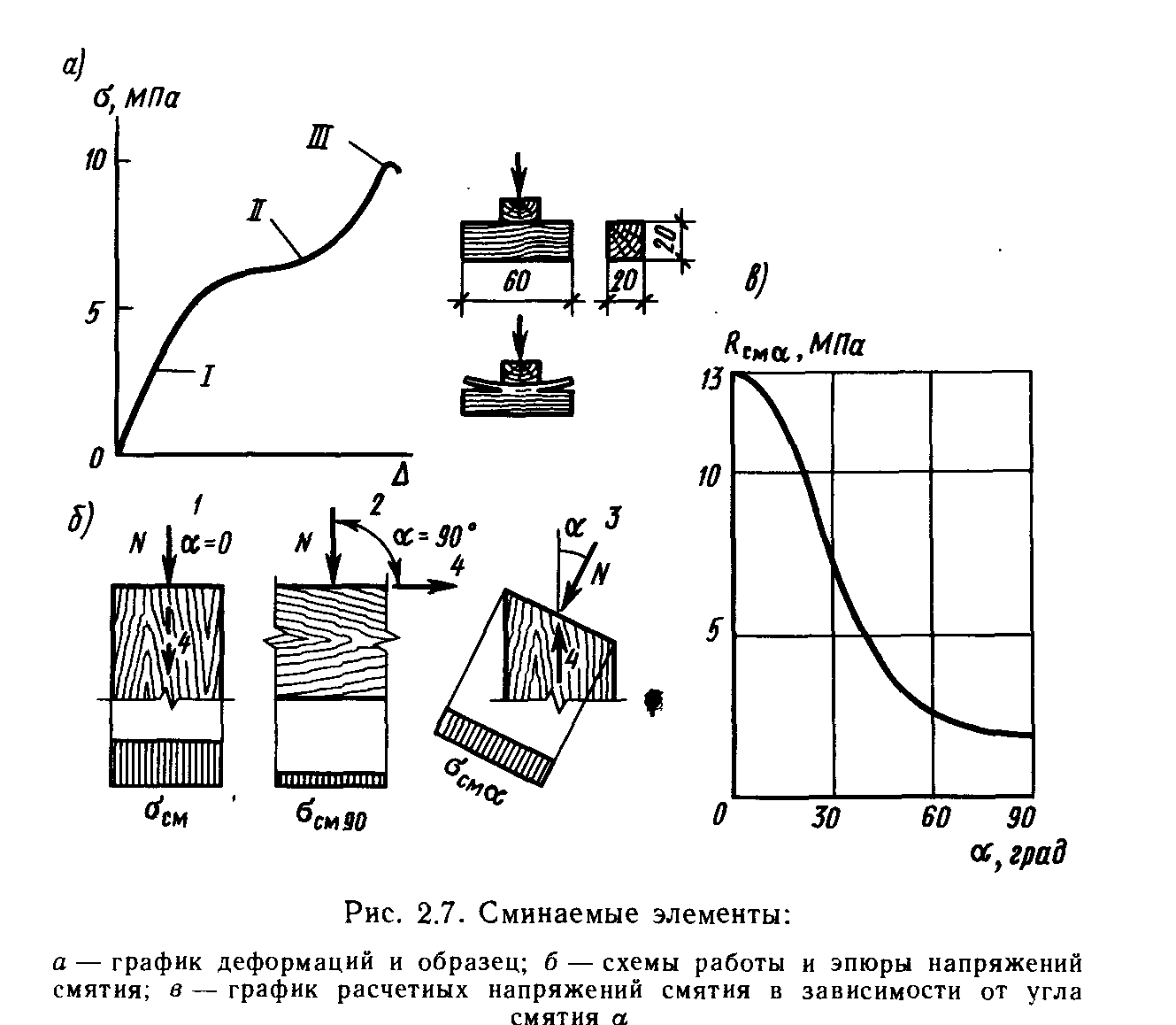
Смятие древесины — это поверхностное сжатие, которое может быть общим и местным.

Прочность и деформативность элементов при смятии сущест­венно зависят от угла смятия. Угол смятия а — это угол между направлениями действия сминающей силы и волокон древесины.

Расчет элементов на смятие производится на действие сжи­мающей силы N от расчетных нагрузок, площади смятия А и расчетного сопротивления древесины Rсма по формуле:

Скалывание древесины. Расчет изгибаемых элементов на скалывание при изгибе производится на действие максимальных поперечных сил Q (МН) от расчетных нагрузок по формуле

Податливостью называется способность связей при деформации конструкций давать возможность соединяе­мым брусьям или доскам сдвинуться один относительно другого.

Податливость связей ухудшает работу составного элемента по сравнению с таким же элементом цельного сечения. У составного элемента на податливых связях уменьшается несущая способность, увеличивается деформативность, изменяется характер распределения сдвигающих усилий по его длине, поэтому при расчете и проектировании составных элементов необходимо учи­тывать податливость связей.

Вопросы учета податливости связей при расчете со­ставных стержней были впервые разработаны в СССР.

Расчет на поперечный изгиб.

Геометрические ха­рактеристики составной балки на податливых связях Jп, Wп можно выразить через геометрические характе­ристики балки цельного сечения, умноженные на коэф­фициенты меньше единицы, которые учитывают подат­ливость связей:

Jп = Кж ∙ Jц, где Кж = 1… Jо / Jц

Wп = Кж ∙ Wц, где Кж = 1… Wо / Wц

Расчет составной балки на податливых связях сво­дится, таким образом, к расчету балки цельного сече­ния с введением коэффициентов, учитывающих подат­ливость связей. Нормальные напряжения определяют по формуле:

Прогиб составной балки на податливых связях опре­деляют в общем случае по формуле:

Значения коэффициентов Кw и Кж приводятся в СНиП 11-25-80 «Деревянные конструкции. Нормы проектиро­вания».

Количество связей определяют расчетом на сдвига­ющие усилия. Сдвигающее усилие Т по всей ширине балки, равное τ∙b, вычисляют по формуле Т = QS / J.

При расчете количества связей должны быть со­блюдены два условия:

1) число равномерно поставленных связей на участке балки от опоры до сечения с максимальным моментом должно воспринять полное сдвигающее усилие

2) связи, поставленные около опор, не должны быть перегружены.

Расчет на продольный изгиб.

Расчет составных элементов на податливых связях при продольном изгибе как и при поперечном изгибе мо­жет быть сведен к расчету элементов цельного сечения с введением коэффициента, учитывающего податливость связей. Возможные сдвиги в швах при продольном из­гибе значительно меньше, чем при поперечном изгибе. При расчете на продольный изгиб напряжения вычис­ляют по формуле:

Усилие N и расчетную площадь элемента Fрасч опре­деляют как и в элементах цельного сечения, а приведен­ную гибкость (от которой зависит коэффициент продоль­ного изгиба ф) находят по формуле: λп = μ ∙ λц.

В составном элементе с одинаковым закреплением по концам целесообразно ставить четное количество связей. При их нечетном количестве одна связь будет поставле­на в середине элемента, где сдвига не происходит, и, сле­довательно, поставленная связь не будет работать. Это указание относится особенно к составным элементам с малым количеством связей.

Косоизгибаемые элементы — это балки и прогоны скатных покрытий. Косой изгиб возникает в элементах, оси сечений которых расположены наклонно к направлению действия нагрузок. При косом изгибе нормальные напряжения в сечениях суммируются и достигают максимальных значений только сжатия в верхней, а растяжения — в нижней точках сечений. В этих точках и начинается разрушение косоизгибаемого элемента прямоугольного сечения. В элементах

круглого сечения косой изгиб возникнуть не может, поскольку все его оси являются осями симметрии сечения. Вертикальная нагрузка, например, равномерная q, и изгибающий момент от нее М при косом изгибе элемента прямоугольного сечения под углом а раскладываются на нормальные и скатные составляющие вдоль осей сечений: qx = q cos a; qy=q sin а; Mx = M cos а; Му = М sin а. Относительно этих же осей определяются моменты сопротивления W и момент инерции / сечений. Проверка прочности косоизгибаемых элементов производится по

формуле a=Mx/Wx + My/Wy^R,. Расчет косоизгибаемых элементов по прогибам производится с учетом геометрической суммы прогибов относительно каждой оси по формуле f/l = /l<=[f/l] Подбор сечений косоизгибаемых элементов может производиться методом попыток. При этом их следует устанавливать большими размерами прямоугольного сечения в направлении действия больших составляющих действующих нагрузок.