11) Записать условие потенциальности электростатического поля в интегральной и дифференциальной форме.

Электрическое поле в диэлектриках.

1) Что такое вектор поляризации диэлектрика; диэлектрическая восприимчивость; диэлектрическая проницаемость?Для количественного описания поляризации диэлектрика вводится величина наз.вектором поляризации(P)Если диэлектрик поляризован однородно, поляризованность равна сумме дипольных моментов молекул, содержащихся в единице объема вещества Для количественного описания поляризации диэлектрика пользуются векторной величиной — поляризованностью, определяемой как дипольный момент единицы объема диэлектрика: Если диэлектрик изотропный и Е не слишком велико, то где { — диэлектрическая восприимчивость вещества, характеризующая свойства ди­электрика. Диэлектрическая проницаемость В ВАКУУМЕ=1.

2) В каком случае возникают объёмные связанные заряды; чему равна их объёмная плотность?

В результате процесса поляризации в объеме (или на поверхности) диэлектрика возникают нескомпенсированные заряды, которые называются поляризационными, или связанными. Частицы, обладающие этими зарядами, входят в состав молекул и под действием внешнего электрического поля смещаются из своих положений равновесия, не покидая молекулы, в состав которой они входят. Связанные заряды характеризуют поверхностной плотностью Если вектор поляризации P различен в разных точках объема диэлектрика, то в диэлектрике возникают объемные поляризационные заряды, объемная плотность которых .

3) Что такое вектор электрического смещения?Связанные заряды, как и любые другие электрические заряды. являются источниками электрического поля. поэтому при вычислении поля в диэлектриках, наряду с плотностью р сторонних зарядов, нужно учитывать плотность р связанных зарядов. Следовательно, при наличии диэлектриков должна быть написана в виде divE=1/e0(p+p) Введем вспомогательную величину, источниками которой является только сторонние силы.divE=1/e0(p-divP) запишем так div(e0E+P)=p Следовательно D=e0E+P вспомогательная величина. Ее дивергенция определяется плотностью только сторонних зарядов называемой электрическим смещением пол.!

4) Сформулировать теорему Гаусса для вектора электрического смещения в интегральной и дифференциальной форме.

Понятие потока вектора является одним из важнейших понятий векторного анализа. Оно используется при формулировке важнейших свойств электрического, магнитного и других векторных полей. Первоначально это понятие было введено в гидродинамике. Возьмем в поле скоростей жидкости малую площадку S, перпендикулярную к вектору скорости жидкости v (рис. 12). Объем жидкости, протекающей через эту площадку за время dt, равен νS dt. Если площадка наклонена

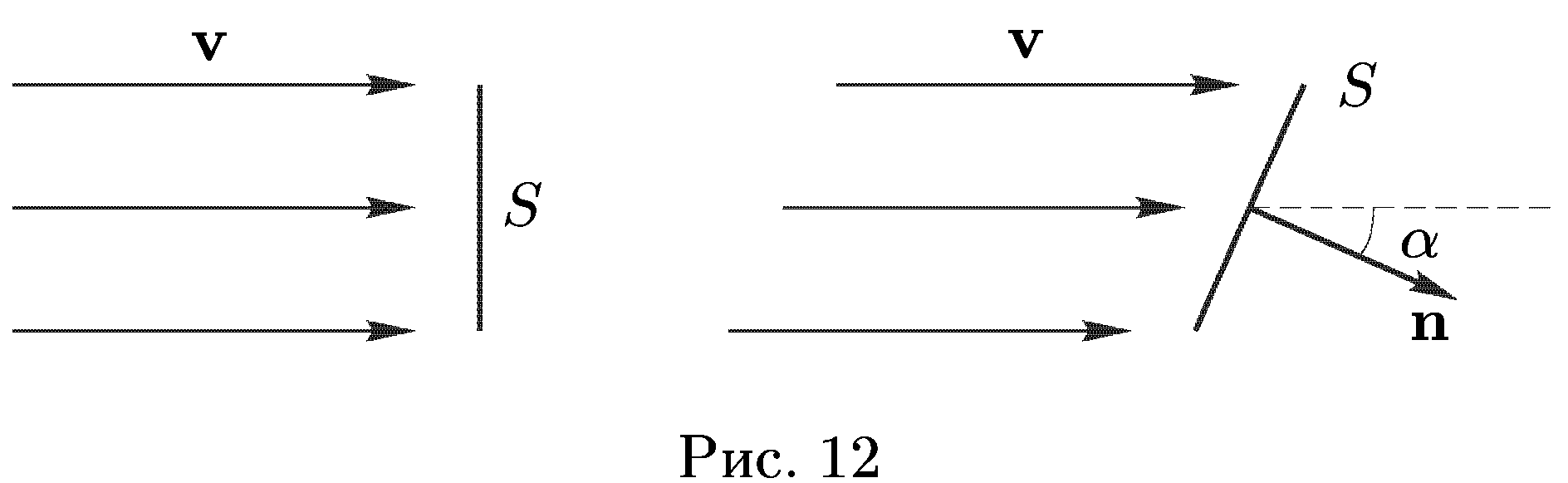к потоку, то соответствующий объем будет νS cosαdt, где α — угол между вектором скорости ν и нормалью n к площадке S. Объем жидкости, протекающей через площадку S в единицу времени, получится делением этого выражения на dt. Он равен νScosα, т.е. скалярному произведению (vS) вектора скорости v на вектор площадки S = Sn. Единичный вектор n нормали к площадке S можно провести в двух прямо противоположных направлениях. Одно из них условно принимается за положительное. В этом направлении и проводится нормаль n. Та сторона площадки, из которой исходит нормаль n, называется внешней, а та, в которую нормаль n входит, — внутренней. Если поверхность S не бесконечно мала, то при вычислении объема протекающей жидкости ее надо разбить на бесконечно малые площадки dS, а затем вычислить интеграл ∫(vdS) по всей поверхности S.

Выражения типа (v dS) или ∫(vdS) встречаются в самых разнообразных вопросах физики и математики. Эти выражения имеют смысл независимо от конкретной физической природы вектора v. Они называются потоком вектора v через бесконечно малую площадку dS или конечную поверхность S соответственно. Так, интеграл Ф = ∫ E dS называют потоком вектора напряженности электрического поля Е, хотя с этим понятием и не связано никакое реальное течение. Допустим, что вектор Е представляется геометрической суммой E = ∑E_i

Умножив это соотношение скалярно на dS и проинтегрировав, получим

где Ф₁,Ф₂ … — потоки векторов E₁, E₂ ... через ту же самую поверхность. Таким образом, из того факта, что векторы складываются геометрически, следует, что их потоки через одну и ту же поверхность складываются алгебраически.

Перейдем теперь к доказательству важнейшей теоремы электростатики — теоремы Гаусса. Она определяет поток вектора напряженности электрического поля через произвольную замкнутую поверхность S. За положительную нормаль к поверхности S примем внешнюю нормаль, т.е. нормаль, направленную наружу (рис. 13). Предположим

сначала, что электрическое поле создается единственным точечным

Рис. 13

сначала, что электрическое поле создается единственным точечным зарядом q. На поверхности S поле определяется выражением

(5.2)

Рассмотрим сначала простейший случай, когда поверхность S является сферой, а точечный заряд q помещен в ее центре. Поток вектора Е через элементарную площадку сферы равен

а поток через всю сферу Ф = qS/r². Так как поверхность сферы S равна 4πr², то

Покажем теперь, что результат не зависит от формы поверхности S, окружающей заряд q. Возьмем произвольную элементарную площадку dS с установленным на ней положительным направлением нормали n (рис. 14). Поток вектора Е через эту площадку будет

где dS_r — проекция площадки dS на плоскость, перпендикулярную к радиусу r. Используя выражение (5.2), получим dФ = qdS_r/r². Величина dS_r/r² есть телесный угол dΩ, под которым из точки нахождения заряда q видна площадка dS_r, а следовательно, и площадка dS. Условимся считать его положительным, если площадка dS обращена к q внутренней стороной, и отрицательным в противоположном случае.Тогда dФ = q dΩ. Поток Ф через произвольную (вообще говоря, незамкнутую) конечную поверхность S найдется интегрированием этого выражения по dΩ. Так как заряд q не зависит от положения площадки dS, то

где Ω — телесный угол, под которым из точки нахождения заряда q видна поверхность S.

Случай, когда точечный заряд q лежит точно на поверхности S, физического смысла не имеет. Точечный заряд есть идеализация, пользоваться которой допустимо только в тех случаях, когда линейные размеры заряженного тела малы по сравнению с расстояниями, на которых рассматривается поле этого тела. Если же заряд лежит на поверхности, то точки последней вблизи самого заряда этому условию не удовлетворяют. Допустим, что поле Е является суперпозицией полей E₁, E₂... точечных зарядов q₁, q₂… По теореме, доказанной выше, поток вектора Е равен сумме потоков векторов E₁, E₂,... Если заряд qi окружен замкнутой поверхностью S, то его поток через эту поверхность будет 4πq_i. Если же заряд лежит во внешнем пространстве по отношению к поверхности S, то его поток равен нулю. В результате получается следующее фундаментальное соотношение:

называемое электростатической теоремой Гаусса. Здесь q — алгебра- ическая сумма всех зарядов, окруженных замкнутой поверхностью S. Заряды, расположенные во внешнем пространстве по отношению к этой поверхности, на величину потока не влияют.

Соотношение (5.5) выражает теорему Гаусса в интегральной форме. Придадим теперь этой теореме дифференциальную форму. Назовем объемной плотностью электричества ρ количество электричества, отнесенное к единице объема. Тогда заряд в элементе объема dV представится выражением dq = ρ dV. Будем предполагать, что величина ρ является непрерывной функцией пространственных координат. Представление о непрерывном распределении электричества в пространстве является такой же идеализацией, как и представление о непрерывном распределении вещества. Такими представлениями широко пользуются в макроскопической физике. Возьмем в пространстве бесконечно малый прямоугольный параллелепипед со сторонами dx, dy, dz, параллельными координатным осям прямоугольной системы координат (рис. 25). На грани 1 рис 25 внешняя нормаль направлена в отрицательную сторону оси х. Поэтому поток вектора Е через эту грань будет —Е_x(х) dy dz. На противоположной грани 2, наоборот, направление внешней нормали совпадает с положительным направлением оси х, и для потока через эту грань следует писать +Ех(х + dx) dy dz. Сумма обоих потоков будет

где dV = dx dy dz — объем параллелепипеда. Аналогично найдутся потоки через две пары остальных граней. Полный поток через всю поверхность параллелепипеда:

Где введено обозначение

(7.2)

По теореме Гаусса тот же поток равен 4πq = 4πρ dV. Приравнивая оба выражения, получим

Эта формула и выражает электростатическую теорему Гаусса в дифференциальной форме.

Проводники в электрическом поле.

1) Что происходит при внесении проводника в электростатическое поле? Носители заряда в проводниках приходят в движение под действием сколь угодно малой силы. Поэтому для равновесия зарядов на проводнике необходимо выполнение двух условий:1-напряженность поля внутри проводника должна быть равна нулю E=0(потенциал внутри проводника должен быть постоянным 2-напряженность поля на поверхности проводника должна в каждой точке быть направлена по нормали к поверхности:E=En(в случае равновесия зарядов поверхность проводника является эквипотенциальной).