11. Формула Пуассона и условия ее применимости.

Использование формулы Бернулли при больших n и m вызывает трудности из-за громоздких вычислений => возникает необходимость в отыскании вероятности обеспечивающих необходимую точность.

Теорема: если число испытаний неограниченно увеличивается n и вероятность р наступления соб.А в каждом испытании уменьшается р , но так что их произведение n*p остается величиной постоянной (λ=np=const), то вероятность

Доказательство: λ=np => p=λ/n подставляем это равенство в формулу:

= = =

Перейдем к пределу в обеих частях неравенства при n :

,

=>

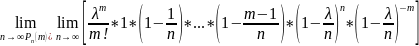
Формулу Пуассона применяют обычно когда n≥50, np≤10

12. Дискретные случайные события и возможности их описания.

Опр.: СВ- это переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений. (Примеры: число бракованных изделий в данной партии, расход электроэнергии предприятия)

Опр.: ДСВ – это СВ с конечным или бесконечным, но счетным множеством её значений (см.выше 1-ый пример)

Для случайных величин (далее - СВ) приходится использовать особые, статистические методы их описания.

Дискретное описание заключается в том, что указываются все возможные значения данной величины (например - 7 цветов обычного спектра) и для каждой из них указывается вероятность или частота наблюдений именного этого значения при бесконечно большом числе всех наблюдений.

Доказанно, что при увеличении числа наблюдений в определенных условиях за значениями некоторой дискретной величины частота повторений данного значения будет все больше приближаться к некоторому фиксированному значению - которое и есть вероятность этого значения.

13. Закон распределения дискретной случайной величины. Многоугольник распределения.

Опр.: Закон распределения СВ – это всякое соотношение устанавливающее связь между возможными значениями СВ и соответствующими ими вероятностями. Говорят, что СВ распределена по данному закону или подчинена этому закону распределения.

ЗАКОН распределения ДСВ может быть задан в виде таблицы:

х1	х2	…	хn
p1	p2	…	pn

Х:

- ряд распределения ДСВ

где, х_1, х_2,…, х_n – возможные значения СВ, в порядке возрастания

p₁, p₂,..., p_n – соответствующие им вероятности.

Очевидно, что суммы вероятностей p_i=1

Т.к.события Х=х, х=1,…,х= х_n образуют полную группу событий.

Закон распределения дискретной случайной величины может быть представлен в виде многоугольника распределения – фигуры, состоящей из точек, соединенных отрезками

Многоугольники унимодального (а), полимодального (б) и антимодального (в) распределений.