Министерство образования Российской Федерации

Московский инженерно-физический институт

(государственный университет)

В.В.Масленников

Сборник задач по курсу

"Основы электроники"

Москва 2003

УДК 621.38(076)

ББК 32.85я7

М31

Масленников В. В. Сборник задач по курсу "Основы электроники": Учебное пособие. - М.: МИФИ, 2003‑60 с.

В сборнике приведены задачи по расчету электронных схем и их решения. Рассматриваются вопросы расчета пассивных RC-цепей, простейших усилительных каскадов на транзисторах, аналоговых цепей, выполненных на интегральных операционных усилителях, логических элементов и импульсных устройств на их основе.

Все задачи сгруппированы по темам семинарских занятий курса "Основы электроники", читаемого студентам факультета «Т», причём часть из них обязательна для освоения материала, а часть предназначена для углублённого факультативного изучения курса.

Учебное пособие может быть также полезно всем, кто занимается изучением и проектированием аналоговых, импульсных и цифровых электронных схем.

Рекомендовано

редсоветом МИФИ

в качестве учебного пособия

ISB№5-7262-0278-3

(С) В.В. Масленников, 2003 г.

(С) Московский инженерно-физический институт

(государственный университет), 2003 г.

1. Пассивные rc – цепи Введение

В задачах рассматриваются вопросы расчета амплитудно-частотных, фазочастотных и переходных характеристик в пассивных RC- цепях.

Для расчета названных характеристик необходимо знать и уметь использовать законы Ома и Кирхгофа. Для расчета частотных характеристик пассивных RC- цепей необходимо помнить, что сопротивление конденсатора с ёмкостьюСсинусоидальному току определяется формулой:, где- круговая частота, j - мнимая единица. Для расчета переходной характеристики необходимо использовать закон коммутации: напряжение на емкости скачком измениться не может, а также учитывать, что сопротивление емкости в операторной форме имеет вид:.

Задача. 1.1Рассчитать и нарисовать амплитудно-частотную и фазочастотную характеристики интегрирующейRC- цепочки, приведенной на рис. 1.1. Сопротивление резистораR=10 кОм, емкость конденсатораC=1 нФ.

Рис. 1.1 Схема интегрирующейRC - цепочки

Решение.1. Определим передаточную функцию цепи:

.

Для этого воспользуемся вторым законом Кирхгофа: сумма ЭДС в замкнутом контуре равна сумме падений напряжений на участках цепи. Отсюда:

, ,

, (1.1)

где =RC- постоянная времениRC- цепи.

2. Из полученного выражения (1.1) можно получить формулы для расчета амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ) характеристик.

Для построения АЧХ необходимо найти модуль К(j). Из (1.1) получаем:

. (1.2)

Из условияопределяем значение верхней граничной частоты, при котором модуль коэффициента усиления уменьшается по сравнению с коэффициентом передачи при=0 враз:

и .

На рис. 1.2 приведен вид АЧХ интегрирующей RC - цепочки. При построении учитывалось, что .

Рис. 1.2. АЧХ интегрирующейRC - цепочки

Для построения ФЧХ умножим числитель и знаменатель передаточной функции (1.1) на комплексно - сопряженную величину

. (1.3)

Из (1.3) следует: ()=arctg(-)=-arctg(), т.е. напряжение на выходе цепи отстаёт от напряжения на входе.

Следует отметить, что на верхней граничной частоте сдвиг по фазе между выходным сигналом и сигналом генератора составляет 45.

На рис. 1.3 приведена фазочастотная характеристика интегрирующейRC - цепи.

Рис. 1.3 Фазочастотная характеристика интегрирующей RC ‑ цепи

Задача 1.2.Найти такие значения емкости и сопротивления интегрирующейRC- цепочки, при которых изменения сопротивления генератора и паразитной емкости нагрузки приводили бы к наименьшему изменению верхней граничной частоты. При этом f_В = 16 кГц, R_Г 100 Ом,С_П10 пФ.

Решение.1.СучетомR_ГиС_Псхему на рис. 1.1 можно заменить схемой на рис. 1.4 ,а и преобразовать к виду, изображенному на рис. 1.4,б, гдеR_ЭКВ=R_Г+R, аC_ЭКВ=С+С_П.

Рис. 1.4 Схема интегрирующей RC - цепочки с учетом сопротивления генератора и емкости нагрузки (а) и ее эквивалентное преобразование (б)

Схема на рис. 1.4,б аналогична схеме на рис. 1.1, поэтому

, _ЭКВ=R_ЭКВС_ЭКВ .

Полагая f_В=16 кГц, получаем

. (1.4)

Очевидно, что обеспечить необходимое значение _эквможно при разныхR_ЭКВиС_ЭКВ. Например, приR_ЭКВ=1 кОм и С_ЭКВ=10 нФ илиR_ЭКВ=100 кОм иС_ЭКВ= 100 пФ: _ЭКВ=10^-5с.

При R_ЭКВ=1 кОм изменениеR_Гможет привести к сравнительно большому изменению_ЭКВ, а приС_ЭКВ=100 пФ изменениеС_Пможет привести к большому изменению_ЭКВ.

2. Найдем оптимальное значение RиС. Для этого найдем производную.Выразим_ЭКВчерезRиС :

_ЭКВ=R(1+_R)C(1+_C)=(1+_R+_C+_R_C) , (1.5)

где ,,=RC.

Отсюда .

Пусть =const, тогда

=0.

Приравниваем производную нулю, получаем

.

Отсюда

RC_П=R_ГСили_R=_C=. (1.6)

3. Найдем RиСиз условия, что величины сопротивлений генератора и емкости нагрузки максимальны. Положим, что<<1. Отсюда _ЭКВRCи. Из (1.6) получаемФ²илиС=1 нФ, аR=10 кОм.

В этом случае максимальные значения _Rи_Cбудут равны 1%, а изменение верхней граничной частоты по сравнению со случаем, когдаR_Г=0 иС_П=0, составит 2%.

Задача 1.3.Рассчитать и нарисовать амплитудно-частотную и фазочастотную характеристики дифференцирующейRC- цепи, приведенной на рис. 1.5.

Р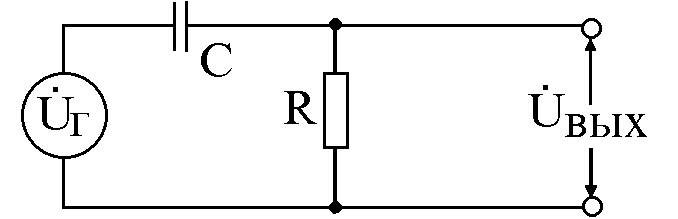ис. 1.5. Схема дифференцирующей RC – цепи

Решение.Задача решается аналогично задаче 1.1. Результаты решения приведены ниже. Передаточная функция цепи:

, где =RC;

, .

Амплитудно-частотная и фазочастотная характеристики цепи приведены на рис. 1.6,а и 1.6,б. При этом f_H - нижняя граничная частота цепи.

Рис. 1.6. Амплитудно-частотная (а) и фазочастотная (б) характеристики дифференцирующейRC - цепи

Задача 1.4.Рассчитать передаточную функцию дифференцирующейRC- цепи, учитывая влияние сопротивления генератораR_Ги паразитной емкости нагрузкиС_П. Нарисовать АЧХ схемы.

Решение.1. Передаточную функцию дифференцирующейRC- цепи с учетомR_ГиС_Гможно рассчитать из схемы, представленной на рис. 1.7.

Учитывая, что параллельное сопротивление резистора Rи емкостиС_П

равно , получаем:

(1.7)

Рис. 1.7. Схема дифференцирующейRC - цепи с учетом сопротивления генератора R_Г и паразитной емкости нагрузки С_П

2. Анализ (1.7) показывает, что имеет максимум при выполнении условия

₀²RCR_ГC_П=1. (1.8)

Отсюда

. (1.9)

При =₀ получаем

. (1.10)

Вид АЧХ представлен на рис. 1.8.

Рис. 1.8. АЧХ дифференцирующей цепочки с учетомR_Г и С_П

Задача 1.5.Определить верхнюю и нижнюю граничные частоты в схеме, приведенной на рис. 1.7, при условии, чтоR=100 кОм, С=0.1 мкФ,R_Г=50 Ом,С_П=50 пФ.

Решение. 1. Из (1.10) определим модуль коэффициента передачи цепи на частоте₀:

.

С учетом полученного результата представим передаточную функцию (1.7) в следующем виде:

. (1.11)

2. Из (1.11) можно сделать вывод, что передаточная функция цепи на низких частотах определяется передаточной функцией дифференцирующей RC- цепи с постоянной времениRС, а на высоких частотах - передаточной функцией интегрирующейRC- цепи с постоянной времениR_ГС_П.

Отсюда получаем: Гц, аМГц.

Задача 1.6.При замыкании ключа рассчитать переходной процесс в интегрирующейRC- цепи, схема которой приведена на рис. 1.9, и нарисовать график изменения выходного напряжения.

Рис. 1.9. Схема интегрирующей RC – цепи с источником постоянного напряжения и ключом

Решение.1. Заменяяjна операторрв формуле (1.1) получаем передаточную функцию цепи в операторной форме:

. (1.12)

Оригиналом данной передаточной функции является выражение

, где =RC . (1.13)

График зависимости K=f(t) приведен на рис 1.10.

Рис. 1.10. Переходная характеристика интегрирующей RC - цепи

2. Зная, что зависимость K(t) представляет собой экспоненту, можно построить переходную характеристику без нахождения передаточной функции. Для этого нужно определить напряжение на выходе интегрирующейRC- цепи приt=0 и приt=.

2.1. Полагая, что напряжение на конденсаторе не может измениться скачком, получаем:

U_С(0)=U_ВЫХ(0)=0, а, гдеI(0) ток в цепи приt=0.

2.2. При t=ток через резисторRпротекать не долженI()=0, следовательноU_ВЫХ()=U_С()=E-I()R=E.

Задача 1.7.Нарисовать график изменения выходного напряжения при замыкании ключа в цепочке дифференцирующего типа, приведенной на рис 1.11.

Решение.1. Полагая, что напряжение на емкости в первый момент должно равняться нулю, получаемE=I(0)(R_Г+R), U_ВЫХ(0)=I(0)R.

Отсюда .

Рис. 1.11. Схема RC - цепи дифференцирующего типа с источником постоянного напряжения и ключом.

2. При t=ток в цепи будет равен нулю, поэтомуU_ВЫХ()=I()R=0.

Постоянная времени заряда конденсатора равна =C(R_Г+R) .

Следовательно, график зависимости U_ВЫХ(t) будет иметь вид, представленный на рис 1.12.

Рис. 1.12. Переходная характеристика цепи, приведённой на рис.1.11.

Задача 1.8.Нарисовать импульс напряжения на выходеRC‑ цепи при подаче на вход схемы, приведенной на рис. 1.13, прямоугольного импульса с временем Т_И.

Рис. 1.13. Схема RC - цепи дифференцирующего типа с источником импульсного напряжения.

Решение.1. Прямоугольный импульс напряжения можно рассматривать как две ступеньки напряжения, смещенные во времени на времяТ_И.

Таким образом, задача сводится к нахождению реакции RC- цепи на каждую ступеньку напряжения (рис. 1.14).

Рис. 1.14. Представление прямоугольного импульса как суммы двух ступенек напряжения

2. Аналогично предыдущим задачам получаем:

U_ВЫХ1(0)=Е,,U_ВЫХ2(Т_И)=-Е,,, гдеU_ВЫХ1- выходное напряжение от воздействия первой ступеньки напряжения, аU_ВЫХ2‑ выходное напряжение от воздействия второй ступеньки.

3. Используя принцип суперпозиций, находим результирующее напряжение: U_ВЫХ(0)=Е,U_ВЫХ(Т_И)=-Е,U_ВЫХ()=0.

График выходного напряжения представлен на рис. 1.15.

Р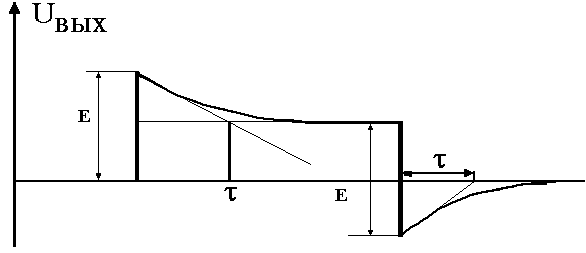ис. 1.15. График зависимостиU_ВЫХ=f(t) для RC - цепи дифференцирующего типа (рис. 1.13), при подаче на ее вход прямоугольного импульса

Задача 1.9. Нарисовать как измениться напряжение на выходе цепи, приведённой на рис.1.16, при замыкании ключа, если считать, что источник напряженияЕ– идеальный.

Рис.1.16. Цепь состоящая из двух конденсаторов с ключом и источником напряжения Е.

До замыкания ключа напряжение на выходе равно 0. После замыкания ключа в момент t₀, поскольку источникЕидеальный, произойдёт мгновенный заряд конденсаторовС₁иС₂. При этом нужно учесть, что заряды на конденсаторах будут равны:Q₁=Q₂=Q. Учитывая, чтоQ₁=C₁U₁,Q₂=C₂U₂, аE=U₁+U₂иU_ВЫХ=U₂, получаем. На рис.1.17 приведена зависимостьU_ВЫХ=f(t).

Рис. 1.17. Зависимость U_ВЫХ=f(t) для схемы на рис. 1.16.