Вопросы и задачи для самопроверки:

1. Сформулируйте закон коммутации для цепи, содержащей катушку индуктивности.

2. Нарисуйте интегрирующую и дифференцирующую RL-цепочки.

3. Может ли напряжение на индуктивности измениться мгновенно?

4. Может ли ток в цепи, содержащей индуктивность, измениться мгновенно?

5. Почему ток, протекающий по катушке индуктивности, не может измениться мгновенно?

6. Нарисуйте зависимостьU_ВЫХ после замыкания и размыкания ключей в следующих случаях (считать, что ключи в исходном состоянии были бесконечно долго):

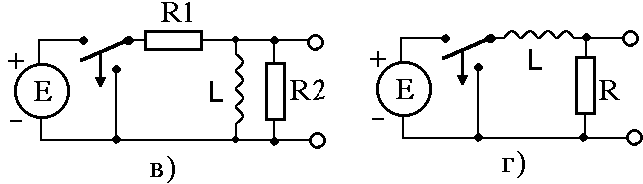
7. Какие процессы могут происходить в идеальном колебательном LC – контуре?

8. От каких параметров будет зависеть частота колебаний в LС-контуре?

9. Почему колебания в реальном LC – контуре будут затухающими?

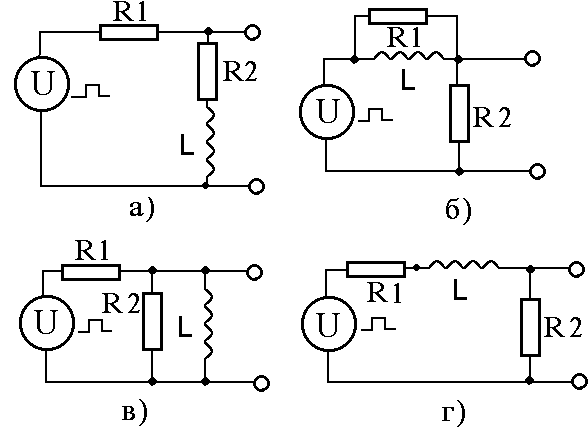10. Нарисуйте выходные импульсы напряжения, которые получатся при подаче на вход следующихRL-цепей прямоугольных импульсов:

1.5. RC-цепи при синусоидальном сигнале.

Рассмотрим характер процессов, происходящих в металлических проводниках при приложении к ним синусоидального источника э.д.с. Напомним, прежде всего, что при отсутствии э.д.с. электроны, находящиеся на внешней оболочке атомов и слабо связанные с ними, при комнатной температуре хаотически и с большими скоростями двигаются в различных направлениях, периодически сталкиваясь с ионизированными атомами. Усредненный по длительному интервалу времени суммарный вектор скоростей движения электронов равен 0. При приложении э.д.с. появляется суммарный вектор скоростей электронов, направленный от – к + источника э.д.с., т.е. возникнет дрейф электронов в одном направлении. При постоянной э.д.с. этот усредненный по времени вектор не изменяет амплитуду и направление.

При приложении к проводникам синусоидального э.д.с. усредненный вектор скоростей будет изменяться по синусоидальному закону. Если в рассматриваемом металлическом проводнике возникнет разрыв, то электроны не смогут двигаться в направлении действия э.д.с. и ток прекратится. Но если в место разрыва мы включим конденсатор, то ток в цепи не прекратится, т.к. конденсатор способен на одной пластине накапливать электроны, а затем освобождаться от них, отдавая их во внешнюю цепь.

Рассмотрим действие конденсатора, если к его клеммам подключен идеальный источник синусоидального тока (рис.1.46). Поскольку направление тока в источнике периодически изменяется на противоположное, конденсатор относительно общей шины будет заряжаться то до положительного напряжения, то до отрицательного. Очевидно, что при положительной полуволне синусоидального тока конденсатор от некоего отрицательного напряжения будет перезаряжаться до положительного. Рост положительного напряжения закончится, когда ток уменьшится до нуля. Этот момент будет соответствовать максимуму положительного напряжения, т.е. при синусоидальном токе напряжение будет отставать от тока на 90^о. После этого начнется период убывания напряжения.

Рис.1.46. Конденсатор, заряжаемый и разряжаемый источником синусоидального тока.

Нетрудно доказать высказанные соображения. Действительно поскольку , аполучаем

. (1)

Из полученного выражения можно сделать вывод: синусоидальный ток, протекающий через конденсатор, вызывает на нем синусоидальное напряжение, отстающее от тока на 90^о (рис.1.47).

Рис.1.47. Синусоидальные токи и напряжения на

конденсаторе.

Введем понятие сопротивления, обусловленного протеканием синусоидального тока по конденсатору Z_С. Из сути физических процессов, протекающих при перезарядке конденсатора при протекании по нему синусоидального тока, следует, что сопротивлениеZ_Cдолжно быть обратно пропорционально величине его емкости С. Действительно, чем меньше емкость конденсатора, тем меньше он способен аккумулировать заряд, тем меньший заряд он может отдать в цепь при изменении полярности напряжения, тем меньший ток потечет через него при приложенном синусоидальном напряжении, т.е. тем больше его сопротивление. С другой стороны, чем меньше частота, приложенного к конденсатору синусоидального тока, тем до большего напряжения он сможет перезарядиться, т.е. тем больше его сопротивление, что и следует из формулы (1).

В теории электрических цепей доказано, что

, (2)

где j– мнимая единица, показывающая, что синусоидальное напряжение на конденсаторе отстает от синусоидального тока, по нему протекающему, на 90^о,- круговая частота входного сигнала. Эта формула является ключевой при анализе цепей, содержащих источники э.д.с. и тока синусоидальной формы.

В случае, если входной генератор U_Г- источник синусоидального напряжения, для нахождения частотных характеристик цепи воспользуемся символическим методом. В этом методе учитывается не только величина амплитуды синусоидального сигнала (тока или напряжения), но и его фаза. С учетом фазы, например, синусоидальное напряжение можно записать следующим образом: Ũ=U₀sin(ωt+φ). Чтобы избавиться от такой сложной записи, вводят символическое обозначение U₀sin(ωt+φ)=. При этом закон Ома для сопротивленияRможно записать в следующей форме:. Поскольку сопротивление величина действительная ток и напряжение будут совпадать по фазе. Если вместо резистора поставить конденсатор, то закон Ома можно записать следующим образом:

, (3)

а поскольку Z_Свеличина мнимая напряжение будет отставать от тока на 90^о.

Заметим, что конденсатор можно считать линейным элементом, поскольку зависимость напряжения от тока при постоянной частоте синусоидального сигнала линейная характеристика, такая же как и для резистора.

Используя символический метод, можно также записать первый и второй законы Кирхгофа. Например, для интегрирующейRC– цепи (рис.1.48) по второму закону Кирхгофа сумма э.д.с. в замкнутом контуре в данном случаеравна сумме падений напряжений на резисторе и конденсаторе., где- комплексное сопротивление цепи.

Рис.1.48. Схема простейшей интегрирующей RC-цепи с синусоидальным источником э.д.с.

Используя этот закон, найдем комплексный коэффициент передачи цепи K(j)= /.

, ,

, (4)

где =RC - постоянная времени RC - цепи.

Из полученного выражения (4) можно получить формулы для расчета амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ) характеристик, часто используемых при описании цепей, находящихся под воздействием синусоидального сигнала.

Амплитудно-частотная характеристика какой-либо цепи это зависимость модуля коэффициента передачи цепи от частоты синусоидального сигнала. Фазочастотная характеристика это зависимость разности фаз между входным и выходным сигналами от частоты.

Умножим числитель и знаменатель передаточной функции (4) на комплексно - сопряженную величину. Получим

. (5)

Для нахождения АЧХ необходимо определить модуль (j). Из (5) получаем:

. (6)

Из условияопределяем значение верхней граничной частоты_В, при котором модуль коэффициента усиления уменьшается по сравнению с коэффициентом передачи при=0 враз:и. На рис.1.49а приведен вид АЧХ интегрирующей RC - цепочки. При построении учитывалось, что.

Например, если R=1 кОм, С=100 пФ, то=(10³*100*10^-12) с

=10^-7с=0,1мкс,f_ВГц ≈1,6МГц (1 мегагерц=10⁶Гц).

Для нахождения ФЧХ необходимо из (5) найти отношение мнимой и действительной части. При этом:

() = arctg(- )= - arctg(). Вид ФЧХ приведен на рис.1.49б.

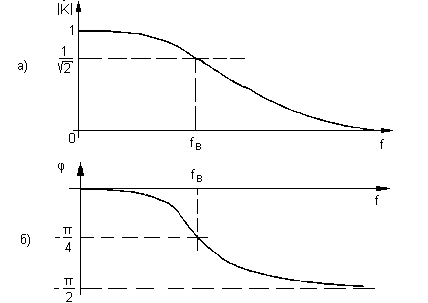
Рис.1.49. АЧХ (а) и ФЧХ (б) интегрирующей RC-цепи (рис.1.48).

Необходимо отметить, что на верхней граничной частоте сдвиг по фазе между сигналом генератора и выходным сигналом составляет ‑45, при=0=0, а при==‑/2.

Как уже подчеркивалось, дифференцирующая RC-цепь (рис.1.50) отличается от интегрирующей тем, что выходной сигнал снимается с резистора. Амплитудно-частотная и фазочастотная характеристики получаются из выражения для коэффициента передачи; который можно получить аналогично коэффициенту передачи для интегрирующей цепи

,

где τ=RC– постоянная времени дифференцирующей цепи.

Рис.1.50. Простейшая дифференцирующая RC-цепь с синусоидальным источником сигнала.

Тогда АЧХ (рис.1.51а) определяется из выражения , а ФЧХ (рис.1.51б):. При этом формула для нижней граничной частоты пропускания аналогична формуле для верхней граничной частоты интегрирующейRC-цепи: . На нижней граничной частоте сдвиг по фазе между сигналом генератора и выходным сигналом составляет +45^о, при =0 =/2, а при = =0. Например, если R=1 МОм (1 мегаом=10⁶ Ом), С=10 нФ, то =(10⁶*10*10^‑9) с=10^-2 с, а f_НГц≈16 Гц.

Рис.1.51. АЧХ (а) и ФЧХ (б) дифференцирующейRC-цепи (рис.1.50).

Опыт расчета простейших интегрирующих и дифференцирующихRC-цепей может быть использован и для расчета более сложных цепочек. Для примера рассчитаем интегрирующую RC-цепочку, схема которой приведена на рис.1.52а.

Рис.1.52. Схема интегрирующей RC-цепочки (а) и ее эквивалентная схема (б).

На рис.1.52б приведена эквивалентная схема цепи, в которой параллельное сопротивление резистора R₂ и конденсатора С заменено на эквивалентное комплексное сопротивление Z₂. Как было показано ранее сопротивление двух параллельно включенных резисторов R′ и R″ равно: . Отсюда для полученияZ₂ необходимо заменить R′ на R₂, а R″ на . В результате замены получим. Коэффициент передачи напряжения делителя, состоящего из двух сопротивленийR₁ и R₂, равен . ЗаменяяR₂ на Z₂, получим:

(7)

где τ=СR₁R₂/(R₁+R₂).

Сравнивая выражение коэффициента передачи для простейшей интегрирующей цепи (4) и полученное (7), заметим, что они отличаются лишь коэффициентом передачи на нулевой частоте и постоянной времени. АЧХ и ФЧХ цепи приведены на рис.1.53.

Рис.1.53. АЧХ и ФЧХ цепи, приведенной на рис.1.52.

Аналогично можно получить и комплексный коэффициент передачи интегрирующей RC-цепи, приведенной на рис.1.54, и часто используемой для коррекции АЧХ и ФЧХ электронных устройств.

Рис.1.54. Схема интегрирующей RC-цепочки с резистором, включенным последовательно с конденсатором.

В этом случае Z₂ определяется последовательным включением резистора R₂ и конденсатора С: .

Подставляя в коэффициент передачи резистивного делителя Z₂ вместо R₂, получаем

. (8)

АЧХ и ФЧХ такой интегрирующей RC-цепочки будут отличаться от АЧХ и ФЧХ простейшей интегрирующей RC-цепи. Для построения АЧХ найдем модуль . Чтобы упростить сейчас и при дальнейших расчетах процедуру нахождения модуля комплексного выражения, имеющего вид, убедимся, что. Действительно, умножая знаменатель и числитель выражения для на комплексно-сопряженную величину знаменателя, получаем:

Отсюда

ч.т.д.

Учитывая результаты приведенного доказательства,

получаем

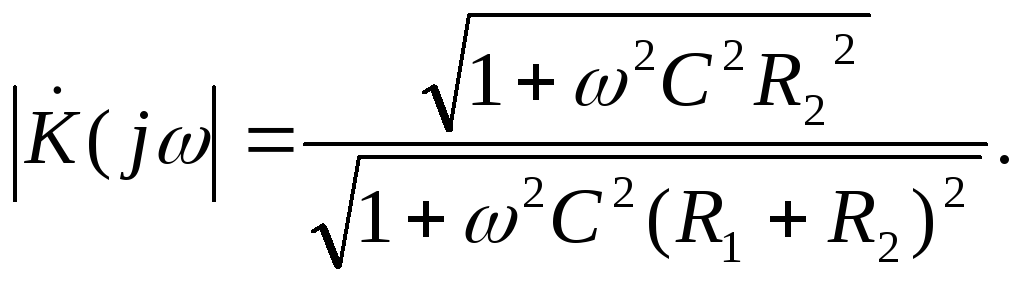
Полученное выражение позволяет достаточно просто построить АЧХ цепи. Для этого положим, что в первом случае ω→0, а во втором ω→∞. Отсюда: ,. Верхнюю граничную частоту схемы можно определить из условия. Отсюда. Анализ полученной формулы показывает, что приR₂=R₁(1+) знаменатель дроби равен 0, а, следовательно, верхняя граничная частота становится равной. При этом коэффициент передачи при = становится равным . ПриR₂>R₁(1+) верхняя граничная частота в схеме будет отсутствовать, т.к. коэффициент передачи будет всегда больше. АЧХ цепи для случаяR₁<R₂(1+) приведена на рис.1.55а.

Рис.1.55. АЧХ а) и ФЧХ б) схемы, приведенной на рис.1.54.

Графически изобразить вид АЧХ рассмотренной выше цепочки можно, и не прибегая к вычислению ││. Для этого нужно лишь учесть, что АЧХ любых RC-цепей, включающих в себя лишь один конденсатор, имеют монотонный характер. Следовательно, необходимо лишь определить ││при . Сделать это можно, если учесть, что реактивное сопротивление емкости равно .

При (это соответствует приложению ко входу постоянного напряжения) сопротивление емкости равно бесконечности. Ток в цепи протекать не будет, т.к. конденсатор заряжается до напряжения, равного входному . Так как =+I,а I = 0 , то = , т.е. ││=1.

При = ∞ сопротивление емкости равно нулю, а сопротивления образуют делитель напряжения. Отсюда ││= . По полученным значениям модуля коэффициента передачи при достаточно легко представить вид АЧХ рассматриваемой RC-цепи.

Для нахождения ФЧХ цепи домножим числитель и знаменатель выражения (8) на комплексно-сопряженную величину знаменателя. Получим:

.

Отсюда .

Заметим, что при ω→0, φ→0 и при ω→∞, φ→0. Нетрудно доказать, что φ имеет минимум при ,, (9)

причем при R₂=R₁: ₀_В, а при R₂<R₁: ₀>_В.

В зависимости от соотношения R₁ и R₂ минимум φ(ω₀) получается разной величины. Например, при R₁=R₂: φ(ω₀) 19^o, при R₁=2R₂: φ(ω₀)30^o, при R₁=3R₂: φ(ω₀)37^o, при R₁=8R₂: φ(ω₀)67^o. Примерный вид ФЧХ приведен на рис.1.55б.

Аналогично можно рассчитывать АЧХ и ФЧХ дифференцирующих цепей. Например, для схемы, приведенной на рис.1.56, получаем коэффициент передачи: , и модуль коэффициента передачи:.

Рис.1.56. Схема дифференцирующей RC-цепи с дополнительным резистором, включенным последовательно с

конденсатором.

Умножив числитель и знаменатель на множитель (R₁+R₂), получим:

. (10)

Заметим, что коэффициент передачи простейшей дифференцирующей цепи и схемы, приведенной на рис.1.56, отличаются лишь наличием множителя и величиной постоянной времени, которая в данном случае равна τ=С(R₁+R₂).

Д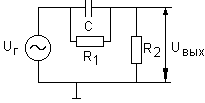ля схемы, приведенной на рис.1.57, получаем следующий коэффициент передачи:, где, τ₁=СR_{1 .}

Рис.1.57. Схема дифференцирующей RC-цепочки с

резистором, включенным параллельно с конденсатором.

Из формулы дляполучим, что модуль коэффициента передачи: . Для построения АЧХ учтем, что при ω=0, а при ω, K()=1. АЧХ цепи приведена на рис.1.58.

Рис.1.58. АЧХ схемы, приведенной на рис.1.57.

ФЧХ получается аналогично схеме, приведенной на рис.1.45, . Заметим, что при ω=0, φ=0, а при ω, φ=0. ФЧХ имеет максимум при .

. (11)

Нетрудно видеть, что выражения (9) и (11) отличаются лишь знаком. ФЧХ для R₁=3R₂ приведена на рис.1.59.

Р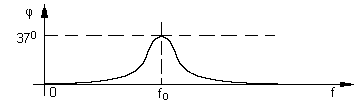ис.1.59. ФЧХ схемы, приведенной на рис.1.57,

при R₁=3R₂.

Используя приведенную методику, нетрудно вывести формулы коэффициентов передачи более сложных цепей, в том числе цепей с двумя конденсаторами.

Умение получать выражения для коэффициентов передачи RC-цепей в комплексной форме можно использовать для нахождения переходных характеристик. Для этого в выражении для сопротивления емкости синусоидальному току необходимо заменитьjω на оператор р. При этом получаем операторное выражение для сопротивления емкости . Законы Ома и Кирхгофа можно также выразить в операторной форме, заменяяİ на Ι(p) и на U(p). Используя эти замены, можно найти коэффициент передачи RC-цепи также в операторной форме. Сделаем это для простейшей интегрирующей RC-цепочки (рис.1.48). Запишем уравнения: ,. Отсюда, где τ=RC.

Для простейшей дифференцирующей RC-цепочки получим: , где τ=RC.

Для нахождения переходных характеристик теперь достаточно от операторной формы К(р) перейти к оригиналу К(t). Таблицы формул оригиналов и их операторных выражений для типовых случаев приводятся в учебниках [ ]. Таким образом, если возникают трудности в построении переходных характеристик RC-цепей, то можно используя операторный метод и таблицы перехода от операторной формы к оригиналам, получить выражения переходных характеристик RC-цепей.