Вопросы и задачи для самопроверки:

1. Что такое RC-цепь?

2. В каком случае конденсатор, включенный в цепь с источником постоянного напряжения, препятствует электрическому току, а в каком нет?

3. Сформулируйте закон коммутации для RC-цепи.

4. Обоснуйте справедливость закона коммутации.

5. Как определить изменение во времени напряжения на конденсаторе, если известен закон изменения во времени тока, заряжающего или разряжающего конденсатор?

6. Запишите закон изменения тока во времени для простейшей RC-цепи при замыкании ключа.

7. По какому закону происходит заряд конденсатора, осуществляемый от источника постоянного напряжения через резистор?

8. Может ли напряжение на конденсаторе измениться мгновенно? Почему?

9. Как рассчитываются переходные процессы в RC - цепях при воздействии прямоугольного импульса?

10. Как зарядятся два последовательно соединенных конденсатора, присоединенных к источнику постоянного напряжения?

11. Может ли какое-либо напряжение в цепи, содержащей конденсатор, изменится мгновенно?

12. Нарисуйтезависимость напряжения U_ВЫХ после замыкания и размыкания ключей в следующих схемах (считать, что ключи в исходном состоянии были бесконечно долго):

13. Нарисуйте выходные импульсы, которые получатся при подаче на вход следующих RC- цепочек прямоугольных импульсов.

1.4. Переходные процессы в rlc-цепях.

Для анализа переходных процессов, происходящих в цепях с катушками индуктивности, нужно знать соответствующий закон коммутации: ток в катушке индуктивности не может измениться скачком или мгновенно. Этот закон легко понять, если проанализировать формулу для магнитной энергии, накопленной в катушке индуктивности: . Предположим, что ток в катушке индуктивности изменился скачком. В этом случае должна мгновенно измениться магнитная энергия, т.е. источник электрической энергии, которая в катушке индуктивности преобразуется в магнитную энергию, должен обладать бесконечно большой мощностью, что невозможно: приΔt→0.

Используя этот закон, рассмотрим изменение напряжения на выходе вRL – цепи, приведенной на рис.1.41, после замыкания ключа (катушку индуктивности будем считать идеальной).

Рис.1.41. Интегрирующая RL – цепь.

По закону коммутации, сформулированному выше, ток в катушке не может измениться скачком. После замыкания ключа в момент t₀: I(t₀)=0. Следовательно, и ток через резистор в момент замыкания ключа будет равен нулю, т.е. U_ВЫХ(t₀)=I(t₀)R=0.

Таким образом, все напряжение Е в момент t₀ будет приложено к катушке индуктивности. Ток через катушку будет постепенно увеличиваться и при t= достигнет своего максимального значения, равного .

Нарастающий ток вызывает и нарастающее выходное напряжение. Нетрудно заметить аналогию между процессом в рассматриваемой схеме и переходным процессом в интегрирующей RC – цепи при подключении ее к источнику напряжения (см. рис.1.17). Как и для интегрирующей RC – цепи, напряжение на выходе будет изменяться по экспоненциальному закону, и цепь также можно считать интегрирующей (рис.1.42). Постоянная времени в этом случае будет равна =L/R. Например, если L=1 мГн (1 миллигенри =Гн), R=1 кОм, то =10^‑3/10³ с=10^-6 с=1 мкс.

Рис.1.42. Переходный процесс в интегрирующей RL – цепи.

В случае, если поменять местами R и L приведенная выше цепь превратится в дифференцирующую. Характер переходных процессов в этом случае будет аналогичен изменениям напряжения в дифференцирующей RC – цепи. Рассмотрим переходный процесс в колебательном контуре – цепи, состоящей из конденсатора и катушки индуктивности (рис.1.43).

Р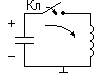ис.1.43. КолебательныйLC – контур с ключом.

Предположим, что конденсатор заряжен до некого напряжения U_C0, а катушка индуктивности и конденсатор идеальные. В этом случае при замыкании ключа (момент t₀) конденсатор начинает разряжаться через катушку индуктивности. Но в первый момент напряжение на конденсаторе не может измениться скачком, а ток через катушку индуктивности I_L сразу также не может измениться. Поэтому U_C(t₀)=U_C0, а I_L(t₀)=0. При t>t₀ напряжение на конденсаторе начнет уменьшаться, а ток возрастать (рис.1.44). В момент t₁ конденсатор полностью разрядится, т.е. электрическая энергия станет равной нулю, а ток возрастает до своего максимального значения. При этом в катушке в момент t₁ накопится максимальная магнитная энергия, которая не даст току мгновенно измениться до нуля. Ток будет продолжать протекать через катушку, а на пластинах конденсатора начнут накапливаться заряды, по знаку противоположные первоначальным. В момент t₂ ток уменьшится до нуля (магнитная энергия станет равной нулю), а конденсатор наоборот зарядится до напряжения, равного – U_C0. Дальше процесс будет происходить аналогично.

Рис.1.44. Незатухающие колебания в идеальном колебательном контуре.

Таким образом, в рассматриваемом идеальном LC – контуре возникнут незатухающие синусоидальные колебания (конденсатор и катушка индуктивности идеальны), обусловленные тем, что будут происходить процессы преобразования электрической энергии в магнитную, и наоборот. Вместе с тем, следует учесть, что в катушке происходит потеря энергии за счет протекания тока по проводам, имеющим сопротивление, т.е. часть энергии, запасенной в контуре, превращается в тепловую. Кроме того, происходит рассеивание электромагнитной энергии в пространство. Поскольку и в конденсаторе возникают токи утечки, то легко понять, что колебания в LC – контуре будут затухающие. На рис.1.45 приведена форма таких затухающих колебаний.

Рис.1.45. Затухающие колебания в реальном

колебательном LC–контуре.

Частота колебаний, как будет показано ниже, определяется формулой: . Напомним, что ω=2πf и, следовательно, f =-частота, измеряемая в Герцах – Гц. Например, еслиL=100 мкГн (1 микрогенри=10^-6 Гн), С=10 нФ, то f≈Гц≈160 кГц (1 килогерц=10³ Гц).