Вопросы и задачи для самопроверки:

1. Почему конденсаторы и катушки индуктивности называются реактивными элементами?

2. Какими свойствами обладает конденсатор?

3. Какими параметрами характеризуется конденсатор?

4. Чем определяются заряд и электрическая энергия, накапливаемая в конденсаторе?

5. Чем ограничены эти величины?

6. Чему будет равна электрическая энергия, накопленная в конденсаторе, подключенном к источнику постоянного напряжения?

7. За счет каких причин происходит разряд конденсатора?

8. Что из себя представляет катушка индуктивности?

9. Что происходит в катушке индуктивности при протекании по ней электрического тока?

10. Назовите основные виды катушек индуктивности.

11. Какими параметрами можно охарактеризовать катушку индуктивности?

12. От каких причин зависит значение индуктивности катушки?

13. Чем может быть ограничен максимальный ток, допускаемый для протекания через катушку индуктивности?

14. Что ограничивает магнитную энергию, накапливаемую в катушке индуктивности?

15. Что общего и различного в конденсаторе и катушке индуктивности?

1.3. Переходные процессы в rc-цепях.

В электрических цепях с реактивными элементами при воздействии на них изменяющихся во времени электрических сигналов следует учитывать, что накапливаемая и отдаваемая обратно в цепь энергия не может изменяться мгновенно. Это проявляется как при синусоидальном изменении во времени электрических сигналов (как, например, в электрической сети), так и при импульсных сигналах (как, например, в компьютерах). Рассмотрим сначала процессы в RC-цепях (цепях, составленных из резисторов и конденсаторов) при воздействии на них импульсных сигналов.

В зависимости от места включения конденсатора в цепь с постоянной э.д.с. он может либо полностью исключить прохождение электрического тока, либо, наоборот, совсем не оказывать влияния на его величину. Например, в цепи, приведенной на рис.1.14, постоянного тока не будет, т.к. через некоторое время после включения (в идеальном случае при t=) конденсатор зарядится до напряжения U_C=E. Поскольку э.д.с. источника и напряжение на конденсаторе компенсируют друг друга, ток через резистор отсутствует.По второму закону Кирхгофа: Е=U_C+U_R, где U_C и U_R падение напряжения на емкости и сопротивлении соответственно. Поскольку Е= U_C, то U_R=0. В свою очередь, т.к. U_R=IR, то I=0. Заметим, что если измерить напряжение на выходе цепи, то U_ВЫХ=U_R=0.

Рис.1.14. СхемаRC-цепи, в которой

конденсатор препятствует прохождению постоянного

электрического тока.

Всхеме резистивного делителя, приведенной на рис.1.15, постоянный ток (приt=) будет протекать, причем конденсатор не будет оказывать какое-либо влияние на его величину.

Рис.1.15. Схема резистивного делителя с конденсатором,

который не препятствует прохождению постоянного тока.

Действительно, как было показано выше, I=E/(R₁+R₂). Напряжение на конденсаторе равно напряжению на резисторе R₂ и, следовательно, U_С=IR₂=ER₂/(R₁+R₂). Когда конденсатор будет заряжен до напряжения U_C, он оказывать влияние на ток в цепи не будет. При этом U_ВЫХ=U_С.

Ситуация, описанная для схемы резистивного делителя с параллельно включенным конденсатором (рис.1.15), изменится, если конденсатор будет включен последовательно резистору R₂ (рис.1.16). В этом случае при t= конденсатор зарядится до напряжения U_С=Е, при этом ток будет равен 0: E=IR₁+U_С+IR₂, E=U_С, I(R₁+R₂)=0, I=0. Однако в отличие от схемы, приведенной на рис.1.14, напряжение на выходе не будет равным нулю. Действительно U_ВЫХ=U_С+IR₂ и т.к. I=0, а U_С=E получаем U_ВЫХ=Е.

Рис.1.16. Схема резистивного делителя с конденсатором, препятствующим прохождению постоянного тока.

Врассмотренных нами примерах полагалось, что электрические цепи работают в установившемся стационарном режиме (t=). Теперь положим, что электрическая цепь собрана с электрическим ключом (рис.1.17). Пример такого ключа – телеграфный ключ. В момент замыкания ключа в схеме возникнет переходной процесс, связанный с зарядом конденсатора.

Рис.1.17. Схема RC-цепи с ключом и источником э.д.с.

Рассмотрим этот переходный процесс. Замыкание ключа аналогично подаче на схему в момент t₀ сигнала, имеющего форму скачка напряжения (рис.1.18).

Рис.1.18. Скачок напряжения.

Сущность происходящего в цепи после замыкания ключа отражает один из законов коммутации, который гласит: напряжение на конденсаторе не может измениться скачком, т.е. мгновенно. Понять этот закон нетрудно, вспомнив, что электрическая энергия, запасенная в конденсаторе W, равняется:

, где С – емкость конденсатора,U_С– напряжение на его выводах. Если бы напряжение на конденсаторе могло бы измениться мгновенно, то, как следует из приведенной формулы, скачком бы изменилась и электрическая энергия, т.е. источник энергии, от которого конденсатор бы заряжался мгновенно, должен был бы иметь бесконечно большую мощностьP: приΔt→0. (Напомним, что мощность измеряется в Ваттах – Вт, причем 1 Вт=1 Дж/с.) Поскольку подобных источников электрической энергии в природе не существует, напряжение на конденсаторе будет изменяться постепенно.

Приведенные соображения позволяют понять, какие процессы будут протекать в приведенной на рис. 1.17 RC-цепи. В первый момент после замыкания ключа напряжение на конденсаторе по закону коммутации останется равным нулю. При этом поскольку по второму закону Кирхгофа Е=U_C(0)+I(0)R, аU_C=0, то ток в цепи в начальный момент времениI(0) будет равен:I(0)=E/R. Этим током конденсатор в первый момент и будет заряжаться. Но по мере зарядки конденсатора на нем будет создаваться падение напряжения, противодействующее напряжению источника э.д.с.

Для того чтобы найти закон изменения напряжения в цепи и закон изменения напряжения на конденсаторе нужно вспомнить, что сила тока определяется как количество заряда, проходящего через сечение проводника в единицу времени: .

Отсюда заряд в конденсаторе можно определить по формуле:,гдеI(t) – ток зарядки конденсатора,t₀– момент замыкания ключа,t_И– момент измерения.

Поскольку U_С=Q/C, получаем.

Второй закон Кирхгофа в рассматриваемой RC-цепи для любого момента времениt_Ибудет иметь следующий вид:. Решение этого уравнения дает следующий результат:, где τ=RC– постоянная времени заряда конденсатора. Например, еслиR=1 кОм, С=1 нФ, С= 1 нФ (1 нанофарада=10^-9Ф), то τ=(10³*10^-9) с=10^-6с=1 мкс (1 микросекунда равна 10^-6секунды).

График изменения тока от времени приведен на рис.1.19 (кривая а).

Рис.1.19. Зависимость тока вRC-цепи и напряжения на

конденсаторе от времени.

Изменения напряжения на конденсаторе U_C(t) будет происходить по закону: . График изменения напряжения на конденсаторе приведен на рис.1.19 (кривая б). ЗависимостиU=f(t) и I=F(t) называются переходными характеристиками цепи.

Предположим, что в схеме на рис.1.17 после достаточно долгого времени нахождение ключа в замкнутом состоянии, он размыкается. В этом случае, если считать конденсатор идеальным элементом напряжение на конденсаторе, равное Е, должно сохраняться бесконечно долго, т.к. цепь разряда конденсатора разомкнута. Однако конденсатор имеет хотя и большое, но конечное значение сопротивления утечки, шунтирующее, т.е. параллельно соединенное с емкостью конденсатора. Именно через это сопротивление напряжение на конденсаторе будет очень медленно разряжаться по экспоненциальному закону. Поскольку , по такому же закону будет изменяться напряжение на выходе цепи.

Рассмотрим наиболее типичные RC-цепи при воздействии на них импульсных сигналов.

Интегрирующие RC-цепи. Простейшая интегрирующая RC-цепь приведена на рис.1.20. Прямоугольный импульс (рис.1.21а), подаваемый на цепь от импульсного генератора U_Г, можно рассматривать как сумму двух скачков (двух ступенек) напряжения бесконечной длительности (рис.1.21б). Изменение напряжения на конденсаторе от действия одной ступеньки напряжения мы приводили выше. Две ступеньки напряжения дадут на выходе сигнал, форма которого приведена на рис.1.21в.

Рис.1.20.Схема интегрирующейRC-цепи.

Рис.1.21.а) прямоугольный импульс,

б) представление прямоугольного импульса в виде двух ступенек напряжения бесконечной длительности,

в) импульс на выходе интегрирующей RC-цепи (рис. 1.20).

Цепь называется интегрирующей, т.к. напряжение на выходе равно напряжению на конденсаторе, которое в свою очередь есть интеграл от тока зарядки. Ток зарядки конденсатора в первый момент равен U₀/R, т.е. в первый момент напряжение на выходе цепи, есть интеграл от входного напряжения. В последующие моменты времени ток будет уменьшаться, и зависимость нарушается. Поэтому можно считать, что интегрирующая RC-цепь интегрирует входное напряжение лишь в первый момент времени, т.е. при выполнении условия t_И<< можно считать, что .

Рассмотрим временные параметры интегрирующей RC-цепи, определяемые из переходной характеристики, при подаче на вход RC-цепи прямоугольного импульса напряжения (рис.1.22а). Поскольку напряжение на выходе цепи снимается с конденсатора, а по закону коммутации напряжение на конденсаторе не может измениться скачком, напряжение на выходе должно изменяться во времени постепенно. Анализ показывает, что оно будет изменяться по экспоненциальному закону и определяться по формуле: , гдеRC=τ – постоянная времени цепи.

Рис.1.22. Импульсы напряжения: а) на входе и б) на выходе интегрирующей RC-цепи.

Постоянную времени τможно определить как время, в течение которого выходное напряжение достигает значения, отличающегося от установившегося на 1/e. Графический способ определенияτ(из построенной переходной характеристики) показан на рис.1.22б.

Для характеристики переходного процесса обычно используют параметр t_Ф– время нарастания фронта, который определяется как время, в течение которого напряжение на выходе изменяется от уровня 0,1U_{ВЫХ.УСТ.}до 0,9U_{ВЫХ.УСТ.}(рис.1.22,б), гдеU_{ВЫХ.УСТ}– установившееся напряжение на выходеRC-цепи. Для рассматриваемойRC-цепиt_Фопределится формулой:t_Ф=2,2τ. Например, еслиR=10 кОм, С=10 пФ (1 пикофарада равна 10^-12Ф), тоτ=(2,2*0,1) мкс=0,22 мкс.

Иногда в электронных цепях используют более сложные интегрирующиеRC-цепи с дополнительными резисторами (рис.1.23).

Рис.1.23. Варианты интегрирующих RC-цепей.

Анализ показывает, что при подаче ступеньки напряжения на любую RC-цепь, содержащую один конденсатор, токи, протекающие через каждый компонент цепи, и напряжения в каждом из узлов будут изменяться по экспоненциальному закону. Для графического изображения необходимо лишь знать их значения при и t=∞ и вычислить постоянные времени.

Предположим, на вход цепи подается прямоугольный импульс с амплитудой и длительностью, много большей, чем время переходных процессов. Рассмотрим три варианта: а) R₁≠0, R₂=∞, б) R₁=0, R₂≠∞, в) R₁≠0, R₂≠∞.

Для случая а) схема будет иметь вид (рис.1.24).

Рис.1.24.Интегрирующая RC-цепь (вариант а)

схемы на рис.1.23.

Скачок напряжения вызовет ток в цепи, равный. Этот ток будет протекать по сопротивлениюR₁ и вызовет на нем падение напряжения U_R1, равное . Напряжение на выходе складывается из напряжения на конденсатореU_С и падения напряжения на сопротивлении R₁: U_ВЫХ=U_С+U_R1. Поскольку напряжение на конденсаторе в первый момент равно 0, напряжение на выходе будет равно , т.е. в первый момент на выходе возникнет скачок напряжения (рис.1.25). Затем будет происходить зарядка конденсатора по экспоненциальному закону с постоянной времени, равной τ₁=C(R+R₁) (по отношению к конденсатору резисторы R и R₁ включены последовательно, и их сопротивления складываются). Зарядка конденсатора будет происходить до тех пор, пока ток в цепи не прекратится. При t=∞ U_ВЫХ(∞)=U_С(∞), а U_С(∞)=U_Г, т.е. U_ВЫХ(∞)=U_Г. В момент окончания прямоугольного импульса также возникает скачок напряжения, равный , а затем экспоненциальное уменьшение напряжения до нуля.

Рис.1.25.Входной и выходной импульс для схемы на рис.1.24.

Д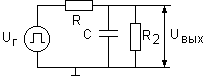ля случая б) схема интегрирующей цепи представлена на рис.1.26.

Рис.1.26.Интегрируюшая RC-цепь (вариант б)

схемы на рис.1.23.

Впервый момент скачка напряжения на выходе цепи не будет, т.к. выходное напряжение снимается с конденсатора, напряжение на котором скачком измениться не может (рис.1.27). В дальнейшем начнется заряд конденсатора. По мере увеличения на нем напряжения, часть тока, протекающего через резисторR, будет ответвляться в резистор R₂. В итоге на конденсаторе установится напряжение, равное . Заряд конденсатора будет происходить по экспоненциальному закону с постоянной времени, равной τ₂=CRR₂/(R+R₂), поскольку по отношению к конденсатору резисторы R и R₂ включены параллельно. При отрицательном скачке напряжения переходной процесс будет развиваться аналогично.

Рис.1.27.Входной и выходной импульс для RC-цепи,

приведенной на рис.1.26.

Для случая в) в первый момент возникнут токи в каждом из сопротивленийR, R₁ и R₂, что вызовет скачок напряжения на выходе. Эквивалентная схема для нахождения скачка напряжения в первый момент времени приведена на рис.1.28.

Рис.1.28.Эквивалентная схема для нахождения скачка напряжения в схеме на рис.1.23в.

Схема имеет такой вид, т.к. напряжение на конденсаторе в первый момент равно 0 и его можно считать закороченным. Из приведенной эквивалентной схемы следует, что (см. расчет схемы, приведенной на рис.1.10а).

Вдальнейшем напряжение на конденсаторе будет изменяться по экспоненциальному закону. Напряжение на выходе будет равноU_R2 и будет стремиться к уровню (рис.1.29), т.к. приt=∞ ток через конденсатор протекать не будет.

Рис.1.29.Входной и выходной импульс

для схемы на рис.1.23 (вариант в).

Постоянная времени изменения напряжения на выходе будет определяться постоянной времени изменения напряжения на конденсаторе, который будет заряжаться через резистор R₁ и параллельное сопротивление резисторов R и R₂: τ₁₂=C(R₁+RR₂/(R+R₂)).

ДифференцирующиеRC-цепи. Простейшая дифференцирующая RC-цепь образуется из интегрирующей заменой местами конденсатора на резистор (рис.1.30).

Рис.1.30. Простейшая дифференцирующая RC-цепь.

Напряжение на выходе цепи будет определяться падением напряжения на резистореR: U_ВЫХ(t)=U_R(t)=I(t)R. Зависимость I(t) для цепи, содержащей последовательное соединение резистора и конденсатора была нами приведена на рис.1.19. Следовательно, напряжение на выходе при условии, что постоянная времени много меньше времени импульса τ<<Т_И, будет иметь вид, представленный на рис.1.31 (окончание импульса входного напряжения означает отрицательный скачок напряжения).

Рис.1.31. Импульсы на входе и выходе дифференцирующей RC-цепи при условии  Т_И.

Цепь называется дифференцирующей, поскольку ток через конденсатор можно определить как производную от приложенного напряжения. Действительно, как было показано, , отсюда. Поскольку,. Как и в случае с интегрирующей цепочкой, можно считать, что дифференцирование входного напряжения происходит лишь в первый момент входного импульса.

Изменение напряжения на выходе дифференцирующей RC-цепочки также можно определить, зная изменение напряжения на выходе интегрирующей RC-цепи, т.к. и. Действительно, вычитая изU_Г(t) (рис.1.31а) напряжение U_C(t)=U_ВЫХ(t) (рис.1.19в), получаем U_ВЫХ(t)=U_R(t).

На рис.1.31 приведена эпюра выходного напряжения при подаче на дифференцирующуюRC – цепь прямоугольного импульса при условии, что постоянная заряда конденсатора много меньше длительности импульса  Т_И. Однако в электрических и электронных цепях возможно противоположное условие: >>Т_И. В этом случае напряжение на выходе будет иметь вид, представленный на рис.1.32.

Рис.1.32. Импульсы на входе и выходе дифференцирующей

RC – цепи при условии >>Т_И.

При этом искажение формы импульса можно охарактеризовать спадом плоской вершины импульса , величина которого определяется по формуле: =/U₁, где =U₁-U₂. Если постоянная времени  достаточно велика, то спад плоской вершины импульса происходит по линейному закону. В этом случае можно считать, что =Т_И/. Заметим, что возникающий отрицательный выброс  равен =U₁.

Например, если Т=100 мкс, U₁=1B, R=10 кОм, С=1 мкФ (1 микрофарада=10^-6 Ф), то =(10⁴*10^-6)=10^-2 с=10 мс (1 миллисекунда=10^-3 с), =100*10^-6/10^-2=0,01, а =(1*0,01) В=10 мВ.

Рассмотрим пример усложненной дифференцирующей RC-цепи с резистором, включенным параллельно конденсатору (рис.1.33).

Впервый момент подачи прямоугольного импульса напряжение на конденсаторе не может измениться. По этой причине все входное напряжение будет приложено к резисторуR₂, т.е. на выходе произойдет скачок напряжения, равный U_Г. При t=∞ и действии положительного скачка напряжение на резисторе R₂ будет уменьшаться и достигнет уровня . При этом зарядка конденсатора будет происходить с постоянной времени:. При воздействии отрицательного скачка напряжения переходной процесс будет происходить аналогично (рис.1.34).

Рис.1.33. Дифференцирующая RC-цепь с дополнительным резистором, включенным параллельно конденсатору.

Рис.1.34. Входной и выходной импульс дифференцирующейRC-цепи с дополнительным резистором, включенным

параллельно конденсатору.

Р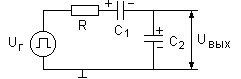ассмотрим теперьRC-цепи, включающие в себя два конденсатора и один резистор. Пример такой цепи приведен на рис.1.35.

Рис.1.35.RC-цепь с двумя конденсаторами и одним

резистором.

При подаче входного прямоугольного импульса в первый момент напряжения на конденсаторах будут равны 0, а все входное напряжение будет приложено к резистору R, что вызовет ток I(0)=U_Г/R.

Этим током конденсаторы будут заряжаться. При действии положительного скачка напряжения и t=∞ на конденсаторах установятся такие напряжения, которые создадут на правой пластине конденсатора С₁ такой отрицательный заряд, который будет равен положительному заряду на верхней пластине конденсатора С₂. Нейтрализоваться эти заряды не могут, т.к. приложено внешнее напряжение U_Г. Следовательно, Q_С1=Q_C2. Выразим заряды на конденсаторах через напряжения на них и значения их емкостей: C₁U_C1=C₂U_C2. Поскольку U_Г=U_C1+U_C2 (тока при t=∞ через конденсаторы не протекает, поэтому напряжение на резисторе равно 0), получаем: C₁(U_Г-U_C2)=C₂U_C2. Отсюда U_C2=С₁/(C₁+C₂)U_Г.

Постоянную времени заряда конденсаторов можно рассчитать, зная, чему равна емкость двух последовательно включенных конденсаторов. Эту емкость можно определить по тому заряду, который накопится в конденсаторе С₂ при приложении к двум последовательно соединенным конденсаторам напряжения U_Г : Q₂=C₂U_C2=C₁C₂/(C₁+C₂)U_Г=Q₁.Если приложить напряжение U_Г к некому конденсатору с емкостью С_ЭКВ - эквивалентной емкости двух последовательно включенных конденсаторов, то накопленный заряд будет равен: Q_ЭКВ=С_ЭКВU_Г0. Данный заряд Q_ЭКВ должен равняться зарядам на пластинах двух последовательно включенных конденсаторов. Приравнивая Q_ЭКВ=Q₂=Q₁, получаем: С_ЭКВU_Г=С₁С₂/(C₁+C₂)U_Г или С_ЭКВ=С₁С₂/(С₁+С₂) (отметим, что эквивалентное сопротивление двух последовательно включенных резисторов равно сумме их сопротивлений, а емкостей – приведенной формулой).

Таким образом, зарядка конденсатора будет происходить с постоянной времени . Импульс на выходе рассмотреннойRC-цепи приведен на рис.1.36. Как видим, данная цепь с двумя конденсаторами ведет себя как интегрирующая цепочка (сравните рис.1.36 и рис.1.37).

Рис.1.36. Импульс на входе и выходе RC-цепи,

представленной на рис.1.35.

Другой примерRC-цепи с двумя конденсаторами приведен на рис.1.37.

Рис.1.37.RC-цепь с двумя конденсаторами.

В данном случае при скачках входного напряжения конденсаторы будут заряжаться через внутреннее сопротивление генератора импульсов. Если мы положим, что генератор входного напряжения идеальный, то его внутреннее сопротивление равно 0. Это значит, что скачок входного напряжения вызовет скачок напряжения на выходе, причем, как это было показано выше: . Затем будет происходить перезаряд конденсаторов: конденсатор С₁ зарядится до напряжения U_Г, а конденсатор С₂ разрядится до нуля, т.е. напряжение на выходе при t→∞ будет стремиться к 0. Постоянную времени перезарядки конденсаторов можно определить, учитывая, что левую клемму конденсатора С₁ через нулевое внутреннее сопротивление входного генератора можно считать присоединенной к общей шине, т.е. конденсаторы С₁ и С₂ включены параллельно. При включении конденсаторов параллельно их емкости суммируются. Отсюда С_ЭКВ=С₁+С₂. Перезаряд конденсаторов будет происходить через включенный параллельно с ними резистор R, т.е. постоянная времени перезаряда конденсаторов будет равна: τ=(С₁+С₂)R. Входной и выходной импульсы приведены на рис.1.38. Как видим, данная цепь с двумя конденсаторами ведет себя как дифференцирующая цепочка (сравните рис.1.38 и 1.31).

Рис.1.38. Входной и выходной импульсы цепи,

приведенной на рис.1.37.

РассмотримRC-цепь, включающую два резистора и два конденсатора (рис.1.39).

Рис.1.39. RC-цепь, содержащая два резистора

и два конденсатора.

Предположим, на вход цепи подан прямоугольный импульс с амплитудой . В момент положительного скачка входного напряжения конденсатор С₂ зарядится до напряжения . В последующее время будет происходить перезаряд конденсаторов с постоянной времени τ=(С₁+С₂)R₁R₂/(R₁+R₂) (конденсаторы и резисторы при перезарядке конденсаторов будут включены параллельно). При t=∞ напряжение на выходе будет стремиться к (конденсаторы приt=∞ не будут влиять на падение напряжения на резисторах). В зависимости от того, какое напряжение U_ВЫХ(0) или U_ВЫХ(∞) больше, возможна различная форма выходного импульса. При U_ВЫХ(0)>U_ВЫХ(∞) на выходе будет выходной импульс, форма которого приведена на рис.1.40б. При U_ВЫХ(0)<U_ВЫХ(∞) на выходе будет выходной импульс, форма которого приведена на рис.1.40в. При U_ВЫХ(0)=U_ВЫХ(∞) или иR₁C₁=R₂C₂ форма выходного импульса будет прямоугольной (рис.1.40г). Такой емкостный делитель называют компенсированным. Его часто используют в электронных цепях.

Особенно полезен такой компенсированный делитель становится в том случае, если с выхода некой цепи необходимо передать импульс на вход другой цепи без искажения его формы. При этом для идеальной передачи формы импульса необходимо точно знать или рассчитать и выбрать значения сопротивлений резисторов и емкостей конденсаторов.

Рис.1.40. Входной и выходные сигналы цепи,

приведенной на рис.1.39, при различных соотношениях

между сопротивлениями резисторов и емкостями

конденсаторов.