Функция arccos

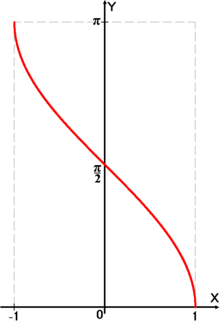
Рис. 10. График функции .

Арккосинусом числа m называется такое значение угла x, для которого

Функция непрерывна и ограничена на всей числовой прямой. Функция является строго убывающей.

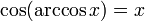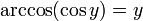• при

• при

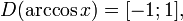• (область определения),

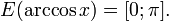• (область значений).

Свойства функции arccos

• (функция центрально-симметрична относительно точки 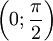), является индифферентной.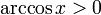

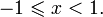
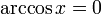• при

• при

• 

• 

• 

• 

• 

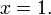
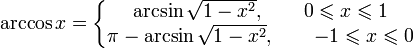
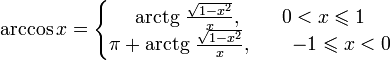
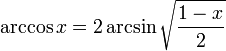
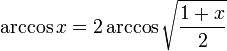
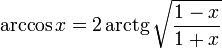
Получение функции arccos

Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — На этом отрезке строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке существует обратная функция график которой симметричен графику на отрезке относительно прямой

Функция arctg

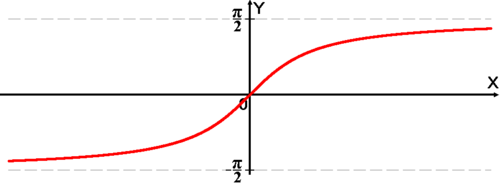
Рис. 11. График функции .

Арктангенсом числа m называется такое значение угла , для которого

Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.

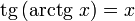• при

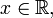
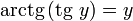• при

• 

• 

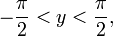
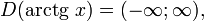
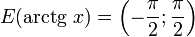
Свойства функции arctg

• 

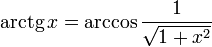• , при x > 0.

Получение функции arctg

Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — На этом отрезке строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале существует обратная , график которой симметричен графику на отрезке относительно прямой

Функция arcctg

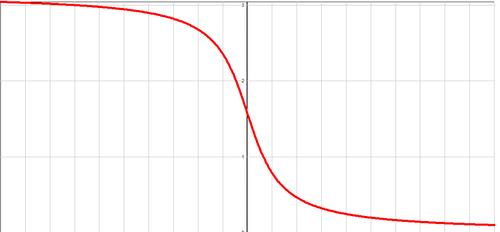
Рис. 12. График функции y=arcctg x

Арккотангенсом числа m называется такое значение угла x, для которого

Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго убывающей.

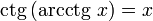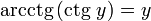• при

• при

• 

• 

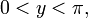
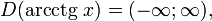
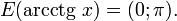
Свойства функции arcctg

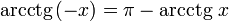• (график функции центрально-симметричен относительно точки

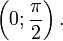
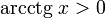• при любых

• 

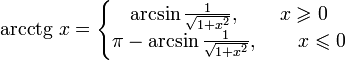
Получение функции arcctg

Дана функция . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим отрезок, на котором она строго убывает и принимает все свои значения только один раз — . На этом отрезке строго убывает и принимает все свои значения только один раз, следовательно, на интервале существует обратная функция , график которой симметричен графику на отрезке относительно прямой График симметричен к арктангенсу

Функция arcsec

Функция arccosec

Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.

Определение

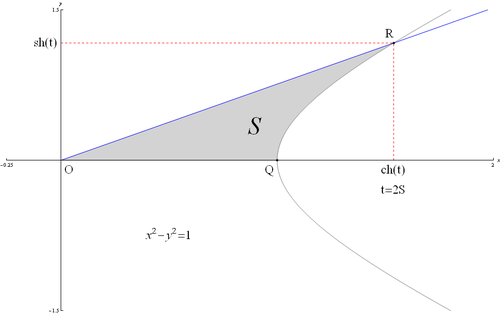
Определение гиперболических функций через гиперболу

Гиперболические функции задаются следующими формулами:

• гиперболический синус:

(в англоязычной литературе обозначается )

• гиперболический косинус:

(в англоязычной литературе обозначается )

• гиперболический тангенс:

(в англоязычной литературе обозначается )

• гиперболический котангенс (в англоязычной литературе обозначается coth (x)):

Иногда также определяются

• гиперболические секанс и косеканс: