Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:
алгебраические:
степенная;
рациональная.
трансцендентные:
показательная и логарифмическая;
тригонометрические и обратные тригонометрические.
Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения.
Иногда к основным элементарным функциям относят также гиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции.
Область определения
Если показатель степени —
целое
число, то можно
рассматривать степенную функцию на
всей числовой
прямой (кроме,
возможно, нуля). В общем случае степенная
функция определена при
.
Если
,
то функция определена также и при
,
иначе нуль является её особой точкой.
Рациональный показатель степени
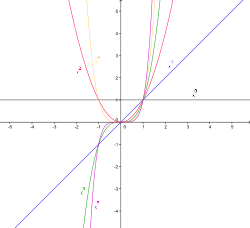
Графики степенной функции при натуральном показателе n называются параболами порядка n. При
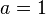получается функция
,
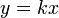называемая прямой
пропорциональной зависимостью.Графики функций вида
,
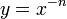где n
— натуральное число, называются
гиперболами
порядка n.
При
получается функция
,
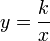называемая обратной
пропорциональной зависимостью.Если
,
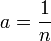то функция есть
арифметический
корень степени
n.
Пример: из
третьего
закона Кеплера
вытекает, что период
T
обращения планеты вокруг
Солнца связан с большой полуосью
A её
орбиты соотношением:
(полукубическая
парабола).
Рис. 1
Параболы
порядка n:
;
;
;
;
;
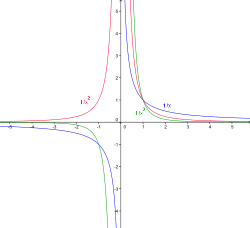
Рис. 2.
Гиперболы порядка
n:
;
;
Свойства
Функция непрерывна и дифференцируема во всех точках, в окрестности которых она определена. Нуль, вообще говоря, является особой точкой; например, функция
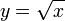определена в нуле и его
правой окрестности, но её производная
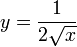в нуле не определена.В интервале
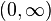функция монотонно
возрастает при
и монотонно убывает
при
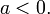Значения функции в этом
интервале положительны.
Рациональная функция — это дробь, числителем и знаменателем которой являются многочлены. Она имеет вид
где
,
— многочлены
от любого числа переменных.
Частным случаем являются рациональные функции одного переменного:
,
где P(x) и Q(x) — многочлены.
Другим частным случаем является отношение двух линейных функций — дробно-линейная функция.
Свойства
Любое выражение, которое можно получить из переменных
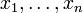с помощью четырёх
арифметических действий, является
рациональной функцией.Множество рациональных функций замкнуто относительно арифметических действий и операции композиции.
Любая рациональная функция может быть представлена в виде суммы простейших дробей (см. Метод неопределённых коэффициентов), это применяется при аналитическом интегрировании.
Правильные дроби
Различают правильные и неправильные рациональные дроби, по аналогии с обычными числовыми дробями. Рациональная дробь называется правильной, если порядок знаменателя больше порядка числителя, и неправильной, если наоборот.
Любую неправильную рациональную дробь можно преобразовать в сумму некоторого многочлена и правильной рациональной дроби
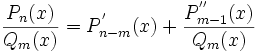
Любую рациональную дробь
многочленов с вещественными коэффициентами
можно представить как сумму рациональных
дробей, знаменателями которых являются
выражения
(a — вещественный корень
Q(x)) либо
(где
не имеет действительных
корней), причём степени k не больше
кратности соответствующих корней в
многочлене Q(x). На основании этого
утверждения основана теорема об
интегрируемости рациональной дроби.
Согласно ей, любая рациональная дробь
может быть интегрирована в элементарных
функциях, что делает класс рациональных
дробей весьма важным в математическом
анализе.
Возведение
в степень
—
бинарная
операция,
первоначально происходящая из
многократного умножения
натурального
числа
на
самого себя. Обозначение:
называется
степенью
с
основанием
и
показателем
.