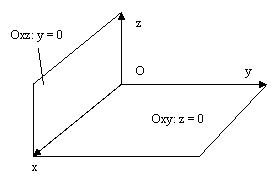40. Пучки параллельных и пересекающихся плоскостей.

Пучок плоскостей  Если

есть ось пучка, то уравнение пучка

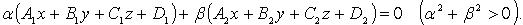
Определение. Пучком плоскостей называется множество всех плоскостей пересекающихся по одной и той же прямой, называемой осью пучка.

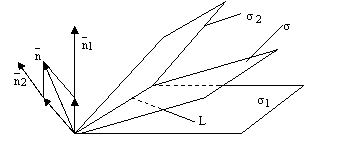
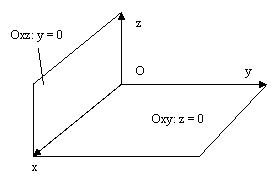
рис.3.

Теорема. Пусть

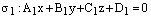 и 

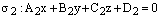
– две плоскости, пересекающиеся по прямой L. Тогда уравнение

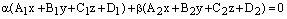,    (10)

где 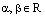  – произвольные действительные числа одновременно не равные нулю, есть уравнение пучка плоскостей с осью пучка L.

Пример. Найти уравнение пучка плоскостей, осью которого является ось абсцисс.

Решение. Очевидно, что координатные плоскост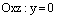и

 и 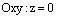  пересекаются по оси Ох.

Тогда уравнение (10) в данном случае принимает вид 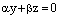. Заменив греческие буквы на латинские, получаем 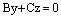, (11) где 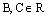  – произвольные действительные числа, одновременно не равные нулю. Уравнение (11) есть искомое уравнение пучка плоскостей с осью пучка Ох.

Аналогично, уравнение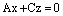 , (12) есть уравнение пучка плоскостей с осью пучка Оу, а уравнение (13) есть уравнение пучка плоскостей с осью пучка Оz.